Расчет потерь в полосе пропускания.

Потери в полосе пропускания фильтра можно рассчитать по формуле [4]

где -параметры прототипа, -затухание в i-ой линии , Q_i-добротность i-ой линии.

Считая резонаторы фильтра одинаковыми, можно потери рассчитать по формуле:

(2.12)

где , а добротность Q микрополосковой линии определяется потерями в проводниках Q_c и потерями в диэлектрике Q_d, то есть:

, откуда

Величину Q_c для полосковой линии с медными проводниками можно определить по формуле:

где b-поперечный размер резонатора (рис2.5б), см;

f- частота настройки фильтра, ГГц;

-находится из графика рис.2.8 [2];

t и -толщина полоски и волновое сопротивление соответственно.

Потери в диэлектрике оцениваются по формуле:

где находится из таблицы 2.3.

Потери на излучение снижают добротность резонатора, поэтому для несимметричной микрополосковой линии добротность вычисляют по формуле:

, где , а затухание d в выражении (2.12) берут равным .



Рис.2.8

Пример 2.1.

Рассчитать полосовой фильтр преселектора приемника по следующим исходным данным:

• средняя частота настройки приемника =1,2 ГГц

• полоса пропускания приемника 10 МГц

• промежуточная частота 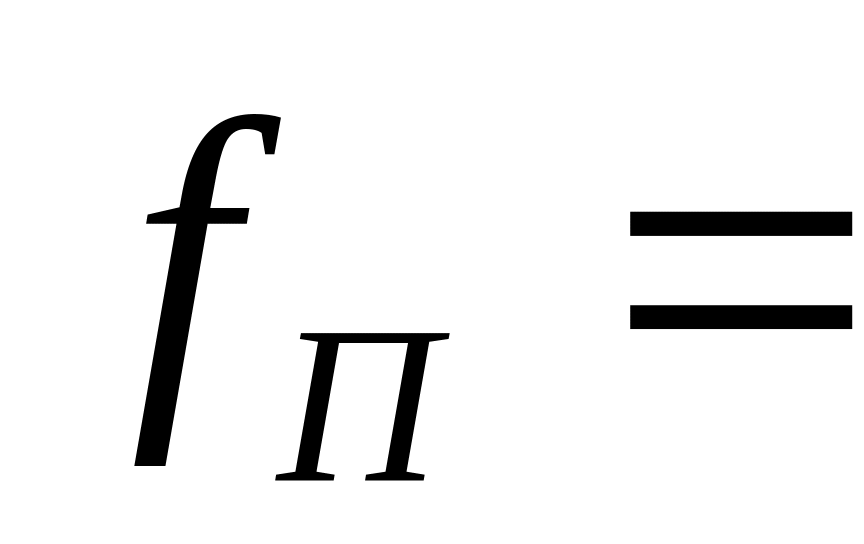60 МГц

• ослабление зеркального канала приемника 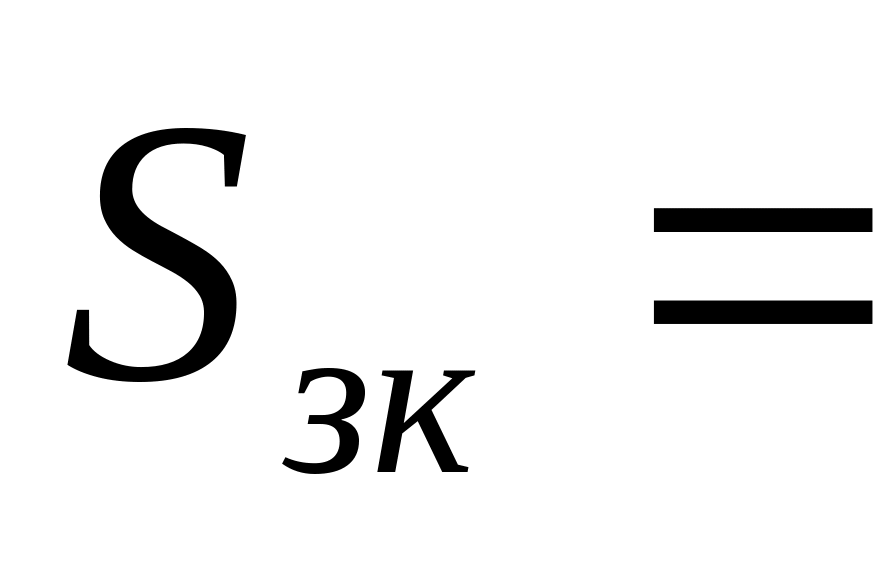60 дБ

На входе и выходе фильтр должен быть согласован с трактом с волновым сопротивлением 50 Ом. Габариты фильтра должны быть минимальны.

1. Ввиду того, что фильтр применяется в приемнике СВЧ, работающем в длинноволновой части дециметрового диапазона волн для сокращения габаритов фильтра используем для его построения четвертьволновые резонаторы и гребенчатую структуру.

2. Поскольку требования к подавлению зеркального канала высокие выберем чебышевскую аппроксимацию характеристики затухания.

3. Зеркальный канал приемника расположен на частоте :

Поэтому полоса запирания фильтра равна:

МГц.

4. В соответствии с заданием полоса пропускания приемника, определяемая фильтрами УПЧ равна 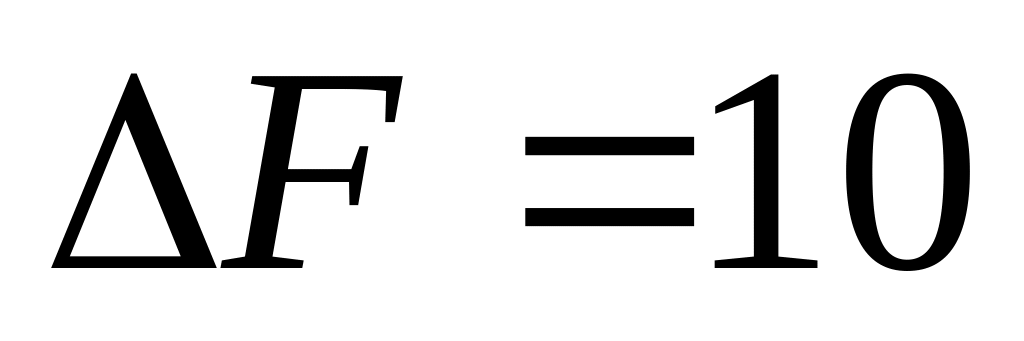МГц, выберем полосу пропускания преселектора 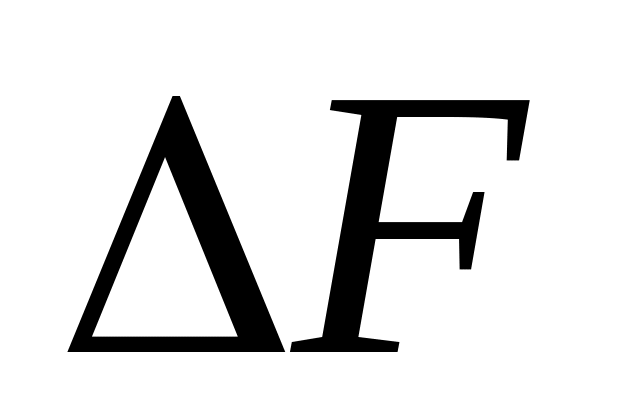в несколько раз больше т.е.:

МГц

5. Находим отношение:

Из графиков рис.2.3 находим, что для подавления зеркального канала, равного L=60дБ, фильтр преселектора должен состоять из n=4 звеньев (резонаторов) при пульсациях на вершине характеристики 1дБ.

Если преселектор приемника состоит из входной цепи и УВЧ целесообразно заданную избирательность по зеркальному каналу поделить поровну между входной цепью и УВЧ т.е. по 30 дБ. Тогда по тем же графикам находим, что фильтр СВЧ должен быть более чем второго класса. Берем n=3. Для реализации выберем микрополосковую несимметричную линию передачи на поликоре с =9,8.

6. Рассчитаем электрические характеристики фильтра при n=3.

Согласно заданию: Ом

Электрическую длину резонатора берем

Волновое сопротивление резонаторов фильтра берем Ом

По формуле (2.7) определяем эффективную диэлектрическую постоянную:

Параметры прототипа находим из таблицы 2.2.

g₀=1; g₁=2,02; g₂=0,99; g₃=2,02; g₄=1.

Из выражения (2.4) получаем

Из формулы (2.5) находим промежуточные параметры:

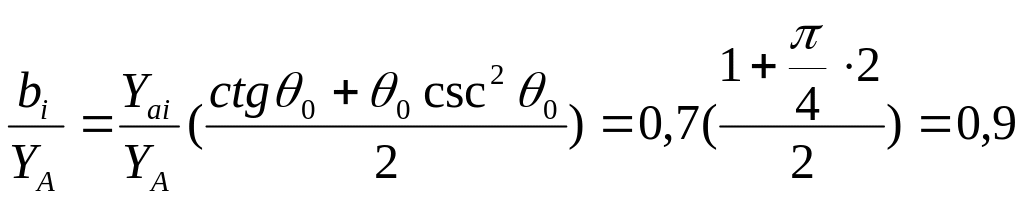
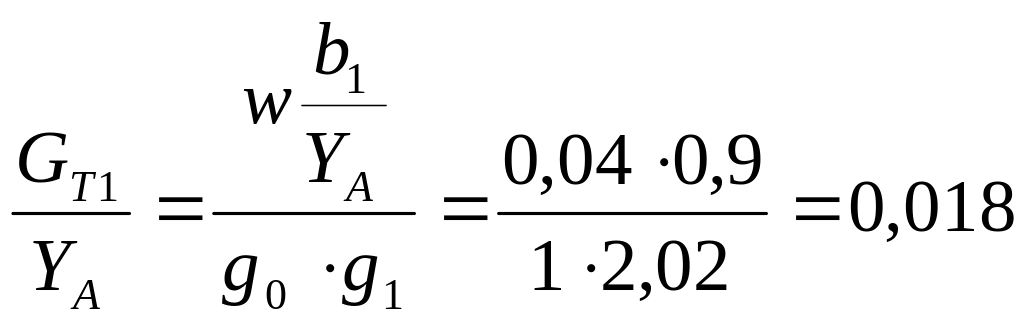
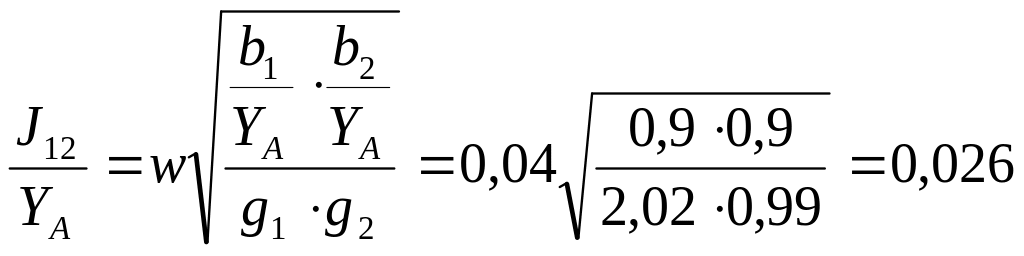
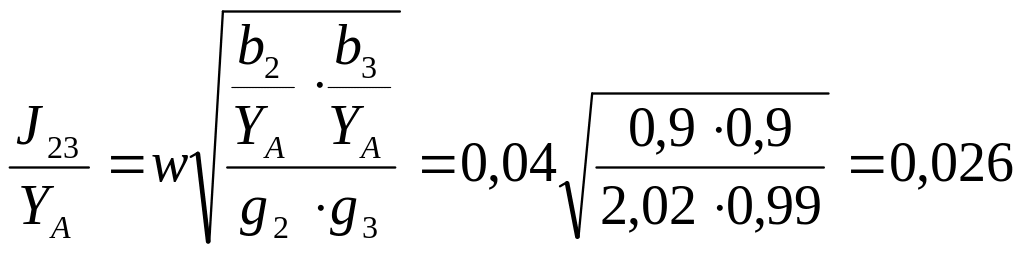
Находим нормированные емкости на единицу длины линии по формулам (2.1):

Находим нормированные взаимные емкости между линиями по формулам (2.2):

Сосредоточенные емкости на концах линий находим по формуле (2.3):

пФ

1. Задаемся поперечным размером фильтра b=10мм и

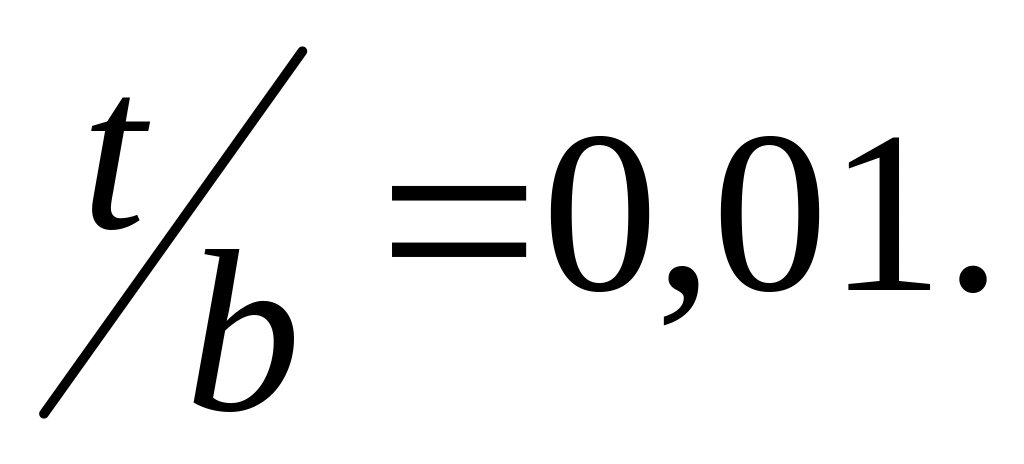
Расстояние S_i,+1 между полосками фильтра находим из графика рис.2.6 и рассчитанным взаимным емкостям :

мм мм мм мм

Ширину полосок рассчитываем по формулам 2.9 2.11:

мм; мм; мм; мм; мм.

Уточненное значение эффективной диэлектрической проницаемости по формуле (2.8) дает Длину резонаторов находим по формуле (2.6):

мм

4. Рассчитаем потери фильтра в полосе пропускания. Расчет по формуле (2.12) производим в следующем порядке. Определяем потери в проводниках:

Потери в диэлектрике находим по формуле:

Параметры прототипа g_i даны в п.6.

Расчет потерь по формуле (2.12) дает:

дБ

4. Эскиз фильтра показан на рис. 2.9

С₁

С₂

С₃

0,01

10

5

1

9

9

1

5

2,4

2,4

1,25

ВхА

ВыхВ

14

Рис. 2.9.