Примечание
При численных расчетах полезно запомнить следующие соотношения
1 неп = 8,68 дБ
1 дБ = 0,115 неп
ln a = 2.3 . lg a
Пример 3.1.
Рассчитать полосовой фильтр на частоту 8 МГц с полосой пропускания 20 кГц. Ослабление на частоте 8,1 МГц должно быть не менее 40 дБ. Сопротивление нагрузки RН = 10 кОм. Фильтр должен иметь стабильные характеристики в диапазоне температур –60о С +85о С.
1. Выбор схемы фильтра
Полоса пропускания фильтра: = fa – fB = 20 кГц.
Средняя
частота настройки фильтра:
МГц
Относительная
полоса пропускания фильтра
равна:
Учитывая узкую полосу пропускания, высокую избирательность и стабильность характеристик, выбираем мостовую схему фильтра с пьезоэлектрическим резонатором в одном плече и конденсатором в другом. Пьезоэлектрический резонатор выполнен на кварцевой пластине АТсреза с колебаниями сдвига по толщине.
2. Расчет параметров фильтра
Выбираем фильтр без полюсов затухания: С01 = С02 и m = 1.
Характеристическое сопротивление фильтра Zm берем равным сопротивлению нагрузки Rн , т.е. Zm = 1 кОм
по формуле (3.6.) находим нормированную расстройку на частоте fH = 8,1 МГц:
По формуле (3.7) определяем ослабление частоты fH в однозвенном фильтре
неп
20 дБ
Итак, однозвенный фильтр не обеспечивает заданных требований по ослаблению частоты fH на 40 дБ.
Двухзвенный фильтр (3.8) дает:
неп
46 дБ
что соответсвует требованиям с запасом.
Потери на средней частоте полосы пропускания определяем по формуле (3.9)
неп = 0,4 дБ
где
таким образом, для обеспечения заданной избирательности необходим двухзвенный фильтр.
Воспользуемся формулами (3.4). Поскольку выбран фильтр с полюсом затухания на частоте f , то
;
пФ
Параметры кварцевого резонатора
пФ
Гн
МГц
3. Расчет параметров кварцевой пластинки АТ - среза находим, пользуясь таблицей 3.1.
Толщина пластинки
см
площадь кварцевой пластинки
см2
параллельная емкость резонатора
пФ
Поскольку С01 = С02 Ср дополнительного конденсатора в цепи резонатора не требуется.
Электрическая схема двухзвенного мостового фильтра показана на рис. 3.9
Р
ис.
3.9
На схеме (рис. 3.9) все пьезоэлектрические резонаторы должны быть одинаковыми и соответствовать рассчитанным параметрам. Конденсаторы в противоположных плечах моста С1 С4 также одинаковы и равны Сi = Сp = 2 пФ.
3.4. Мостовая схема с резонатором в каждом плече.
Улучшить фильтрующие свойства схемы можно в мостовой схеме фильтра с резонатором в каждом плече рис.3.10а.
a) б)
Рис. 3.10
на рис.3.10б показана эквивалентная электрическая схема (симметричная часть схемы не показана).
На рис.3.10 обозначено :
Пэi (i = 1 4) – пьезоэлектрический резонатор с параметрами Lsi и Csi
,
(i
= 1
4)
где
Сpi (i = 1 4) – статическая емкость резонатора ;
СНi (i = 1 4) – емкость добавочного конденсатора.
При симметричном расположении полюсов затухания относительно средней частоты полосы пропускания фильтра формулы для расчета элементов фильтра имеет вид:
;
;
;
;
;
; (3.10)
;
;
где ; ;
;
;
;
.
Фильтр эквивалентен по характеристикам двухзвенному мостовому фильтру рассмотренному ранее. Рабочее затухание рассчитывается по формуле (3.8) , потери на средней частоте полосы пропускания определяются по формуле (3.9)
На рис.3.11 приведены характеристики рабочего затухания двухзвенного фильтра с резонатором в каждом плече при
и
;
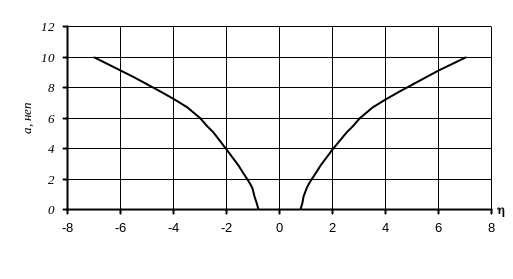
Рис. 3.11
При использовании катушек индуктивности (рис3.12) можно расширить полосу пропускания фильтра до 8% 5
Рис. 3.12
Лестничная схема пьезоэлектрического фильтра (рис3.4) проще мостовой т.к. допускает использование одного резонатора. Лестничные схемы приводятся к эквивалентным мостовым схемам и рассчитываются по аналогичным формулам 5. Однако в следствии узкополосности лестничные схемы применяются реже мостовых.