2 Приведение квадратичной формы к нормальному виду. Метод Лагранжа.
http://sci.alnam.ru/book_alin.php?id=36
http://spargalki.ru/mathematiks/210-lineinaya-algebra.html?start=9
Постановка задачи. Привести квадратичную форму
к каноническому виду методом Лагранжа.
План решения.
Метод
Лагранжа заключается в последовательном
выделении полных квадратов. Не ограничивая
общности рассуждений, полагаем, что
.
где
–
квадратичная форма, в которую входят
лишь переменные
.
Делаем замену
,
после которой
,
где
.
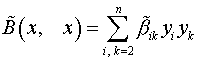Предложенный алгоритм применяем к и после конечного числа шагов приходим к каноническому виду квадратичной формы:
.
Задача 10. Привести квадратичную форму к каноническому виду методом Лагранжа
.
Применяя метод Лагранжа, получаем:
где
.
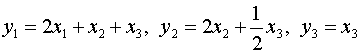ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 8
1. Общее решение неоднородной системы линейных уравнений.
http://matworld.ru/calculator/non-homogeneous-system-online.php
http://www.cleverstudents.ru/systems/solving_systems_of_linear_equations.html#fundamental_system_of_solutions
2. Критерий Сильвестра положительной определенности квадратичной формы.
http://www.studfiles.ru/preview/3072512/page:4/
Критерий Сильвестра
Тип квадратичной формы можно определить, не приводя ее к каноническому виду. Следующий ниже критерий Сильвестра позволяет определить тип квадратичной формы по знакам угловых миноров ее матрицы.
Рассмотрим
угловые миноры 
(
),
являющиеся определителями
подматриц 
матрицы 
квадратичной
формы:
Теорема
6 (критерий
Сильвестра знакоопределенности
квадратичной формы). Квадратичная
форма 
является:
1)
положительно определенной тогда и
только тогда, когда все угловые
миноры 
матрицы
положительны:
(
)
2) отрицательно определенной тогда и только тогда, когда все угловые миноры матрицы отличны от нуля и их знаки чередуются, начиная со знака минус:
В заключение приведем таблицу оценки знакоопределенности квадратичных форм по двум основным критериям.
Квадратичная форма |
Обозна- чение |
Оценка знакоопределенности формы |
|
по главным минорам матрицы квадратичной формы |
по собственным значениям матрицы квадратичной формы |
||
положительно определенная |
|
если все угловые миноры матрицы положительны: ( ) |
если все собственные значения положительны |
отрицательно определенная |
|
если все угловые миноры матрицы отличны от нуля и их знаки чередуются, начиная со знака минус:
|
если все собственные значения отрицательны |
неотрицательно определенная |
|
если
все угловые миноры
матрицы
неотрицательны: |
если все собственные значения неотрицательны |
неположительно определенная |
|
если в угловых минорах матрицы чередуются знаки, причем:
|
если все собственные значения неположительны |
знакопеременная |
|
|
среди собственных значений имеются как положительные, так и отрицательные |
(
)
Пример 6. Исследовать на знакоопределенность следующие квадратичные формы от двух переменных
, 
,
, 
.
Решение.
1) Матрица формы имеет вид
.
Ее угловые миноры равны
, 
.
Согласно
критерию Сильвестра, так как все угловые
миноры положительны, квадратичная
форма 
являетсяположительно
определенной.
2) Матрица формы имеет вид
.
Ее угловые миноры равны
, 
.
Согласно
критерию Сильвестра, так как все угловые
миноры матрицы отличны от нуля и их
знаки чередуются, начиная со знака
минус, то квадратичная
форма 
являетсяотрицательно определенной.
3) Матрица формы имеет вид
.
Ее угловые миноры равны
, 
.
Так
как в этом случае второй угловой минор
отрицателен, то согласно таблице
квадратичная форма 
являетсязнакопеременной.
4) Матрица формы имеет вид
.
Ее угловые миноры равны
, 
.
Так
первый угловой минор положителен, а
второй угловой минор равен нулю, то
согласно таблице квадратичная
форма 
являетсянеотрицательно
определенной.
Заметим, что в данном случае
.
Пример 7. Исследовать на знакоопределенность квадратичную форму от трех переменных
.
Решение. Матрица формы имеет вид
.
Ее угловые миноры положительны:
, 
,
.
Согласно критерию Сильвестра, так как все угловые миноры положительны, то квадратичная форма является положительно определенной.