Оглавление

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 1 3

1. Элементарные преобразования строк матиц. Примеры. 3

2. Евклидовы пространства. Скалярное произведение векторов, длина (норма) вектора, их свойства. 5

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 2 6

1. Применение элементарных преобразований для нахождения обратных матриц и для решения матричных уравнений. 6

2. Неравенство Коши-Буняковского для векторов евклидова пространства. 10

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 3 12

1. Правило Крамера для решения систем линейных уравнений. 12

2 Неравенство треугольника для векторов евклидова пространства. 13

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 4 15

1. Ранг матрицы. Линейная зависимость векторов. 15

2. Ортонормированный базис. Процесс ортогонализации базиса. 17

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 5 21

1. Теорема о базисном миноре. 21

2 Билинейные формы и их свойства. 22

Свойства билинейных форм 22

Преобразование матрицы билинейной формы при переходе к новому базису. Ранг билинейной формы 23

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 6 24

1. Метод Гаусса решения систем линейных уравнений. 24

2. Квадратичные формы и их свойства. Полярные билинейные формы. 27

Приведение квадратичной формы к каноническому виду 28

Закон инерции квадратичных форм 32

Классификация квадратичных форм 33

Необходимое и достаточное условие знакоопределенности квадратичной формы 33

Необходимое и достаточное условие знакопеременности квадратичной формы 33

Необходимое и достаточное условие квазизнакопеременности квадратичной формы 33

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 7 34

1. Фундаментальная система решений однородной системы линейных уравнений. 34

Что такое однородная система линейных уравнений? 34

Фундаментальная система решений однородной системы уравнений 36

Взаимосвязь решений неоднородной  и соответствующей однородной системы уравнений 38

2 Приведение квадратичной формы к нормальному виду. Метод Лагранжа. 44

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 8 46

1. Общее решение неоднородной системы линейных уравнений. 46

2. Критерий Сильвестра положительной определенности квадратичной формы. 46

Критерий Сильвестра 46

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 9 50

1. Линейные пространства. Базис. Размерность. 50

2 Преобразование матрицы билинейной формы при смене базиса. 50

3. Изменение матрицы билинейной (полуторалинейной) формы при изменении базиса. 50

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 10 52

1. Подпространства линейного пространства. Свойства. Сумма и пересечение подпростанств. 52

2 .Собственные векторы и собственные значения линейного оператора. 54

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 11 57

1. Переход к новому базсу в линейном пространстве. Матрица перехода. 57

http://www.studfiles.ru/preview/6144772/page:3/ 57

Переход к новому базису 57

2 Длина вектора и угол между векторами в евклидовом пространстве. 59

Длина вектора и угол между векторами в евклидовом пространстве 59

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 12 64

1. Определение линейного оператора и его свойства. 64

2. Теорема Кронекера-Капелли. 71

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 13 75

1. Образ и ядро линейного оператора в линейном пространстве. 75

2 Решение неоднородных систем линейных уравнений. Представление общего решения в векторной форме. 77

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 14 78

1. Матрица линейного оператора и ее свойства. 78

2. Системы линейных алгебраических уравнений (СЛАУ). Основные понятия. 79

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 15 83

1. Преобразование матрицы линейного оператора при смене базиса. 83

2. Построение фундаментальной системы решений и общего решения однородной системы линейных уравнений. 84

Фундаментальная система решений (конкретный пример) 84

Как найти фундаментальную систему решений линейного уравнения? 84

Какие именно векторы создают фундаментальную систему решений данной системы уравнений? 87

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 16 88

1. Действия над матрицами. Обратная матрица. Матричные уравнения. 88

Обратная матрица 88

Алгоритм нахождения обратной матрицы 88

Решение матричных уравнений 89

2 Ортогональные операторы в евклидовом пространстве. Их свойства. 90

Экзаменационный билет № 1

1. Элементарные преобразования строк матиц. Примеры.

Элементарными преобразованиями матрицы назовем следующие преобразования:

 1) умножение строки на число, отличное от нуля;

  2) прибавление к одной строке другой строки;

  3) перестановка строк;  

4) вычеркивание (удаление) одной из одинаковых строк (столбцов);

  5) транспонирование; Те же операции, применяемые для столбцов, также называются элементарными преобразованиями. С помощью элементарных преобразований можно к какой-либо строке или столбцу прибавить линейную комбинацию остальных строк ( столбцов ).  

Миноры. Выше было использовано понятие дополнительного минора матрицы.

Определение. Если в матрице А выделить несколько произвольных строк и столько же произвольных столбцов, то определитель, составленный из элементов, расположенных на пересечении этих строк и столбцов называется минором матрицы А. Если выделено s строк и столбцов, то полученный минор называется минором порядка s.   Заметим, что вышесказанное применимо не только к квадратным матрицам, но и к прямоугольным.  Если вычеркнуть из исходной квадратной матрицы А выделенные строки и столбцы, то определитель полученной матрицы будет являться дополнительным минором.

Алгебраические дополнения.

Определение. Алгебраическим дополнением минора матрицы называется его дополнительный минор

, умноженный на (-1) в степени, равной сумме номеров строк и номеров столбцов минора матрицы. В частном случае, алгебраическим дополнением элемента матрицы называется его минор, взятый со своим знаком, если сумма номеров столбца и строки, на которых стоит элемент, есть число четное и с противоположным знаком, если нечетное.  

Теорема Лапласа. Если выбрано s строк матрицы с номерами i₁, … ,i_s, то определитель этой матрицы равен сумме произведений всех миноров, расположенных в выбранных строках на их алгебраические дополнения.

Обратная матрица. Определим операцию деления матриц как операцию, обратную умножению.

 Определение. Если существуют квадратные матрицы Х и А, удовлетворяющие условию: XA = AX = E, где Е - единичная матрица того же самого порядка, то матрица Х называется обратной к матрице А и обозначается А^-1.  Каждая квадратная матрица с определителем, не равным нулю имеет обратную матрицу и притом только одну.   Рассмотрим общий подход к нахождению обратной матрицы. Исходя из определения произведения матриц, можно записать: AX = E   , i=(1,n), j=(1,n), e_ij = 0, i  j, e_ij = 1, i = j . Таким образом, получаем систему уравнений:  , Решив эту систему, находим элементы матрицы Х.

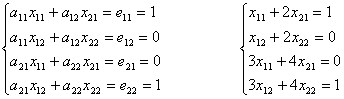
  Пример. Дана матрица А =  , найти А^-1.   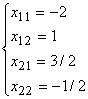    Таким образом, А^-1= . Однако, такой способ не удобен при нахождении обратных матриц больших порядков, поэтому обычно применяют следующую формулу:  , где М_ji- дополнительный минор элемента а_jiматрицы А.

 Пример. Дана матрица А =  , найти А^-1. det A = 4 - 6 = -2. M₁₁=4; M₁₂= 3; M₂₁= 2; M₂₂=1  x₁₁= -2; x₁₂= 1; x₂₁= 3/2; x₂₂= -1/2 Таким образом, А^-1= .

1) Дифференциальное исчисление создано Ньютоном и Лейбницем сравнительно недавно, в конце XVII столетия. Эпизодически понятие касательной встречалось в работах итальянского математика Н. Тартальи- здесь касательная появилась в ходе изучения вопроса об угле наклона орудия, при котором обеспечивается наибольшая дальность полета снаряда. И. Кеплер рассматривал касательную в ходе решения задачи о наибольшем объеме параллелепипеда, вписанного в шар данного радиуса.