2. Неравенство Коши-Буняковского для векторов евклидова пространства.

http://www.studfiles.ru/preview/5058982/page:2/

Теорема 3.1. Для любых векторов х, у евклидова пространства  справедливо неравенство Коши - Буняковского

(3.1)

При  обе части неравенства (3.1) равны нулю согласно свойству 3.3, значит, неравенство выполняется. Отбрасывая этот очевидный случай, будем считать, что . Для любого действительного числа  , в силу аксиомы г), выполняется неравенство

(3.2)

Преобразуем левую часть неравенства, используя аксиомы и свойства скалярного умножения:

Мы получили квадратный трехчлен относительно параметра  (коэффициент при согласно аксиоме г) ненулевой, так как ,неотрицательный при всех действительных значениях параметра. Следовательно, его дискриминант равен нулю или отрицательный, т.е.

Что и требовалось доказать.

Доказательство неравенства Коши — Буняковского выглядит достаточно просто. Тем не менее это неравенство очень полезное. Применяя его в конкретных евклидовых пространствах, мы получаем некоторые хорошо известные в анализе и алгебре неравенства.

Пример 3.5. В случае линейного арифметического пространства   неравенство Коши — Буняковского трансформируется в неравенство Коши:

В евклидовом пространстве  , скалярное произведение в котором выражается определенным интегралом (см. пример 3.4), неравенство Коши — Буняковского превращается в неравенство Буняковского (называемое также неравенством Шварца):

Экзаменационный билет № 3

1. Правило Крамера для решения систем линейных уравнений.

http://function-x.ru/systems_kramer.html

Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.

Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.

Определение. Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается  (дельта).

Определители 

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

.

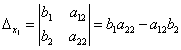Формулы Крамера для нахождения неизвестных:

.

Найти значения   и  возможно только при условии, если

.

Этот вывод следует из следующей теоремы.

Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Пример 1. Решить систему линейных уравнений:

.                         (2)

Согласно теореме Крамера имеем:

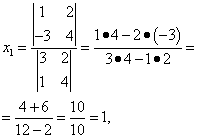
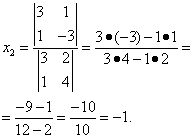
Итак, решение системы (2):