Оглавление

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 1 3

1. Элементарные преобразования строк матиц. Примеры. 3

2. Евклидовы пространства. Скалярное произведение векторов, длина (норма) вектора, их свойства. 5

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 2 6

1. Применение элементарных преобразований для нахождения обратных матриц и для решения матричных уравнений. 6

2. Неравенство Коши-Буняковского для векторов евклидова пространства. 10

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 3 12

1. Правило Крамера для решения систем линейных уравнений. 12

2 Неравенство треугольника для векторов евклидова пространства. 13

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 4 15

1. Ранг матрицы. Линейная зависимость векторов. 15

2. Ортонормированный базис. Процесс ортогонализации базиса. 17

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 5 21

1. Теорема о базисном миноре. 21

2 Билинейные формы и их свойства. 22

Свойства билинейных форм 22

Преобразование матрицы билинейной формы при переходе к новому базису. Ранг билинейной формы 23

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 6 24

1. Метод Гаусса решения систем линейных уравнений. 24

2. Квадратичные формы и их свойства. Полярные билинейные формы. 27

Приведение квадратичной формы к каноническому виду 28

Закон инерции квадратичных форм 32

Классификация квадратичных форм 33

Необходимое и достаточное условие знакоопределенности квадратичной формы 33

Необходимое и достаточное условие знакопеременности квадратичной формы 33

Необходимое и достаточное условие квазизнакопеременности квадратичной формы 33

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 7 34

1. Фундаментальная система решений однородной системы линейных уравнений. 34

Что такое однородная система линейных уравнений? 34

Фундаментальная система решений однородной системы уравнений 36

Взаимосвязь решений неоднородной  и соответствующей однородной системы уравнений 38

2 Приведение квадратичной формы к нормальному виду. Метод Лагранжа. 44

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 8 46

1. Общее решение неоднородной системы линейных уравнений. 46

2. Критерий Сильвестра положительной определенности квадратичной формы. 46

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 9 47

1. Линейные пространства. Базис. Размерность. 47

2 Преобразование матрицы билинейной формы при смене базиса. 47

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 10 48

1. Подпространства линейного пространства. Свойства. Сумма и пересечение подпростанств. 48

2 .Собственные векторы и собственные значения линейного оператора. 48

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 11 49

1. Переход к новому базсу в линейном пространстве. Матрица перехода. 49

2 Длина вектора и угол между векторами в евклидовом пространстве. 49

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 12 50

1. Определение линейного оператора и его свойства. 50

2. Теорема Кронекера-Капелли. 50

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 13 51

1. Образ и ядро линейного оператора в линейном пространстве. 51

2 Решение неоднородных систем линейных уравнений. Представление общего решения в векторной форме. 51

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 14 52

1. Матрица линейного оператора и ее свойства. 52

2. Системы линейных алгебраических уравнений (СЛАУ). Основные понятия. 52

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 15 53

1. Преобразование матрицы линейного оператора при смене базиса. 53

2. Построение фундаментальной системы решений и общего решения однородной системы линейных уравнений. 53

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 16 54

1. Действия над матрицами. Обратная матрица. Матричные уравнения. 54

2 Ортогональные операторы в евклидовом пространстве. Их свойства. 54

Экзаменационный билет № 1

1. Элементарные преобразования строк матиц. Примеры.

Элементарными преобразованиями матрицы назовем следующие преобразования:

 1) умножение строки на число, отличное от нуля;

  2) прибавление к одной строке другой строки;

  3) перестановка строк;  

4) вычеркивание (удаление) одной из одинаковых строк (столбцов);

  5) транспонирование; Те же операции, применяемые для столбцов, также называются элементарными преобразованиями. С помощью элементарных преобразований можно к какой-либо строке или столбцу прибавить линейную комбинацию остальных строк ( столбцов ).  

Миноры. Выше было использовано понятие дополнительного минора матрицы.

Определение. Если в матрице А выделить несколько произвольных строк и столько же произвольных столбцов, то определитель, составленный из элементов, расположенных на пересечении этих строк и столбцов называется минором матрицы А. Если выделено s строк и столбцов, то полученный минор называется минором порядка s.   Заметим, что вышесказанное применимо не только к квадратным матрицам, но и к прямоугольным.  Если вычеркнуть из исходной квадратной матрицы А выделенные строки и столбцы, то определитель полученной матрицы будет являться дополнительным минором.

Алгебраические дополнения.

Определение. Алгебраическим дополнением минора матрицы называется его дополнительный минор

, умноженный на (-1) в степени, равной сумме номеров строк и номеров столбцов минора матрицы. В частном случае, алгебраическим дополнением элемента матрицы называется его минор, взятый со своим знаком, если сумма номеров столбца и строки, на которых стоит элемент, есть число четное и с противоположным знаком, если нечетное.  

Теорема Лапласа. Если выбрано s строк матрицы с номерами i₁, … ,i_s, то определитель этой матрицы равен сумме произведений всех миноров, расположенных в выбранных строках на их алгебраические дополнения.

Обратная матрица. Определим операцию деления матриц как операцию, обратную умножению.

 Определение. Если существуют квадратные матрицы Х и А, удовлетворяющие условию: XA = AX = E, где Е - единичная матрица того же самого порядка, то матрица Х называется обратной к матрице А и обозначается А^-1.  Каждая квадратная матрица с определителем, не равным нулю имеет обратную матрицу и притом только одну.   Рассмотрим общий подход к нахождению обратной матрицы. Исходя из определения произведения матриц, можно записать: AX = E   , i=(1,n), j=(1,n), e_ij = 0, i  j, e_ij = 1, i = j . Таким образом, получаем систему уравнений: 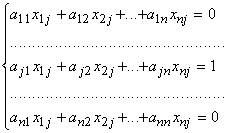 , Решив эту систему, находим элементы матрицы Х.

  Пример. Дана матрица А =  , найти А^-1. 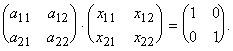      Таким образом, А^-1= . Однако, такой способ не удобен при нахождении обратных матриц больших порядков, поэтому обычно применяют следующую формулу:  , где М_ji- дополнительный минор элемента а_jiматрицы А.

 Пример. Дана матрица А =  , найти А^-1. det A = 4 - 6 = -2. M₁₁=4; M₁₂= 3; M₂₁= 2; M₂₂=1  x₁₁= -2; x₁₂= 1; x₂₁= 3/2; x₂₂= -1/2 Таким образом, А^-1= .

1) Дифференциальное исчисление создано Ньютоном и Лейбницем сравнительно недавно, в конце XVII столетия. Эпизодически понятие касательной встречалось в работах итальянского математика Н. Тартальи- здесь касательная появилась в ходе изучения вопроса об угле наклона орудия, при котором обеспечивается наибольшая дальность полета снаряда. И. Кеплер рассматривал касательную в ходе решения задачи о наибольшем объеме параллелепипеда, вписанного в шар данного радиуса.