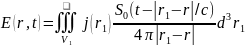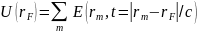2 Метод дифракционного суммирования

Одним из методов получения изображения является миграция. Применение метода является целью изучения структуры среды при наличии только граничных значений различных физических величин на поверхности этой среды. Данная проблема охватывает различные области современной науки и человеческой деятельности, такие как медицина, археология, геофизика, исследование океанов, материаловедение и многие другие [3].

В настоящее время, благодаря, техническому прогрессу и уменьшению стоимости, получили широкое распространение системы подповерхностного зондирования, т.е. георадары. Эти системы позволяют проводить неразрушающие подземные исследования в промышленных целях, таких как поиск потерянных линий связи, контроль состояния труб водо и газоснабжения, обнаружения мин, подземных вод, поиск минеральных ресурсов, а также для археологических и исторических целей, т. е. изучение археологических слоев Земли, поиск различного рода артефактов и т.д. В связи с этим встает вопрос быстрой и качественной обработки данных, которые получены с помощью георадаров [4].

Основным методом обработки данных является миграция. Применение метода миграции осуществляется, если излучение является импульсным. При излучении импульса, форма которого описывается функцией S₀(t), регистрируемый пространственно-временной сигнал записывается как:

(6)

Подобная зависимость асимптотически переходит в гиперболу и поэтому носит название дифракционной гиперболы. В случае распределенных источников наблюдаемое поле приобретает вид суперпозиции множества сдвинутых дифракционных гипербол.

а)	б)
Рисунок 2.1 – Дифракционные гиперболы: горизонтальная ось – координата, вертикальная ось – время

На рисунке 2.1 а показана типичная зависимость этого сигнала от одной из пространственных координат и от времени в случае точечного источника, на рисунке 2.1 б показаны дифракционные гиперболы для случая двух источников.

Соотношение (6) представляет собой решение прямой задачи. Обратная задача, заключающаяся в нахождении распределения источников j(r₁) и может быть решена методом миграции, или суммирования по дифракционным гиперболам. Суть метода заключается в предположении, что каждая наблюдаемая гипербола является проекцией одной точки источника, и все значения сигналов на соответствующей гиперболе нужно просто просуммировать с учетом их временного запаздывания. Необходимо лишь правильно рассчитать эти запаздывания. Получившаяся сумма должна быть сопоставлена с выбранной точкой. Если выбранная точка совпадает с истинным положением источника, то результат даст большее значение сигнала, если нет, то вклад будет незначительным[5].

В нашем случае, если точку фокусировки задать как r_F, то решение методом миграции сводиться к вычислению суммы

Здесь r_m – точки наблюдения поля. Для получения полной картины распределения источников достаточно провести сканирование точкой фокусировки r_F всего интересующего нас пространства. В результате можно записать:

где функция

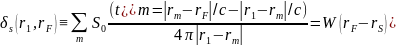
представляет собой аппаратную функцию системы (АФC) – реакцию на точечный источник, которая при достаточно большом размахе и плотном заполнении регистрирующей апертуры начинает зависеть от разности аргументов:

В этом случае соотношение сводиться к интегральной свертке:

Данное уравнение решается стандартным способом, например, с использованием винеровской фильтрации с регуляризацией.

Важно, что при известной форме сигнала S₀(t), вид АФC может быть рассчитан заранее и храниться в памяти вычислительной машины. Тогда для реализации метода миграции становятся применимы быстрые алгоритмы. Обычно при реализации метода миграции АФC подобна “размазанной” δ-функции и ее заменяют на обычную δ-функцию тогда, приближенно записывают, что:

.

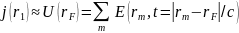Заметим, что получение функции, несмотря на свою внешнюю простоту, требует значительных вычислительных и временных затрат. Достоинством является возможность накопления и уточнения изображения параллельно по мере получения данных измерений [6].

Ниже приведем случаи моделирования обратной задачи.

Рисунок 2.2 – Фокусировка сигнала методом дифракционного суммирования

На рисунке 2.2 изображена фокусировка трех точечных источников.

Рисунок 2.3 – Двумерное изображение фокусировки сигнала

Тоже представление фокусировки представлено на рисунке 2.3.

Рисунок 2.4 – Миграция сигнала (срез Х=2)

На рисунке 2.4 показана фокусировка источника сигнала на расстоянии 3 метров.

Рисунок 2.5 – Миграция сигнала (срез Х=4)

На рисунке 2.5 показана фокусировка источника сигнала на расстоянии 2 метров.

Рисунок 2.6 – Миграция сигнала (срез Х=5)

Из данного рисунка не видно расположения источника, что соответствует действительности.

Рисунок 2.7 – Миграция сигнала (срез Х=6)

На рисунке 2.7 показана фокусировка источника сигнала на расстоянии 1 метра.

Обработка данных проводились с использованием технического языка программирования Matlab на ПК со следующими характеристиками: процессор – Intel® Core™ i5 CPU M430 2,3 ГГц, ОЗУ – 4 Гб. Размер расчетной области составлял 1024x512 точек. Время затраченное на обработку области составило 5,3 секунд.