
Задания для выполнения контрольных работ по дисциплине «методы оптимизации»
Заочное обучение
Задачи линейной оптимизации
Постановка задачи
Рассмотрим модель организации, состоящей из активно взаимодействующих элементов. Можно выделить пять основных элементов – ресурсов.
Кадры.
Информация.
Финансы.
Оборудование
Материалы.
Задача состоит в поиске оптимального, наилучшего варианта, в смысле выбранного критерия, работы организации (задача оптимизации). Определить эффективность решения задачи позволяет так называемая целевая функция.
Эффективность работы организации можно оценить, если в качестве целевой функции W выбрать, например, издержки или прибыль. Издержки следует минимизировать, а прибыль – максимизировать. Тогда функцию цели можно представить
W
= f(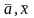 ),
),
где
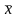 –
вектор факторов,
–
вектор факторов,
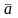 –
вектор внутренних параметров системы,
–
вектор внутренних параметров системы,
при этом должно выполняться условие, накладываемое на целевую функцию
W → opt,
которое представляет собой критерий оптимальности данной задачи.
Пусть W = L – линейная функция, тогда запись opt означает max и min т.е. «наибольшее» и «наименьшее» значения, которые может принимать линейная функция цели на границе допустимого множества факторов.
Область определения функции цели представляет систему ограничений в виде системы уравнений и неравенств.
Если функция цели линейна и ее область определения задана линейной системой, то поставлена задача линейной оптимизации (ЗЛП), относящаяся к линейному классу задач математического программирования.
Пример типовой ЗЛП
Задача о пищевом рационе для столовой
Имеется набор продуктов П1, П2, П3, П4. Их стоимости с1, ..., сn. Диета должна содержать: белков (Б) не менее чем b1, углеводов (У) не менее чем b2, жиров (Ж) не менее чем b3.
Известно, что П1 содержит: а11 белков, а12 углеводов, а13 жиров и т.д.
Найти диету с наименьшей (min) стоимость.
Пусть: xj , (j = 1, ..., 4) – количество продуктов Пj в диете.
-
Продукты
П1
П2
П3
П4
Запасы
Ресурсы
Б
a11
b1
У
a22
b2
Ж
a34
b3
Цены
c1
c2
c3
c4
Стоимость
диеты Д =
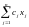 (цель); Д
(цель); Д
 min
min
Ограничения:
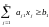 ,
,
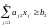 ,
,
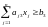
при
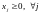 .
.
Требуется найти: неотрицательные значения xj, удовлетворяющие ограничениям, при которых Д стремится к своему наименьшему значению, обозначенному как min.
Подход к решению задачи
Решение этой задачи условно можно разделить на три последовательных этапа.
Формирования информационной постановки задачи, представляющей собой матрицу планирования, составленную на основе семантической (словесно-смысловой) постановки.
Формализация математической модели задачи, состоящей из линейной целевой функции и линейной системы ограничений на варьируемые (изменяемые, искомые) переменные задачи и формулировка критерия оптимальности.
Нахождение оптимального решения задачи (плана), представленного набором (вектором) факторов, на котором функция цели достигает своего наилучшего (по условиям задачи) значения.
Первые два этапа представляют собой процедуру математического моделирования.
Задача приходит к исследователю обычно в семантической форме, описывающей в произвольной форме предметную область, численные характеристики исследуемой системы и пожелания заказчика.
Эту форму задания в общем виде можно описать следующим образом.
После краткого описания, производящей продукт системы, указывается, что для выпуска n – видов продукции используется m – видов ресурсов, при этом расходные коэффициенты: aij – количество единиц i-го ресурса, идущего на изготовления одной единицы j-й продукции, bi – запасы i-го ресурса, cj – цена единицы j-го продукта. Тогда xj – количество единиц j-го продукта, которые необходимого произвести.
В качестве строгой структурированной записи задачи используется её информационная постановка в виде матрицы – представление выдвинутых условий к системе в табличной форме, называемой матрицей планирования.
Таблица 1
Продукты Ресурсы |
Р1 |
Р2 |
… |
Рn |
Запасы |
S1 S2 . . . Sm |
|
|
aij |
|
b1 b2 . . . bm |
Цена единицы продукции |
с1 |
с2 |
… |
cn |
|
Искомое решение |
x1 |
x2 |
… |
xn |
|
Математическая модель задачи формализуется следующим образом.
Рассматриваются 2 основных типа постановок задач линейного программирования.
ОЗЛП можно сформулировать так (первый тип):
максимизировать
W1(x1, …, xm) = λ1x1+ λ 2x2+…+ λ nxn (1)
при условиях:
 (2)
(2)
и дополнительных условиях неотрицательности переменных
x1 ≥0, x2 ≥0, ., xn ≥0. (3)
Второй тип ОЗЛП имеет вид:
минимизировать
W2(x1, …, xm) = λ1x1+ λ 2x2+…+ λ nxn (4)
при условиях:
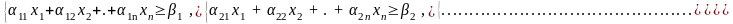 (5)
(5)
при этом дополнительные условия неотрицательности переменных (3) сохраняются.
Если не оговорена неделимость продукции, то xi являются вещественными числами.
Но существует ряд задач, в которых искомые переменные относятся к целочисленному типу. Такие задачи по аналогии отнесены к классу целочисленного линейного программирования.
В общем случае реальные постановки приводят к задачам смешанного типа, сочетающие в системе ограничений различные неравенства и уравнения. Например,
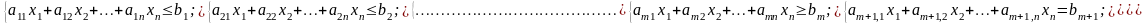 (6)
(6)
Если все ограничения в ЗЛП имеют вид равенств:
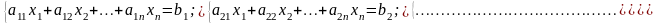 (7)
(7)
то данная форма записи называется канонической (КЗЛП). Функция цели при этом сохраняет вид (1), (4).
Переход к канонической форме (7) осуществляется преобразованием системы ограничений следующим образом. Неравенство
а11x1 + a12x2 +…+ a1mxm ≤ b1
приводится к уравнению добавлением дополнительной неотрицательной переменной, называемой фиктивной, xm+1 ≥ 0 с коэффициентом а1m+1= +1. Если знак неравенства противоположный, то коэффициент при фиктивной переменной равен – 1.
КЗЛП необязательно имеет оптимальное решение. Может оказаться, что оптимальное решение существует, но не на области допустимых значений, или допустимые решения существуют, но среди них нет оптимального. Подобная ситуация часто возникает, если отсутствуют ограничения на целевую функцию сверху или снизу среди уравнений (7).
Вопрос о существовании допустимого решения КЗЛП сводится к исследованию существующего решения, т.е. к вопросу о совместности системы уравнений. Эта проблема решена в линейной алгебре теоремой о ранге матрицы.
Допустимым множеством решений задачи (1)-(3) называется множество R(х) всех векторов x, удовлетворяющих условия (2) и (3). Множество R(х) представляет собой выпуклый многогранник.
Решение x* называется оптимальным, если он удовлетворяет условию:
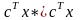 ,
для всех
,
для всех
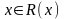
Поскольку поиск min f(х) эквивалентен поиску max[-f(х)], то задачу минимизации в ЛП всегда можно свести к эквивалентной задаче максимизации.
Компактно, в свёрнутой форме, задачу ЛП можно представить как
W(x1,
…, xm)=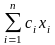
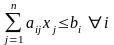
В матричной форме задача ЛП записывается следующим образом:
максимизировать (например)
cTx
при ограничениях:
Ax ≤ b ;
x ≥ 0,
где А - матрица ограничений размером (т x п); b- вектор-столбец свободных членов размером m; x – вектор-столбец переменных размером n; сТ = (c1, c2,...,cn) – вектор-строка коэффициентов целевой функции.
Двойственная задача линейного программирования
С каждой задачей линейного программирования тесно связана другая задача линейного программирования, являющаяся сопряженной к исходной задаче и называется двойственной. При этом решение одной из них может быть непосредственно получено из решения другой.
Рассмотрим это на примере задачи использования ресурсов.
Исходная задача.
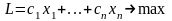 (8)
(8)
 (8а)
(8а)
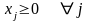
Двойственная задача. оценивает стоимость единиц ресурсов, используемых для производства продукции, (в тех же денежных ед.) yj.. Стоимость всех имеющихся ресурсов будет равна
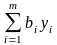 .
Тогда критерием оптимальности будет
.
Тогда критерием оптимальности будет
 (9)
(9)
 (9а)
(9а)
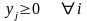
Принято yi называть оценками или учетными, неявными ценами. Имеет смысл говорить о паре двойственных задач линейного программирования. Если решение существует, то minM=maxL.
Двойственная пара задач (8) - (9) представляет собой симметричную пару и является частным случаем двойственности в линейном программировании.
Вычислительный аспект
Математические методы решения задач ЛП входят в состав методов математического программирования. Их особенность заключается в том, чтобы найти оптимум линейной целевой функции, который располагается на границе области определения целевой функции. Более того, оптимальное решение находится в угловой точке многогранника решений, на пересечении рёбер.
Для нахождения оптимальных значений задачи разработан набор специальных методов.
Рассмотрим каноническую задачу линейного программирования (4), (7), (3).
Если число уравнений (7) равно числу переменных (m = n), то решение системы рассматривается в линейной алгебре. Если определитель системы (7) отличен от 0, то система имеет единственное решение. В этом случае критерий никак не влияет на решение.
Если число уравнений системы (7) меньше числа переменных (m < n), то система уравнений имеет бесконечное множество решений, т.е. бесконечное множество векторов . Бесконечное множество решений обеспечивает и требование (3) неотрицательности их значений. Любое из множества неотрицательных решений называется допустимым.
Из множества допустимых решений надо выбрать одно, обеспечивающее минимум целевой функции.
Если ограничения, представленные системой неравенств, имеют решения (хотя бы одно), то эта система называется совместной, а множество точек пространства решений ограниченное этой системой будет выпуклым. Если оно ограниченно и замкнуто, то совокупность точек, представляющих решение системы, будем называть многоугольником решений (на плоскости), т.к. он представляет собой пересечение полуплоскостей (выпуклых множеств). В трехмерном пространстве и пространствах высшей размерности совокупность решений будет представлять собой многогранник решений. В линейном программировании допускается неограниченность допустимой области решений (если это не приводит к неразрешимости задачи) и по аналогии она также называется многогранником.
Т.к. m < n, то одно из возможных решений можно найти, если m - n каких-то переменных положить равными 0. Тогда допустимое решение можно найти, средствами линейной алгебры решая систему m уравнений с m неизвестными. Если определитель системы отличен от 0, то получим ее решение, называемое базисным. n-m переменных являются небазисными, или свободными.
Может существовать множество базисных решений с различными базисными переменными. Если среди значений базисных переменных есть отрицательные, то такие базисные переменными недопустимые. Допустимые базисные решения не содержат отрицательных значений переменных.
Геометрическая интерпретация решения ЗЛП
Рассмотрим на примере геометрическую интерпретацию решения ЗЛП.
Пример.
Дана целевая функция
q’ = x1 – x2
и система ограничений
-2x1 + x2 + x3 = 2
x1 – 2x2 +x4 = 2
x1 + x2 + x5 = 5
xi>=0, i=1,…,5
Найти максимум целевой функции, при учете ограничений.
Имеем n=5 число переменных и m=3 число уравнений: m=3 базисных переменных и n-m=2 свободных переменных. Пусть свободными будут x1 и x2. Выразим через свободные переменные базисные:
x3 = 2x1 – x2 +2
x4 = -x1 + 2x2 + 2
x5 = -x1 – x2 + 5
На плоскости отобразим x1 и x2. Все переменные могут принимать только неотрицательные значения, поэтому рассматриваем 1-ю четверть плоскости.
Теперь построим прямые x3, x4, x5 и учтем ограничения их неотрицательности.
Для x3 проводим прямую и отмечаем штриховкой область, где x3<0, рис. 1.

Рис. 1
Аналогично строим прямые для x4, x5 и штриховкой отмечаем недопустимые области, рис. 2.

Рис. 2
На рис. 2 числа в скобках помечают заштрихованные недопустимые области для соответствующей переменной. В результате допустимой областью для всех переменных стал выпуклый многоугольник 0abcd. Многоугольник является замкнутым и выпуклым, т.к. представляет пересечение выпуклых областей xi>=0.
Т.к. каждая прямая соответствует обращению в 0 одной переменной, то пересечение двух прямых соответствует обращению в 0 двух переменных, т.е. n – m свободных переменных.
Таким образом, точки пересечения прямых соответствуют базисным решениям ЗЛП: вершины многоугольника представляют допустимые базисные решения.
В задаче необходимо найти максимум целевой функции, поэтому из допустимых базисных решений надо выбрать наилучшее. График целевой функции – прямая, направленная под углом 45 град. к оси абсцисс, причем направление увеличения значения q’ показано стрелкой. Прямая должна иметь общие точки с допустимой областью. На рис. 2 видно, что максимальное значение q’ достигается, когда прямая является опорной для допустимых решений (пунктирная линия, проходящая через точку b на рис. 2).
Решение ЗЛП лежит обязательно среди допустимых базисных решений.
Целевая функция в ЗЛП линейна, поэтому ее оптимум глобальный.
Таким образом, геометрически решение задачи линейного программирования представляет собой отыскание оптимального (наибольшее или наименьшее) значения целевой функции. Это решение достигается в точке, принадлежащей многограннику системы ограничений (множеству допустимых решений), опорные плоскости которого называются опорными планами. Опорная плоскость проходит через вершину или ребро так, что многогранник полностью находится только по одну сторону от этой плоскости. Оптимальное решение задачи линейного программирования ищут на множестве опорных планов. При этом оптимальное значение целевой функции достигается в угловой точке многогранника решений.
Оптимум достигается либо в одной крайней точке допустимого множества, либо на множестве крайних точек, а значит на любой выпуклой комбинации этих точек. Это означает, что решение ЗЛП обязательно лежит среди допустимых базисных решений.
Решение ЗЛП с помощью симплекс-метода
Перебирая значения целевой функции в допустимых базисных решениях, можно найти оптимальное. Поскольку перебор оказывается трудоемким, разработаны методы, позволяющие целенаправленно перебирать допустимые решения, сводя их объем к минимуму.
Вначале ищется любое допустимое базисное решение. Для этого выбираются n – m свободных переменных. Ищется решение системы из m уравнений с m неизвестными.
Если решение не допустимое, то выбираются другие свободные переменные и снова ищется решение системы – базисное.
Если базисное решение допустимое, то вычисляется значение целевой функции в нем и делается оценка возможности ее улучшения.
Проверяется достижение оптимума. Если оптимум найден, то получено решение ЗЛП.
Если оптимум не достигнут, то вычисляется новое допустимое базисное решение, но не любое, а лишь то, которое улучшает целевую функцию.
Метод довольно быстро приводит к решению ЗЛП, т.к. перебираются далеко не все допустимые базисные решения.
Рассмотрим предыдущий пример, действуя по указанному сценарию.
В качестве свободных переменных выберем x1 и x2, положив x1 = x2 = 0.
Тогда x3 = 2, x4 = 2, x5 = 5 допустимое базисное решение. Значение целевой функции в нем: q' = 0.
Проверяем, достигнут ли максимум q'. Это можно проверить, взяв другое допустимое базисное решение. Переменная x1 входит в q' со знаком «+», следовательно, ее введение в базис может увеличить q'. Но при этом могут другие базисные переменные могут уменьшаться, соответственно уменьшая q'. Поэтому в свободные переменные надо отправить ту, которая раньше других обратиться в нуль.
Из выражений для x3, x4, x5 видно, что при увеличении x1 уменьшаются x4 и x5, причем в 0 обращается быстрее x4 . Значит, теперь свободной переменной становится x4.
Полагаем x4 = 0, x2 = 0, тогда x1 = 2, x3 = 6, x5 = 3, q' = 2.
Выражаем q' через новые свободные переменные:
q' = 2 +x2 – x4
В целевую функцию входит переменная x2 со знаком «+», т.е. возможно улучшение целевой функции. Поэтому повторяем те же действия: включаем в базис x2 и исключаем ту переменную, которая быстрее обращается в 0, т.е. x5.
Выражаем x1 , x2, x3 через свободные переменные
x1 = 4 - x4/3 – 2x5/3
x2 = 1 + 4x4/3 – x5/3
x3 = 9 – x4 - x5
Получаем q' = 3.
Выражаем q' через новые свободные переменные:
q' = 3 - 2x4/3 – x5/3
При увеличении свободных переменных целевая функция будет уменьшаться, т.о. решение найдено:
x1 = 4 , x2 = 1, x3 = 9, x4 = x5 =0, q' = 3.
Описанный метод достаточно громоздкий из-за постоянных преобразований системы уравнений.
Удобнее использовать симплекс-метод в виде таблицы пересчета решения.
Табличный способ расчетов симплекс-метода
Рассматривается та же ЗЛП.
Дана целевая функция
q’ = x1 – x2
и система ограничений
-2x1 + x2 + x3 = 2
x1 – 2x2 +x4 = 2
x1 + x2 + x5 = 5
xi>=0, i=1,…,5
Найти максимум целевой функции, при учете ограничений.
Построим следующую таблицу.
Таблица 2
Базис |
сБ |
1 |
-1 |
0 |
0 |
0 |
bj |
j |
|||||
x1 |
x2 |
x3 |
x4 |
x5 |
|||||||||
x3 |
0 |
-2 |
1 |
1 |
0 |
0 |
2 |
|
|||||
x4 |
0 |
1 |
-2 |
0 |
1 |
0 |
2 |
2 |
|||||
x5 |
0 |
1 |
1 |
0 |
0 |
1 |
5 |
5 |
|||||
Δi |
-1 |
1 |
0 |
0 |
0 |
|
|||||||
В качестве базисных переменных выбраны x3, x4, x5 – они записаны в первом столбце «Базис».
Начальное решение задачи: x1 = 0, x2 =0, x3 = 2, x4 =2, x5 = 5, q’ = 0.
Столбец сБ содержит коэффициенты целевой функции при базисных переменных. В верхней строке табл. 2 над названиями переменных записываются соответствующие коэффициенты функции цели.
В столбце bj записаны правые части системы уравнений.
В подсвеченной цветом внутренней части таблицы находятся коэффициенты левой части системы уравнений при соответствующих переменных.
Столбец j будет содержать вычисленные оценки для определения базисной переменной (ведущей строки), которую необходимо исключить из базиса, если оптимальное решение еще не найдено.
В нижней строке (красного цвета) под переменными запишем вычисленные коэффициенты Δi, определяющие ведущий столбец – какую переменную надо ввести в новый базис, если не получено оптимальное решение.
Если все коэффициенты Δi в выделенной строке при небазисных переменных неотрицательны, то текущее базисное решение является оптимальным.
В противном случае на следующей итерации в число базисных переменных вводим ту небазисную переменную, для которой коэффициент минимален.
!!!Важное замечание!!! В случае решения задачи на минимум правила для Δi таковы:
- все коэффициенты неположительны - получен оптимальный план;
- среди коэффициентов есть хотя бы одна положительная, и в столбце над ней есть хотя бы один положительный элемент - план неоптимален, возможно его улучшение;
- среди коэффициентов есть хотя бы один положительный, и в столбце над ним нет ни одного положительного элемента - целевая функция не ограничена сверху, оптимального плана не существует.
Коэффициенты Δi вычисляются так:
Δi =( сБ )Т * ai – q’i ,
где сБ - столбец коэффициентов из табл. 2, Т – знак операции транспонирования вектора-столбца в вектор-строку;
ai – столбец коэффициентов системы при xi;
q’i – коэффициент в целевой функции при xi .
Для нашей табл. 2 вычислим коэффициенты Δi
Δ1 = 0*(-2)+0*1+0*1 – 1 =-1, Δ2 = 0*1+0*(-2)+0*1 – (-1) = 1
Получили, что Δ1 <0, что означает неоптимальность полученного решения. Таким образом, ведущим столбцом будет столбец x1, и переменная x1 будет введена в новый базис.
Если в ведущем столбце нет положительных элементов, то решение задачи неограниченно (нет оптимального решения). В противном случае ищется ведущая строка, определяющая, какую «старую» базисную переменную надо заменить на x1.
Для этого вычисляем оценки j как отношение каждого элемента столбца bj к соответствующему элементу ведущего столбца. Если какой-то элемент ведущего столбца меньше или равен 0, то деление не проводится.
2 = 2/1 = 2, 3 = 5/1 =5.
Из j выбирается минимальный положительный. Он показывает ведущую строку. В табл. 2 ведущая строка показывает на x4, следовательно, x4 будет исключаться из нового базиса.
Выделяем желтым цветом ведущий элемент, стоящий на пересечении ведущего столбца и ведущей строки.
Теперь надо построить новую таблицу, пересчитав ее элементы относительно ведущего элемента по методу Гаусса: ведущий элемент должен стать равным 1 (в примере это получилось случайно), остальные элементы ведущего столбца должны равняться 0.
При пересчете действует «правило прямоугольника» относительно ведущего элемента и пересчитываемых элементов. Пересчеты проходят по старой таблице (табл. 2).
Столбец элементов при x1:
((-2)*0-1*0)/1 = 0 , 1/1 = 1, (1*0-1*0)/1 = 0
Столбец элементов при x2:
(1*1-(-2)*(-2))/1 = -3, -2/1 = -2, (1*1-1*(-2))/1 = 3
Столбец элементов при x3: остается без изменений.
Столбец элементов при x4:
(0*1-(-2)*1)/1 = 2, 1/1 = 1, (1*0-1*1)/1 = 0
Столбец элементов при x5: остается без изменений.
Столбец элементов при bj:
(2*1-(-2)*2)/1 = 6, 2/1 = 2, (1*5-1*2)/1 = 3
Теперь формируем новую симплексную таблицу (табл. 3).
Таблица 3
Базис |
сБ |
1 |
-1 |
0 |
0 |
0 |
bj |
j |
|||||
x1 |
x2 |
x3 |
x4 |
x5 |
|||||||||
x3 |
0 |
0 |
-3 |
1 |
2 |
0 |
6 |
|
|||||
x1 |
1 |
1 |
-2 |
0 |
1 |
0 |
2 |
|
|||||
x5 |
0 |
0 |
3 |
0 |
0 |
1 |
3 |
1 |
|||||
Δi |
0 |
-1 |
0 |
1 |
0 |
|
|||||||
Новое решение: x1 = 2, x2 =0 , x3 = 6, x4 = 0, x5 = 3, q’ = 2.
Определяем, оптимально ли полученное решение. Для этого вычисляем Δi.
Δ1 = Δ3 = Δ5 =0, Δ2 = 0*(-3)+1*(-2)+0*3 – (-1) = -1, Δ4 =0*2+1*1+0*1 – 0 =1
Имеем одно Δ2<0, значит, x2 необходимо ввести в новый базис, x2 - ведущий столбец.
Определяем, какую переменную надо исключить из базиса. Вычисляем j = bj/aj2.
1, 2 – не вычисляются, 3 = 3/3=1, т.е. строка x5 ведущая, x5 исключается из базиса. Ведущий элемент выделен желтым цветом.
Рассчитываем новую симплексную таблицу.
Столбец элементов при x1: остается без изменений.
Столбец элементов при x2: 0, 0,1.
Столбец элементов при x3: остается без изменений.
Столбец элементов при x4:
(2*3-0*(-3))/3 = 2, (1*3-0*(-2))/3 = 1, 0/3 = 0
Столбец элементов при x5:
(0*3-1*(-3))/3 = 1, (0*3-1*(-2))/3 = 2/3, 1/3.
Столбец элементов при bj:
(6*3-3*(-3))/3 = 9, (2*3-3*(-2))/3 = 4, 3/3 = 1
Теперь формируем новую симплексную таблицу (табл. 4).
Таблица 4
Базис |
сБ |
1 |
-1 |
0 |
0 |
0 |
bj |
j |
|||||
x1 |
x2 |
x3 |
x4 |
x5 |
|||||||||
x3 |
0 |
0 |
0 |
1 |
2 |
1 |
9 |
|
|||||
x1 |
1 |
1 |
0 |
0 |
1 |
2/3 |
4 |
|
|||||
x2 |
-1 |
0 |
1 |
0 |
0 |
1/3 |
1 |
|
|||||
Δi |
0 |
0 |
0 |
1 |
1/3 |
|
|||||||
Новое решение: x1 = 4, x2 =1 , x3 = 9, x4 = 0, x5 = 0, q’ = 3.
Определяем, оптимально ли полученное решение. Для этого вычисляем Δi.
Δ1 = Δ2 = Δ3 =0, Δ4 = 0*2+1*1+(-1)*0 – 0 = 1, Δ5 =0*1+1*2/3+(-1)*1/3 –0=1/3
Отрицательных Δi нет, поэтому найдено оптимальное решение.
Решение ЗЛП в MS Excel
Проверим решение задачи средствами MS Excel. Построим следующую таблицу.

Рис. 3
Ячейки B6-F6 пока пустые (нулевые значения), после решения ЗЛП в них будет записано решение.
Ячейка B7 содержит формулу вычисления целевой функции.

Рис. 4
Активизируем ячейку B7 и вызовем программу «Поиск решения».

Рис. 5
В окне поиск решения установим все необходимые ссылки на ячейки, укажем, что ищется максимум целевой функции, добавим все необходимые ограничения и нажмем кнопку «Выполнить». В результате будет найдено оптимальное решение.

Рис. 6
