Физика ответы на вопросов .

1.Перемещение , путь , скорость материальной точки .

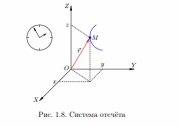
• Траектория — это линия, вдоль которой движется тело. На рис. 1.8 траекторией точки M является синяя дуга, которую описывает в пространстве конец радиус-вектора ~r.

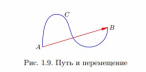
• Путь — это длина участка траектории, пройденного телом за данный промежуток времени.

• Перемещение — это вектор, соединяющий начальное и конечное положение тела.

• Скорость материальной точки представляет собой вектор, характеризующий направление и быстроту перемещения материальной точки относительно тела отсчета.

• Ско́рость  векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки относительно выбранной системы отсчёта; по определению, равна производной радиус-вектора точки по времени. 

Скорость — V Путь — s Время — t

2. Ускорение материальной точки . Тангенциальное и нормальное .

Ускорение – это величина, которая характеризует быстроту изменения скорости.

Ускорение является векторной величиной, показывающей, на сколько изменяется вектор скорости U{\displaystyle {\vec {v}}}  тела при его движении за единицу времени:

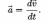
Ускорение материальной точки — векторная физическая величина, характеризующая быстроту изменения скорости и равная приращению скорости за единицу времени. Вектор ускорения равен первой производной от вектора скорости по времени или второй производной от радиуса-вектора по времени.

Тангенциальное ускорение – быстрота изменения скорости по модулю в данный момент времени; производная от скорости по времени.

Нормальное ускорение – быстрота изменения скорости по направлению в данный момент времени.

3. Движение тела , брошенного под углом к горизонту .

Если начальная скорость брошенного тела направлена вверх под некоторым углом к горизонту, то в начальный момент тело имеет составляющие начальной скорости как в горизонтальном, так и в вертикальном направлениях .  Движение тела, брошенного под углом к горизонту или в горизонтальном направлении, можно рассматривать как результат двух независимых движений — горизонтального равномерного и вертикального равноускоренного (свободного падения без начальной скорости или движения тела, брошенного вертикально вверх).

4. Движение материальной точки по кругу. Угловая скорость . Угловое ускорение .

Равномерное движение материальной точки по окружности — это движение, при котором материальная точка за равные промежутки времени проходит равные по длине дуги окружности.

Равномерное движение тела по окружности — это частный и наиболее простой случай криволинейного движения. Хотя при таком движении модуль скорости остается постоянным, это движение с ускорением, которое является следствием изменения направления вектора скорости.

В окружающем нас мире мы часто сталкиваемся с подобным движением — при любом вращении твердого тела вокруг некоторой закрепленной оси все точки этого тела движутся по окружностям.

Углова́я ско́рость — величина, характеризующая скорость вращения материальной точки вокруг центра вращения. 

ω = ϕ/t Угол ϕ T время

Угловое ускорение - псевдовекторная физическая величина, равная первой производной от псевдовектора угловой скорости по времени.

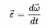Угловое ускорение характеризует интенсивность изменения модуля и направления угловой скорости при движении твердого тела.

5.Угловая скорость как вектор.

Угловая скорость является векторной величиной. Вектор угловой скорости ω может быть приложен к любой точке мгновенной оси и направлен в каждый момент времени по мгновенной оси Ω, так, чтобы, смотря навстречу этому вектору, видеть вращение тела происходящим против движения часовой стрелки.

6.Поступательное и вращательное движение твердого тела.

Поступательным называется такое движение абсолютно твердого тела, при котором любая прямая, жестко связанная с телом, перемещается параллельно самой себе. Все точки тела, движущегося поступательно, в каждый момент времени имеют одинаковые скорости и ускорения, а их траектории полностью совмещаются при параллельном переносе. Поэтому кинематическое рассмотрение поступательного движения абсолютно твердого тела сводится к изучению движения любой его точки. В самом общем случае поступательно движущееся твердое тело обладает тремя степенями свободы.

При вращательном движении все точки твердого тела движутся по окружностям, центры которых лежат на одной той же прямой, называемой осью вращения.Для описания вращательного движения нужно задать положение в пространстве оси вращения и угловую скорость тела в каждый момент времени.

Бесконечно малый поворот (dφ) — это поворот, который можно рассматривать как вектор.

7. Закон динамики поступательного движение твердого тела.

8.Центр масс твердого тела.

Центр масс геометрическая точка, характеризующая движение тела или системы частиц как целого^[1]. Не является тождественным понятию центра тяжести (хотя чаще всего совпадает).

9.Закон движения центра масс твердого тела .

Центр масс системы движется как материальная точка , в которой сосредоточена масса всей системы и на которую действует сила , равная геометрической сумме всех внешних сил , действующих на систему.

10.Моменты инерции материальной точки и твердого тела.

Моме́нт ине́рции — скалярная (в общем случае — тензорная) физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Момент инерции материальной точки относительно некоторой оси равен произведению ее массы на квадрат расстояния от точки до этой оси. J=m умножить на R квадрат. Момент инерции тела есть сумма моментов инерции материальных точек, составляющих это тело. J=Jц. т. +m умножить на S квадрат ц. т. - центр тяжести

11.Момент импульса материальной точки и твердого тела .

Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение^[1].

12.Моменты инерции простейших тел : кольца , цилиндра , стержня.

Цилиндр I=m*r^2

Стержень длины L и массы m I=(m*L^2)/3

Тонкое кольцо радиуса r и массы m I=(m*r^2)/2

13.Теорема Штейнера

Теорема Штейнера: момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_Cотносительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями:

где:

J_C — известный момент инерции относительно оси, проходящей через центр масс тела;

J — искомый момент инерции относительно параллельной оси;

m — масса тела;

d — расстояние между указанными осями.

14.Закон динамики вращения твердого тела.

Основной закон динамики вращательного движения твердого тела формулируется так: “Момент силы, действующий на вращающееся тело, равен произведению момента инерции тела на угловое ускорение”.

15.Закон сохранения момента импульса.

Закон сохранения момента импульса (закон сохранения углового момента): векторная сумма всех моментов импульса относительно любой неподвижной точки (или сумма моментов относительно любой неподвижной оси) для замкнутой системы остается постоянной со временем.

16.Работа при поворачивании тела на некоторый угол. Кинетическая энергия вращающегося твердого тела.

17.Гармонические колебания . Условия их возникновения .

Гармонические колебания — колебания, при которых физическая величина изменяется с течением времени по гармоническому (синусоидальному, косинусоидальному) закону.

Первое: наличие периодически изменяющейся силы, всегда направленной к положению равновесия. Второе: стремящаяся к нулю сила сопротивления окружающей среды.

18.Характеристики гармонических колебаний . Амплитуда , частота , фаза колебаний.

Амплиту́да максимальное значение смещения или изменения переменной величины от среднего значения при колебательном или волновом движении. 

Частота́ — физическая величина, характеристика периодического процесса, равна количеству повторений или возникновения событий (процессов) в единицу времени. V=n/t

Фаза колебаний – это аргумент периодической функции, описывающей колебательный процесс.

Представление гармонического колебания как проекции вектора , вращающегося с постоянной угловой скоростью.

19.Основное уравнение динамики гармонических колебаний .

20. Физический маятник .

Физи́ческий ма́ятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела

21.Скорость и ускорение при гармонических колебаниях.

22.Энергия гармонических колебаний.

Полная энергия гармонических колебаний равна сумме кинетической энергии и потенциальной энергии:

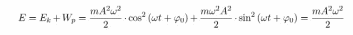
23.Сложение гармонических колебаний одной частоты и направление.

24.Сложение взаимно-перпендикулярных гармонических колебаний одной частоты .

25.Затухающие колебания . Уравнение осциллятора с затуханием. Частота затухающих колебаний.

Затухающие колебания — колебания, энергия которых уменьшается с течением времени. 

26.Амплитуда затухающих колебаний . Время затухания и логарифмический декремент затухания.

Множитель  , стоящий перед периодической функцией  , называется амплитудой затухающих колебаний. Она экспоненциально убывает со временем. Скорость затухания определяется величиной  . Время, по истечении которого амплитуда колебаний уменьшается в   раз, называется временем затухания  . За это время система совершает   колебаний. Затухание колебаний принято характеризовать логарифмическим декрементом затухания. Логарифмическим декрементом затухания называется логарифм отношения амплитуд в моменты последовательных прохождений колеблющейся величины через максимум или минимум:

.

Он связан с числом колебаний   соотношением:

.

27.Вынужденные колебания. Резонанс.

Вынужденные колебания — колебания, происходящие под воздействием внешних периодических сил.

Резона́нс (фр. resonance, от лат. resono «откликаюсь») — частотно-избирательный отклик колебательной системы на периодическое внешнее воздействие, который проявляется в резком увеличении амплитуды стационарных колебаний при совпадении частоты внешнего воздействия с определёнными значениями, характерными для данной системы

\

28.Основные положения МКТ и ее опытное обоснование . Броуновское движение.

Молекулярно-кинетическая теория (сокращённо МКТ) — теория XIX века, рассматривавшая строение вещества, в основном газов, с точки зрения трёх основных приближенно верных положений: - все тела состоят из частиц, размером которых можно пренебречь: атомов, молекул и ионов; - частицы находятся в непрерывном хаотическом движении (тепловом) ; - частицы взаимодействуют друг с другом путём абсолютно упругих столкновений. Основными доказательствами этих положений считались: - Диффузия - Броуновское движение - Изменение агрегатных состояний вещества

Бро́уновское движе́ние — беспорядочное движение микроскопических видимых взвешенных в жидкости или газе частиц твёрдого вещества, вызываемое тепловым движением частиц жидкости или газа.