Конкретная математика. Лекция 2. Вычисление конечных сумм, часть 1. Обозначения сумм.

Для сумм обычно используется сигма-обозначение с помощью значка ∑. Существует 2 основных обозначения – с явными пределами и с неявными пределами.

Пример обозначений с явными пределами: .

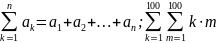При обозначениях с неявными пределами записываются условия на один или более индексов, которые означают, что производится суммирование по всем целым значениям индексов, удовлетворяющим всем этим условиям: .

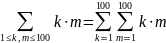В общем виде сигма-обозначения сумм запишем как .

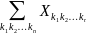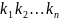- называются индексами суммирования, 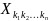– общим членом суммы.

Существует связь между суммами и рекуррентностями. Запись 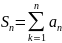эквивалентна рекуррентности:

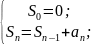
Законы преобразования сумм.

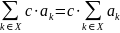распределительный закон

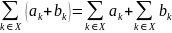сочетательный закон

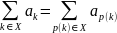переместительный закон

Распределительный закон разрешает вводить и выводить постоянные под знак и за знак ∑. Сочетательный закон позволяет разбивать одну сумму на две или объединять две суммы в одну. Переместительный закон гласит, что члены суммы можно переставлять в любом требуемом порядке; здесь р(к)—некоторая перестановка множества всех целых чисел.

Репертуарный метод вычисления рекуррентных соотношений и суммы.

Сначала мы подбираем величины общих параметров, для которых мы знаем решение,— это обеспечивает нас репертуаром разрешимых частных решений. Затем, комбинируя частные решения, мы получаем общее решение. При этом необходимо столько независимых частных решений, сколько имеется независимых параметров. На прошлой лекции мы решили рекуррентное соотношение из задачи Иосифа Флавия .

Этим методом можно решить более общую задачу

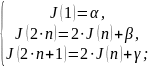
Запишем 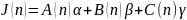. Далее можно найти:

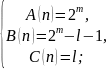
Другой пример для случая : 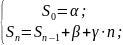Решение:

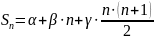
Эта формулу можно применить, например, для вычисления суммы 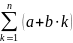. Записывая эту сумму в виде рекуррентного соотношения с параметрами 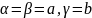, получаем:

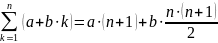
Метод суммирующего множителя.

Нетрудно заметить, что далеко не все рекуррентные соотношения можно сразу непосредственно привести к сумме. Например, из задачи про ханойскую башню:

Чтобы это было возможно, здесь можно использовать метод суммирующего множителя. Для этого домножаем в равенствах правые и левые части на 2^-n. Тогда, обозначив S_n = T_n*2^-n :

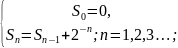
Пример: 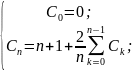Чтобы решить эту рекуррентность, вначале домножим на n, потом запишем точно такое же равенство для (n-1) и вычтем его из равенства для n. В итоге получим:

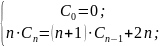
Любую рекуррентность вида 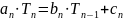можно упростить с помощью суммирующего множителя 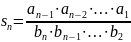. В этой задаче это 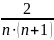. Тогда

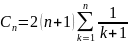
Обобщение задачи разрезания плоскости на n-мерное пространство.

Вначале рассмотрим задачу разрезания пространства n плоскостями в пространстве. Обозначим за S_n максимальное количество пространственных областей, на которые n плоскостей разбивают трёхмерное пространство. Как и на прошлой лекции, обозначим за L_n количество соответствующих двумерных областей на плоскости, на которые её разбивают n прямых. Новая n-я плоскость (при n > 0) увеличивает число пространственных областей на то количество замкнутых плоских областей, на которые прямые пересечения этой плоскости с другими плоскостями делят её. Две плоскости могут пересекаться не более чем по одной прямой. Поэтому новая плоскость может пересекать n — 1 старых плоскостей не более чем по n—1 различных прямых, а значит S_n<= S_n-1+L_n-1. Более того, легко показать по индукции, что в этой формуле можно достичь равенства. Мы проводим n-ю плоскость так, чтобы она не была параллельна никакой другой (следовательно, она пересекает каждую из них) и так, чтобы она не проходила ни через одну из имеющихся прямых пересечения, (следовательно, она пересекает каждую из плоскостей по различным непараллельным друг другу прямым). Поэтому рекуррентное соотношение имеет вид:

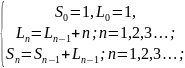
Для 4-мерного пространства будет

:

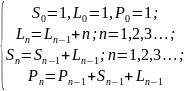Аналогично для большей размерности. Существует тем не менее довольно простая общая формула, которую несложно доказать по индукции, а прямой естественный её вывод будет приведён в этих лекциях позже:

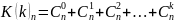
Здесь k – размерность пространства, которое разрезают (k-1)-мерными гиперплоскостями.