Конкретная математика. Лекция 1. Возвратные задачи. Задача о ханойской башне.

Задача состоит в том, чтобы переместить всю башню их 8 дисков на один из других колышков, перенося каждый раз только один диск и не помещая больший диск на меньший.

Наилучший способ разрешить вопрос, подобный нашему,— несколько обобщить его. Посмотрим, что будет в случае n дисков. Одно из преимуществ такого рода обобщения состоит в том, что можно будет даже еще уменьшить размер задачи. Полезно вначале рассмотреть крайние случаи. Совершенно ясно, как перемещать башню, состоящую только из одного или двух дисков, а после нескольких попыток становится понятно, как перемещать башню из трех дисков. Следующий шаг в решении задачи —выбор подходящего обозначения: обозначай и властвуй. Будем говорить, что Т_n есть минимальное число перекладываний, необходимых для перемещения n дисков с одного колышка на другой по правилам . Тогда T₁, очевидно, равно 1, а Т₂ равно 3. Можно получить дополнительную информацию, причем совершенно бесплатно, если рассмотреть самый крайний случай: ясно, что Т₀ = 0, поскольку для перемещения башни из n=0 дисков вообще не требуется ни одного перекладывания! Но давайте теперь изменим точку зрения и попробуем подумать о главном — как переместить высокую башню? Эксперименты с тремя дисками показывают, что решающая идея состоит в переносе двух верхних дисков на средний колышек; затем переносится третий диск и на него помещаются два других. Это дает ключ к общему правилу перемещения n дисков: сначала мы перемещаем n— 1 меньших дисков на любой из колышков (что требует T_n-1 перекладываний), затем перекладываем самый большой диск (одно перекладывание) и, наконец, помещаем n— 1 меньших дисков обратно на самый большой диск (еще T_n-1 перекладыва-

ний). Таким образом, n дисков (при n > 0) можно переместить самое большее за 2T_n-1 + 1 перекладываний: T_n <= 2T_n-1 + 1. Нет ли более короткого пути? Оказывается, что нет. На некотором этапе мы обязаны переместить самый большой диск. Когда мы это делаем, n — 1 меньших дисков должны находиться на одном колышке, а для того чтобы собрать их вместе, потребуется по меньшей мере T_n-1 перекладываний. Самый большой диск можно перекладывать и более одного раза, если мы не очень расторопны. Но после перемещения самого большого диска в последний раз мы обязаны поместить n — 1 меньших дисков (которые опять должны находиться на одном колышке) обратно на наибольший диск, что также требует T_n-1 перекладываний. Следовательно¸ T_n >=2T_n-1 + 1. Это значит, что T_n =2T_n-1 + 1. 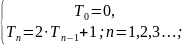(1.1) - совокупность подобных равенств называется рекуррентным соотношением. Найдём прямую формулу. T₀ = 0, T₁ = 1, T₂ = 3, T₃ = 7, T₄ = 15, T₅= 31, T₆ = 63. Очень похоже на 2ⁿ-1. Для произвольного номера n это можно доказать с помощью метода математической индукции.

Математическая индукция — это общий способ доказательства, что некоторое утверждение о целом числе n справедливо при любом n >= n₀. Сначала данное утверждение доказывается, когда n принимает свое наименьшее значение, n₀; это называется базой или основанием. Затем данное утверждение доказывается для n > n₀, в предположении, что оно уже доказано для всех п между n₀ и n — 1 включительно; это называется индукцией или индуктивным переходом. Такого рода доказательство позволяет получить бесконечное число результатов при конечном объеме работы. В нашем случае база индукции тривиальна, поскольку Т₀ = 2⁰ —1 = 0, а индуктивный переход выполняется для n > 0, когда n заменяется на n — 1: T_n = 2T_n-1 + 1 = 2(2^n-1-1)+ 1 = 2ⁿ-1. Следовательно, общая формула доказана для любого n =1,2,3….