ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
«Московский технический университет связи и информатики»
(МТУСИ)
Контрольная работа по теме:
«Функциональные устройства аппаратных средств вычислительной техники»
Практикум по дисциплине:
«Аппаратные средства вычислительной техники»
Вариант № 4
Дисциплина:
«Вычислительная техника»
Выполнила студентка: Баку Светлана Михайловна _________________ |
Группа: 2БВМ1501 |
Руководитель: Жуков Г.В. |
Москва 2017 г.
Содержание
Введение 3
Краткие теоретические сведения 3
Решение контрольной работы по варианту задания №4 6
Минимизация функции по нулевым и единичным наборам. 6
Синтез логических схем устройства в базисы «ИЛИ-НЕ», «И-НЕ», «И-ИЛИ-НЕ» 7
Логические схемы 9
Таблицы истинности логических схем 11
Временные диаграммы работы логических схем 14
Введение
Цель работы: изучение методов разработки комбинационных устройств (конечных автоматов без памяти) АСВТ.
Краткие теоретические сведения
Функция F(A1, A2, …, An) называется логической, если она, так же как и её аргументы, может принимать только два значения: 0 и 1. Совокупность значений аргументов, определяющих данное значение функции, называется набором . С наборами можно производить логические операции:
Конъюнкция (логическое умножение) Х1*Х2 или Х1&Х2:
Х1 0 0 1 1
Х2 0 1 0 1
F 0 0 0 1
Дизъюнкция (логическая сумма) Х1 ˅ X2 или Х1+Х2:
Х1 0 0 1 1
Х2 0 1 0 1
F 0 1 1 0
Сложение по модулю «2» Х1⊕Х2:
Х1 0 0 1 1
Х2 0 1 0 1
F 0 1 1 0
Стрелка Пирса (логическое «ИЛИ – НЕ») Х1↑Х2:
Х1 0 0 1 1
Х2 0 1 0 1
F 1 0 0 0
Штрих Шеффера (логическое «И – НЕ»), отрицание конъюнкции X1|X2 или
:
Х1 0 0 1 1
Х2 0 1 0 1
F 1 1 1 0
Логические функции могут быть представлены в виде алгебраических выражений, в виде таблиц истинности и обозначены с помощью логических элементов:
Конъюнкция:
Х1 |
Х2 |
У |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
Y=X1*X2
X2
Дизъюнкция:
Х1 |
Х2 |
У |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
Y=X1+X2
X2
Сложение по модулю 2:
Х1 |
Х2 |
У |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
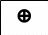Y=X1⊕X2
X2
Стрелка Пирса:
Х1 |
Х2 |
У |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
Y=X1↑X2
X2
Штрих Шеффера:
Х1 |
Х2 |
У |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
Y=X1|X2
X2
С помощью логических функций и логических элементов может быть разработана логическая схема любого функционального блока (или устройства) АСВТ.
При синтезе комбинационных устройств АСВТ используются канонические формы представления логических функций: совершенная дизъюнктивная нормальная форма (СДНФ) и совершенная конъюнктивная нормальная форма (СКНФ).
По этим формам может быть построена структурная схема логического устройства, но такая схема чаще всего получается сложной, с большим числом логических элементов, с низкой экономичностью и надежностью.
Для её упрощения применяются различные методы минимизации функций.