
- •Практичне заняття №3 (2 години)
- •Інструкція до виконання практичної роботи
- •Контрольні питання
- •Практичне заняття №4 (4 години)
- •2. Никитин е.М. Теоретическая механика для техникумов. – 12-е изд., испр. – м.: Наука. Гл. Ред. Физ.-мат. Лит., 1988. – 336 с. (с. 277-291)
- •Інструкція до виконання практичної роботи
- •1. Повторити основні теоретичні відомості з даної теми.
- •Розв’язок
- •3. Самостійно виконати запропоновані задачі за варіантами.
- •Контрольні питання
Практичне заняття №3 (2 години)
Тема: Обчислення основних кінематичних величин: траєкторії, відстані, шляху, прискорення.
Мета: навчитись застосовувати основні закони та формули до розв’язування типових задач з кінематики, закріпити вивчений теоретичний матеріал.
Тип заняття: формування практичних вмінь і навичок.
Вид заняття: практичне.
Література та ресурси мережі Інтернет:
1. Савельев И.В. Курс физики: Учеб.: В 3-х т. Т.1: Механика. Молекулярная физика. – М.: Наука. Гл. ред. физ.-мат. лит., 1989. – 352 с. (с. 97-99)
2. Никитин Е.М. Теоретическая механика для техникумов. – 12-е изд., испр. – М.: Наука. Гл. ред. физ.-мат. лит., 1988. – 336 с. (с. 233-249)
3. http://termeh-sorokin.on.ufanet.ru
4. http://gendocs.ru
Інструкція до виконання практичної роботи
1. Повторити основні теоретичні відомості з даної теми.
2. Розібрати типові задачі з даної теми.
Задача №1. Тіло обертається навколо нерухомої осі за законом φ = А + Вt + Ct2, де А = 5 рад, В = 8 рад/с, С = -1 рад/с2. Визначити повне прискорення точки, яка знаходиться на відстані R = 5 см від осі обертання, в момент часу t = 2 с.
Дано: |
Розв’язок |
φ = А + Вt + Ct2 А = 5 рад В = 8 рад/с С = -1 рад/с2 R = 5 см t = 2 с |
|
a – ? |
|
Відповідь: a ≈ 0,8 м/с2. |

Задача №2. На циліндр, який може вільно обертатись навколо горизонтальної осі, намотана нитка. До її кінця прив’язали тягарець та дали йому можливість опускатися. Рухаючись рівноприскорено, тягарець за 3 с опустився на 1,5 м. Визначити кутове прискорення циліндра, якщо його радіус 4 см.
Дано: |
Розв’язок |
t = 3 c υ0 = 0 h = 1,5 м R = 0,04 м
|
Для
рівноприскореного руху маємо:
Оскільки
Тому
Як
відомо,
Самостійне завдання: перевірте розмірність знайденої величини! |
ε – ?
|
|
Відповідь:
ε
≈ |
3. Самостійно виконати запропоновані задачі за варіантами.
Методичні вказівки до самостійного розв’язування задач. При розв’язуванні задач необхідно знати: поняття обертального руху тіла та його види; визначення лінійної швидкості тіла та її зв’язок з кутовою; поняття кутового прискорення тіла та формули для його обчислення; визначення тангенціального та нормального прискорення, формули для їх розрахунку та зв’язок з повним прискоренням тіла.
Розв’язок кожної задачі необхідно розпочинати з рисунку. Для перевірки вірності отриманого числового значення фізичної величини бажано виконати перевірку її розмірності.
Задача
1. Диск
обертається навколо нерухомої осі за
законом:
 (φ
– у радіанах, t
– у
секундах).
Знайти кутову швидкість та кутове
прискорення диску у моменти часу t1,
t2,
t3.
Описати
характер руху диску у кожний з моментів
часу.
(φ
– у радіанах, t
– у
секундах).
Знайти кутову швидкість та кутове
прискорення диску у моменти часу t1,
t2,
t3.
Описати
характер руху диску у кожний з моментів
часу.
№ ва-ріанту |
Вхідні дані |
№ ва-ріанту |
Вхідні дані |
В1 |
|
В6 |
|
В2 |
|
В7 |
|
В3 |
|
В8 |
|
В4 |
|
В9 |
|
В5 |
|
В10 |
|
Задача 2. Колесо обертається навколо нерухомої осі так, що кут його повороту залежить від часу як φ = Ct2. У момент часу t0 лінійна швидкість точки на ободі колеса υ0. Визначити повне прискорення α цієї точки.
№ ва-ріанту |
Вхідні дані |
№ ва-ріанту |
Вхідні дані |
В1 |
C=0,7 рад/с2; t0 = 1,5 с; υ0 = 0,5 м/с |
В6 |
C=1 рад/с2; t0 = 1 с; υ0 = 4 м/с |
В2 |
C=0,5 рад/с2; t0 = 1 с; υ0 = 0,2 м/с |
В7 |
C=1 рад/с2; t0 = 2 с; υ0 = 8 м/с |
В3 |
C=0,2 рад/с2; t0 = 2 с; υ0 = 0,4 м/с |
В8 |
C=0,5 рад/с2; t0 = 2 с; υ0 = 4 м/с |
В4 |
C= -0,5 рад/с2; t0 = 1 с; υ0 = -0,5 м/с |
В9 |
C= -1 рад/с2; t0 = 3 с; υ0 = -6 м/с |
В5 |
C= -0,2 рад/с2; t0 = 2 с; υ0 = -1 м/с |
В10 |
C= 0,1 рад/с2; t0 = 5 с; υ0 = 0,5 м/с |
Задача 3. Маховик має у деякий момент часу кутову швидкість ω та кутове прискорення ε. Знайти швидкість, тангенціальне, нормальне, повне прискорення точки маховика, що знаходиться на відстані r від осі обертання. На рисунку зобразити вектори всіх знайдених величин.
№ ва-ріанту |
Вхідні дані |
№ ва-ріанту |
Вхідні дані |
В1 |
ω=π рад/с; ε= -1 рад/с2; r=0,4 м |
В6 |
ω= 2π рад/с; ε=4 рад/с2; r=0,6 м |
В2 |
ω=2π рад/с; ε= -3 рад/с2; r=0,8 м |
В7 |
ω= 1,5π рад/с; ε=2 рад/с2; r=0,8 м |
В3 |
ω= -2π рад/с; ε= 3 рад/с2; r=0,4 м |
В8 |
ω= -π рад/с; ε= -1 рад/с2; r=0,4 м |
В4 |
ω= -π рад/с; ε=2 рад/с2; r=0,5 м |
В9 |
ω= -2π рад/с; ε= -2 рад/с2; r=0,5 м |
В5 |
ω= 3π рад/с; ε=1 рад/с2; r=0,6 м |
В10 |
ω= 1,2π рад/с; ε= 1 рад/с2; r=0,6 м |


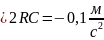
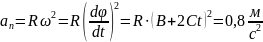
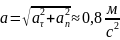
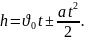
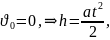
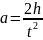
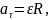

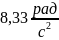 .
. ;
t1=0;
t2=6
с;
t3=7
с
;
t1=0;
t2=6
с;
t3=7
с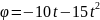 ;
t1=0;
t2=2
с; t3=4
с
;
t1=0;
t2=2
с; t3=4
с ;
t1=0;
t2=2
с; t3=5
с
;
t1=0;
t2=2
с; t3=5
с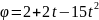 ;
t1=0;
t2=2
с; t3=5
с
;
t1=0;
t2=2
с; t3=5
с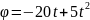 ;
t1=0;
t2=2
с; t3=4
с
;
t1=0;
t2=2
с; t3=4
с ;
t1=0;
t2=2с;
t3=3
с
;
t1=0;
t2=2с;
t3=3
с ;
t1=0;
t2=5
с; t3=10
с
;
t1=0;
t2=5
с; t3=10
с ;
t1=0;
t2=4
с; t3=8
с
;
t1=0;
t2=4
с; t3=8
с ;
t1=0;
t2=5
с; t3=7
с
;
t1=0;
t2=5
с; t3=7
с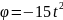 ;
t1=0;
t2=5
с;
t3=10
с
;
t1=0;
t2=5
с;
t3=10
с