20% Раствор. Если вместо чистой воды добавить 5 литров 80% раствора, то
получился бы 70%) раствор поваренной соли. Сколько было 40% и 60%
растворов?
Составляем систему 2 уравнений:
40х + 60у + 5 * 0 = 20 ( х + у + 5 )
40х + 60у + 400 = 70 ( х + у + 5 )
Ответ: х = 1; у = 2.
ЕГЭ 2003г. Уровень - В
В
двух сосудах содержится раствор кислоты
в первом -70%, во втором - 46%. Из первого
сосуда 1 л раствора перелили во второй
и жидкость перемешали, затем из 2 сосуда
1л раствора перелили в 1 и также перемешали,
после чего концентрация
в 1 сосуде стала 68%.Сколько жидкости
было во 2 сосуде, если в1
сосуде ее было 10л.
Аналогично решается система уравнений
Ответ: х = 5, у = 50
ЕГЭ 2003г. Уровень - В
Имеются 2слитка, представляющие собой сплавы цинка и меди. Масса 1 слитка 2 кг, 2-Зкг. Эти два слитка сплавили вместе с 5 кг сплава цинка и меди, в котором цинка было 45% и получили сплав, в котором цинка стало 50%, если бы процентное содержание цинка в 1 слитке было бы такое же как во 2, а во втором такое же как в 1, то сплавив эти 2 слитка с 5 кг сплава цинка с медью в котором 60% цинка получили бы сплав, в котором содержится 55% цинка. Найдите процентное содержание цинка в 1 и 2 слитках.
С
оставляем
систему уравнений:
2х + Зу + 225 = 500
2у + 3х + 300 = 550
Ответ: 40%, 65%.
ЕГЭ-2005 г. Уровень С
Н
а
овощной базе имелся крыжовник. Влажность,
которого составляла 99%.3а время
хранения его влажность уменьшилась на
1%. На сколько процентов уменьшилась
масса хранившегося крыжовника?
Составляем уравнение:
99 х – 100 у = 98 ( х - у)
х = 2 у
(х - у) / х = (2у-у) / 2
у = у / 2
у =1 / 2
Ответ: масса уменьшилась вдвое, значит на 50%.
ЕГЭ-2005 г. В -7
И
меются
2 слитка сплава серебра и олова. Первый
слиток содержит 380г серебра и 40 г олова,
а второй слиток 450 г серебра и 150 г олова.
От каждого слитка взяли по куску,
сплавили их и получили 200 г сплава, в
котором оказался 81 % серебра. Определите
массу в граммах куска , взятого от
второго слитка.
Составляем систему уравнений:
а + b = 200
а х + b х = 81 * 200
36 000 = 400 х
45 000 = 600 у
Ответ: 120 г.
ЕГЭ-2005 г. Уровень С
В
свежих яблоках 80% воды, а в сушеных 20 %.
На сколько % уменьшилась масса
яблок при сушке?
80 х – 100 у = 20 х – 20 у
60 х = 80 у
х = 80 у / 60 = 4 у / 3
Ответ:75%
ЕГЭ-2005 г. Уровень С
На 1 поле 65 % площади засеяно овсом, на 2 поле под овсом занято 45%площади. Известно, что на 1 и 2 полях вместе под овсом занято 53% общей площади. Какую часть всей площади составляет 1 поле?
Ответ: 40%.
ЕГЭ-2005 г. Уровень С
И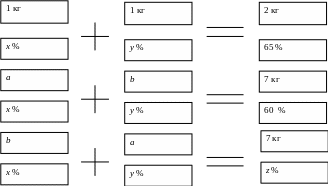
меется
два разных сплава меди со свинцом. Если
взять 1 кг 1 сплава и 1 кг 2сплава
и перемешать их, то получится сплав с
содержанием 65% меди . Известно,
что если взять кусок номер 1 первого
сплава и кусок номер 2второго
сплава, имеющих суммарную массу 7 кг и
перемешать их, то получится сплав с
содержанием меди 60%. Какова масса меди
,содержащаяся в сплаве, если переплавить
кусок 1 сплава равного по массе 2куска
и 2 сплава равного по массе куску 1
сплава.
Составляем систему уравнений:
х + у = 130
а х + b у = 420
b х + а у = 7 z
а + b = 7
1) х + у = 130
b x + b y = 130 b
b x = 130 b – b y
2) x + y = 130
a x + a y = 130 a
a y = 130 a – a x
b x + a y = 130 b – b y + 130 a – a x = 130 ( b+ a ) – ( a x + b y ) = 130 * 7 – 420 = 490
7 * z = 490
z = 70
7* 0, 7 = 4,9 кг
Ответ: 4,9 кг.