4. Определение расстояния между скрещивающимися прямыми.

Кратчайшее расстояние между скрещивающимися прямыми определяется величиной перпендикуляра, заключенного между параллельными плоскостями, которым принадлежат скрещивающиеся прямые. Эти плоскости называют плоскостями параллелизма.

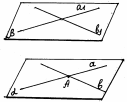
Для того чтобы через скрещивающиеся прямые k и b провести взаимно параллельные плоскости α и β, достаточно через точку A (A ∈ k) провести прямую m, параллельную прямой b, а через точку B (B ∈ b) прямую n, параллельную прямой k.

Пересекающиеся прямые k и m, b и n определяют взаимно параллельные плоскости α и β. Расстояние между плоскостями α и β равно искомому расстоянию между скрещивающимися прямыми k и b.

В качестве примера решаем задачу на кратчайшее расстояние между скрещивающимися прямыми способом перемены плоскостей проекций. Здесь они заданны отрезками [AB] и [CD].

Кратчайшее расстояние между скрещивающимися прямыми способом прямоугольного треугольника

[KA] - кратчайшее расстояние между скрещивающимися прямыми q и p.

7. Параллельность прямой и плоскости. Параллельность плоскостей.

Согласно аксиомам, если две точки прямой находятся в некоторой плоскости, то прямая лежит в этой плоскости. Отсюда следует, что возможны три случая взаимного расположения прямой и плоскости в пространстве:

1) прямая лежит (находится) в плоскости

2) прямая и плоскость имеют только одну общую точку (прямая и плоскость пересекаются)

3) прямая и плоскость не имеют общих точек

Прямая и плоскость называются параллельными, если они не имеют общих точек.

Теорема 5 „Признак параллельности прямой и плоскости”. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой на этой плоскости, то эта прямая параллельна данной плоскости. 

Теорема 6. Если плоскость β проходит через данную прямую a, параллельную плоскости α, и пересекает эту плоскость по прямой b, то b∥a.

 

Прямую b иногда называют следом плоскости β на плоскости α.

Теорема 7. Если одна из двух параллельных прямых a∥b параллельна данной плоскости α, то другая прямая либо параллельна этой плоскости либо лежит в этой плоскости.

Определение. Две плоскости называются параллельными, если они не имеют общих точек. Параллельность плоскостей   и   обозначается так:   ||  . Рассмотрим признак параллельности двух плоскостей. Теорема. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

Случаи взаимного расположения плоскостей:

плоскости   и   пересекаются
	плоскости   и   параллельны.

Свойства параллельных плоскостей:

	1. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
	2. Отрезки параллельных прямых, заключённые между параллельными плоскостями, равны.