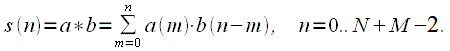1. Обобщенная схема цифровой обработки сигналов

2. Типовые дискретные сигналы

3. Дискретные экспоненциальные функции

4. Дискретное преобразование Фурье и его свойства

5. Циклическая и линейная свертка

6. Преобразование Хаара

7. Корреляция, вычисление прямым методом и с помощью дискретных преобразований

8. Алгоритм БПФ с прореживанием по времени

9. Передаточная функция ЦФ

10. Алгоритм БПФ с прореживанием по частоте

11. Преобразование Уолша-Адамара и его свойства

12. Низкочастотная фильтрация изображений в пространственной области

13. Глобальные методы улучшения контраста полутоновых изображений

14. Линейные методы контрастирования изображений

15. Принципы и особенности пространственной фильтрации изображений

16. Улучшение качества бинарных изображений

17. Вычисление сверток при помощи дискретных преобразований

18. Обработка бинарных изображений на основе математической морфологии

19. Связность в изображениях

20. Глобальная бинаризация полутоновых изображений

21. Обработка полутоновых изображений на основе математической морфологии

22. Быстрое преобразование Уолша-Адамара

23. Классификация методов распознавания объектов изображений

24. Структурные методы распознавания объектов изображений

25. Фильтрация изображений в частотной области

26. Базовая структура анализатора спектра на основе ДПФ

27. Цифровые фильтры, их математическое описание, особенности некурсивных и нерекурсивных

28. Основные шаги стандарта сжатия JPEG

29. Параметры анализаторов спектра

30. Нелинейные методы контрастирования изображений

1. Обобщенная схема цифровой обработки сигналов цепочка функциональных преобразований сигнала вида [11]: / / / / / А А Ц Ц Ц Ц А А А ⇒⇒⇒⇒ («аналог/аналог», «аналог/цифра», «цифра/цифра», «цифра/аналог», «аналог/аналог»реализуемых соответственно аналоговым фильтром нижних частот ФНЧ1, аналого-цифровым преобразователем АЦП, процессором ЦОС, цифроаналоговым преобразователем ЦАП и аналоговым фильтром нижних частот ФНЧ2.

2. Типовые дискретные сигналы

При исследовании линейных дискретных систем ряд дискретных сигналов используют в качестве испытательных воздействий; такие сигналы называют типовыми. К ним относятся: Цифровой единичный импульс

Задержанный цифровой единичный импульс

Цифровой единичный скачок

Задержанный цифровой единичный скачок

Дискретная экспонента,

Дискретный гармонический сигнал

где T – период дискретизации; A – амплитуда; ω – круговая частота, связанная с частотой ƒ коэффициентом пропорциональности 2π Дискретная косинусоида

в результате замены непрерывного времени дискретным (рис. 1.9)

s(nT) = s(n) = Acos(ωt) |t=nT = Acos(ωTn).

Дискретный комплексный гармонический сигнал

3.Дискретные экспоненциальные функции

В дискретном преобразовании Фурье используется система дискретных экс-

поненциальных функций (ДЭФ), которая определяется следующим выражением:

где j = − 1 ; k и n принимают целочисленные значения (0,1,2,...,N − 1) . Перменную k отождествляют с номером функции, а переменную n — с номером отсчета.

4. Дискретное преобразование Фурье и его свойства

прямое преобразование,

Обратноепреобразование

где {f (k)}- дискретный спектр

Спектр — это представление зависимости частот периодического сигнала.

Процесс фиксации параметров исходного аналогового сигнала через определенные равные интервалы времени называется дискретизацией

Свойства ДПФ

1. Периодичность.

f ( Nl ± k ) = f ( ±k ); s( Nl ± n ) = s( ±n ).

2. Связь с коэффициентами ряда Фурье

Если частота дискретизации выбрана в соответствии с теоремой Котельникова, то при дискретизации периодической аналоговой функций s( t ) ДПФ позволяет по выборкам s( n ) найти спектр f ( k ) ,который на интервале 0 ≤ k ≤ N − 1равен спектру исходной функции s( t ).

3. Линейность.

4. Инвариантность относительно сдвига по времени и частоте.

5.Теорема о свертке.

Теорема о свертке утверждает, что спектр свертки равен произведению спектров сворачиваемых последовательностей,

6. Теорема о корреляции.

Спектр корреляционной функции последовательностей равен роизведению их спектров, причем один из спектров берётся в комплексном сопряжении,

7. ДПФ вещественных последовательностей.

8. Равенство Парсеваля

энергия сигнала равна суммарной энергии спектральных компонент, т.е. энергия сигнала больше никуда не расходуется

5. Циклическая и линейная свертка

Свертка – это математический способ комбинирования двух сигналов для формирования третьего сигнала

Линейной сверткой сигналов   и  называется дискретный сигнал вида:

(2)

Циклическая свертка определяется для периодических последовательностей длины N выражением

6. Преобразование Хаара

Преобразование Хаара можно рассматривать как процесс дискретизации исходного сигнала, при котором с переходом к сле­дующей строке вдвое уменьшается щаг дискретизации.

прямое преобразование

обратное

Для N=4

Для сигнала S=4 2,4,1,4

Обратное