Билет №5

Математические модели определения надежности системы следует разрабатывать с учетом возможной проверки и подтверждения надежности в соответствии с требованиями надежности.

В качестве оценки правильности выбора нормативного значения надежности рекомендуется использовать:

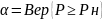
Математические модели надежности могут быть разбиты на две группы. Первая – это структурные модели. Они основаны на логических схемах взаимодействия элементов, входящих в систему, с точки зрения сохранения работоспособности системы в целом. При этом используют статическую информацию о надежности элементов без привлечения сведений о физических свойствах материала, деталей и соединений, о внешних нагрузках и воздействиях, о механизмах взаимодействия между элементами. Структурные модели представляют в виде блок-схем и графов (например, деревьев отказов, деревьев событий) (смотреть билет №14), а исходную информацию – в виде известных значений вероятности безотказной работы элементов, интенсивности отказов и т.п. Другая группа математических моделей теории надежности учитывает механические, физические и другие реальные процессы, которые ведут к изменению свойств объекта и его составляющих. Таковы модели механики, широко применяемые в расчетах машин и конструкций. Силовое и кинематическое взаимодействие элементов машин и конструкций носит сложный характер. Поведение этих объектов существенным образом зависит от их взаимодействия с окружающей средой, от характера и интенсивности процессов эксплуатации.

Для предсказания поведения деталей и элементов машин необходимо рассматривать процессы нагружения, деформирования, изнашивания, накопления повреждений и разрушения при переменных нагрузках,  температурных  и  других  внешних воздействиях. Оценить

показатели надежности систем можно расчетно-теоретическим путем, основанным на физических моделях и статических данных относительно свойств материалов, нагрузок и воздействий [1].

Математическая модель – совокупность математических объектов (чисел, символов, множеств и т.д.) и связей между ними, отражающих важнейшие свойства технической системы: логической, учитывающей возможные состояния системы, пути и интенсивности переходов из одного состояния в другое, или функциональной, содержащей границы допуска на определяющие параметры и зависимости этих параметров от случайных возмущений и процессов в элементах.

Математическое моделирование – процесс создания имитирующей математической модели и ее использования с целью получения сведений о реальном объекте.

Математическое моделирование является альтернативой физическому моделированию, но у него есть ряд существенных достоинств: меньшие сроки на подготовку, значительно меньшая материалоемкость, возможность выполнения экспериментов на предельных и запредельных режимах и другое.

Для моделирования необходимо определить исследуемую техническую систему.

Установить границы.

Основные переменные.

 Константы.

Показатели эффективности.

Подобрать подходящую модель.

Описать ее на математическом языке, доказать адекватность модели реальному объекту.

Спланировать и провести эксперимент.

Обработать результаты.