Пример решения задачи к3

Пример 1: Дано: , см, (см), с.

Определить: абсолютную скорость и абсолютное ускорение точки М.

Решение:

При решении задачи считаем движение точки по пластине относительным, а вращательное движение самой пластины – переносным. Выбираем подвижную и неподвижную системы координат (рис. 14.4).

Определим положение точки на пластинке в момент времени с:

см.

Знак «минус» показывает, что точка М перемещается в сторону, противоположную положительному направлению отсчёта расстояния АМ вниз вдоль оси относительно точки А.

Точка М совершает сложное движение. Относительное движение – это движение точки М по пластинке вдоль оси ₁, а переносным движением будет вращение системы координат , неизменно связанной с пластиной, относительно неподвижной системы координат .

Рис. К3 1

Абсолютная скорость .

Относительная скорость ; .

При с см/с, знак «минус» показывает, что вектор направлен вниз вдоль оси относительно точки А, в сторону отрицательных значений.

, =120 см/с.

Переносная скорость

,

где см, так как ОАМ – прямоугольный равнобедренный треугольник, так как см; см, и . Модуль угловой скорости , , при с с^-1, знак «минус» показывает, что пластинка вращается в сторону, противоположную положительному направлению отсчёта угла (рис. 14.4), по часовой стрелке, а вектор перпендикулярен плоскости XOY чертежа и направлен вдоль оси, проходящей через точку О, за чертеж.

с^-1, см/с.

Вектор и направлен в сторону в сторону вращения пластины.

Угол между и равен 45°, тогда

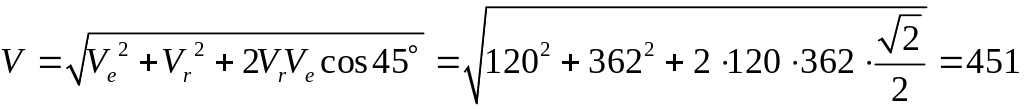см/с.

Абсолютное ускорение , или .

Относительное касательное ускорение

; .

При с см/с, см/с² и направлено противоположно так как = -120 см/с.

Относительное движение точки М направлено по прямой АВ, поэтому

Переносное касательное ускорение , где угловое ускорение , . При с с^-2. Знаки и совпадают, значит, вращение пластинки ускоренное, направления и совпадают.

с^-2, см/с².

Переносное нормальное ускорение см/с² и направлено от М к О.

Ускорение Кориолиса

см/с².

Вектор направлен в соответствии с векторным равенством параллельно оси ОХ (рис. 14.4).

Модуль абсолютного ускорения определим методом проекций:

см/с²;

см/с²;

см/с².

Пример 2: Диск радиусом R = 20 см вращается вокруг оси, перпендикулярной плоскости диска и проходящей через точку О, согласно уравнению . По ободу диска от точки А движется точка М согласно уравнению см. Для момента времени t = 1 с определить величину абсолютной скорости и абсолютного ускорения точки М (рис. К3.2).

Рис. К3.2

Решение:

Убедимся, что точка М совершает сложное движение. Действительно, точка М движется по ободу диска и вместе с диском вращается вокруг оси О.

Движение точки М по ободу диска по заданному закону будет относительным, вращение диска вокруг оси Опереносным.

Установим положение точки М на относительной траектории в данный момент времени, определив для этого значение центрального угла .

, т. е. .

Положение точки М в данный момент времени указано на рисунке.

Абсолютная скорость точки М определяется геометрической суммой относительной и переносной скоростей

.

Относительное движение точки является криволинейным. Поэтому вектор относительной скорости направлен по касательной к ободу диска в точке М. Значение относительной скорости

, при t = 1 с см/с.

Переносное движение, т. е. движение диска, является вращательным. Поэтому вектор переносной скорости, т. е. скорости той точки диска, с которой в данный момент совпала точка М, будет направлен перпендикулярно отрезку ОМ в сторону вращения диска. По модулю

, где .

При t = 1 с с^-1. Значение см.

Тогда см/с.

Модуль абсолютной скорости определяем по формуле

см/с.

Для определения абсолютного ускорения точки М используем формулу абсолютного ускорения точки в развернутом виде

.

Относительное нормальное ускорение равно:

см/с².

Вектор направлен по радиусу диска к его центру С.

Относительное касательное ускорение

см/с².

Вектор совпадает с направлением вектора относительной скорости. Переносное нормальное ускорение

см/с².

Вектор направлен вдоль ОМ к оси вращения О. Переносное касательное ускорение , где угловое ускорение , при t = = 1 с с^-2.

Тогда см/с².

Так как угловая скорость и угловое ускорение одинаковы по знаку, то вектор совпадает с направлением вектора переносной скорости.

Ускорение Кориолиса определим по формуле

.

Так как вектор относительной скорости лежит в плоскости, перпендикулярной оси переносного вращения, то для определения направления кориолисова ускорения достаточно вектор относительной скорости повернуть в сторону вращения на 90˚ в плоскости диска. По модулю кориолисово ускорение равно:

, или см/с².

Модуль абсолютного ускорения найдем методом проекций:

см/с²,

см/с².

Окончательно модуль абсолютного ускорения равен:

м/с².