5.2. Пример выполнения индивидуального задания

1. Для заданного автомата найдите: самую короткую цепочку, распознаваемую автоматом; три другие цепочки, распознаваемые этим автоматом; три цепочки, которые отвергаются автоматом.

	0	1
A	B	C	0
B	A	C	0
C	A	F	0
D	B	F	0
F	D	A	1

Р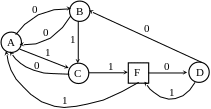 ешение. Построим для данного автомата граф переходов, что позволит определять нужные цепочки из входных символов. Состояния, находящиеся в квадрате, являются допускающими, остальные (в кружочках)– отвергающими.

а) Самая короткая цепочка, распознаваемая автоматом ;

б) три другие допустимые цепочки: 011, 0011, 00011;

Например: – допустимая;

– допустимая;

– допустимая;

в) три отвергающие: 01, 100, 11011.

Например: – отвергающая;

– отвергающая;

– отвергающая.

2. Опишите словами множество цепочек распознаваемых конечным автоматом:

	0	1
A	B	С	1
B	D	B	0
C	C	D	0
D	D	D	1

Решение. Построим для данного автомата граф переходов:

Автомат допускает цепочки трех типов:

• цепочки начинаются с 0, затем идет, возможно пустая, последовательность 1, потом следует 0, а далее любая возможно пустая последовательность из 0 и 1;

• цепочки начинаются с 1, затем идет, возможно пустая, последовательность 0, потом следует 1, а далее любая возможно пустая последовательность из 0 и 1;

• пустая цепочка.

3. Для конечного автомата найдите входную цепочку минимальной длины такую, что под ее действием:

а) каждое возможное состояние имеет место хотя бы раз;

б) каждый возможный переход происходит хотя бы раз.

	0	1
A	D	A	0
B	A	C	0
C	A	F	0
D	B	C	0
E	B	C	1
F	E	A	1

Решение. Построим для данного автомата граф переходов:

а) по графу видно, что минимальной цепочкой, в ходе прочтения которой все состояния будут иметь место хотя бы раз, будет:

;

или, например, такая:

;

б) из всех возможных прохождений по графу нам нужно взять то, которое пройдет по всем ребрам графа. Это, например, может быть цепочка:

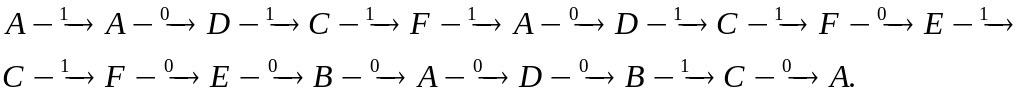
Итак, искомая цепочка: 101110110110000010.

4. Постройте конечный автомат с заданным входным алфавитом, который допускает в точности следующее множество цепочек:

Входную цепочку, содержащую подцепочку "FFAFA", если входной алфавит {F,A}.

Решение. Определим имена и назначение состояний.

А – начальное состояние – отвергающее состояние;

В – в цепочке есть F – 0 – отвергающее состояние;

С– в цепочке есть FF– 0 – отвергающее состояние;

D– в цепочке есть FFA – 0 – отвергающее состояние;

E– в цепочке есть FFAF – 0 – отвергающее состояние;

F– в цепочке есть FFAFA – 1 – допускающее состояние.

Автомат будет иметь следующую матрицу переходов:

	A	F
A	A	B	0
B	A	C	0
C	D	С	0
D	A	E	0
E	F	C	0
F	F	F	1

5. Постройте конечный автомат для множества цепочек из нулей и единиц, у которых за каждым вхождением пары 11 следует 0. Минимизируйте его. Затем превратите этот автомат в процессор с концевым маркером.

Решение. Определим смысл и имена состояний:

А – начальное состояние – 1 – допустимое состояние;

В – в цепочке есть 1 – 1 – допустимое состояние;

С – в цепочке есть 11 – 0 – недопустимое состояние;

D – в цепочке есть 110 – 1 – допустимое состояние;

E – состояние ошибки – 0 – недопустимое состояние;

Автомат будет иметь следующую таблицу переходов:

	0	1
A	A	B	1
B	A	C	1
C	D	E	0
D	A	B	1
E	E	E	0

Теперь минимизируем его.

1. Начнем с определения недостижимых состояний.

Помещаем во множество достижимых состояний начальное состояние V₀={A}.

И далее следуем указаниям алгоритма:

V₁={A, B}

V₂={A, B, C}

V₃={A, B, C, D, E}

Очевидно, что в автомате нет недостижимых состояний.

2. Теперь найдем эквивалентные состояния (алгоритм б):

Разбиваем все множество состояний на допустимые и недопустимые:

P₀=({A, B, D}, {C, E})

Затем по каждому входному символу разбиваем предыдущее разбиение, если состояния из одного подмножества имеют преемников в разных подмножествах:

0: P₁=({A, B, D}, {C}, {E});

1: P₂=({A, D}, {C}, {B}, {E});

0: P₃=({A, D}, {C}, {B}, {E});

Так как дальнейшее разбиение не происходит, то состояния A и D эквивалентны. Удаляем из автомата состояние D и заменяем его буквой A. Таблица переходов искомого процессора будет иметь вид:

	0	1	–|
A	A	B	да
B	A	C	да
C	A	нет	нет

6. Определить, эквивалентны ли два заданных автомата и, если возможно, найти для них различающую цепочку.

0

1

0

1

A

D

A

0

A

B

A

0

B

A

C

0

B

A

C

0

C

A

F

0

C

F

A

0

D

B

C

0

D

B

C

1

E

B

C

1

E

B

C

0

F

E

A

1

F

E

D

1

Решение. Два заданных автомата эквивалентны, если эквивалентны их начальные состояния. Меткой каждой строки таблицы эквивалентности является пара проверяемых начальных состояний (для первого и второго автомата). Справа (+/-) – обозначение допустимости/недопустимости состояний (если они оба допустимые или недопустимые, то ставим «+», иначе – «-»).

Далее по каждому входному символу мы записываем пары переходов для каждого автомата по этому символу. Новыми парами помечаем строки в левом столбце. Если исходная пара эквивалентна, то все полученные в ходе проверки пары тоже эквивалентны.

	0	1
(A, A)	(D, B)	(A, A)	+
(D, B)	(B, A)	(С, C)	+
(B, A)	(A, B)	(C, A)	+
(С, А)	(А, В)	(F, A)	+
(F, A)			–

Видно, что (F, A) – неэквивалентные состояния для двух автоматов, таким образом, исходная пара (А, А) также неэквивалентна. Из таблицы определим различающую цепочку 0011.

Для первого автомата: – допустимое состояние.

Для второго автомата: – отвергающее состояние.

7. Построить минимальный автомат эквивалентный данному.

	0	1	2
A	C	E	G	0
B	K	E	G	1
C	J	A	H	0
D	F	A	G	1
E	E	J	H	0
F	D	I	A	1
G	H	A	J	0
H	G	J	B	1
I	D	F	G	0
J	B	H	G	1
K	M	E	N	0
M	J	A	H	0
N	H	A	J	0

Решение. Исходя из определения минимального автомата, необходимо удалить недостижимые и объединить эквивалентные состояния данного автомата. Для определения множества недостижимых состояний вначале найдем множество достижимых состояний2.

1. V₀={A};

2. V₁={A, C, E, G};

3. V₂={A, C, E, G, J, H};

4. V₃={A, C, E, G, J, H, B};

5. V₄={A, C, E, G, J, H, B, K};

6. V₅={A, C, E, G, J, H, B, K, M, N};

7. V₆={A, C, E, G, J, H, B, K, M, N}.

Так как множества, построенные на шаге 6 и 7 совпадают, т. е. алгоритм перестал поставлять новые состояния, то недостижимыми являются те состояния, которые не попали в последнее множество: F, D, I.

Имеем следующую таблицу переходов для автомата без недостижимых состояний:

	0	1	2
A	C	E	G	0
B	K	E	G	1
C	J	A	H	0
E	E	J	H	0
G	H	A	J	0
H	G	J	B	1
J	B	H	G	1
K	M	E	N	0
M	J	A	H	0
N	H	A	J	0

Для нахождения эквивалентных состояний воспользуемся «методом разбиения», который заключается в разбиении множества состояний на непересекающиеся подмножества или блоки, такие, что неэквивалентные состояния попадают в разные блоки. Сначала все состояния разобьем на два блока: допускающих и отвергающих состояний.

Под действием входного символа 0 блок разбивается на блоки и , т. к. состояния , , переходят в состояния, принадлежащие первому блоку (а, именно, в состояния , , соответственно), тогда как состояния переходят в состояния, принадлежащие второму блоку (а, именно, в состояния , , , соответственно). Это означает, что для любого состояния из множества и любого состояния из соответствующие состояния-преемники по входу 0 будут неэквивалентны. Итак, новое разбиение имеет вид

.

Разбивая блок из относительно 0 получаем

.

Разбивая блок из относительно 0 получаем

.

Разбивая блок из относительно 0 получаем

.

не допускает дальнейшего разбиения. Чтобы убедиться в этом, заметим, что все состояния блока переходят относительно 0 в состояние блока , относительно 1 – в состояние блока , относительно 2 – в состояние блока . Аналогично, блок переходит в блоки , , относительно 0, 1, 2 соответственно. А блок переходит в блоки , , , относительно 0, 1, 2 соответственно. Оставшиеся блоки имеют по одному элементу и поэтому автоматически исключают дальнейшее разбиение.

Следовательно, состояния и , и , и являются эквивалентными. Объединим каждую пару состояний в одно новое, получим: , , . Подставляя эти новые имена в автомат и удаляя лишние строки, получим минимальный автомат, эквивалентный исходному:

	0	1	2
X	Y	E	Z	0
B	X	E	Z	1
Y	J	X	H	0
E	E	J	H	0
Z	H	X	J	0
H	Z	J	B	1
J	B	H	Z	1