5. Основные воздействия на объект управления. Нахождение передаточных функций по управлению, возмущению, для замкнутых и разомкнутых систем.

Задающее воздействие или входное воздействие х(t) – это воздействия которое планируется.

Управляющее воздействие (U(t)) – воздействие обусловлено управляющим уравнением и оказывает влияние на субъекты управления.

Внешнее воздействия f(t) – воздействие не планируемое, т.е. случайное (параметры окружающей среды). Выходное у(t) – управляемое переменной, данная величина характеризует параметры объекты управления. Внутреннее x(t) – обусловлено влиянием одних систем на другие.

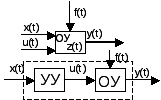
Передаточной функцией системы по управляющему воздействию называется отношение изображения выходной величины системы к изображению управляющего воздействия при нулевых начальных условиях.

Передаточная функция замкнутой системы по управляющему воздействию обозначается Ф(р). Она равна:

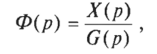
где Х{р) = L[x(t)] — изображение по Лапласу выходной величины замкнутой системы при нулевых начальных условиях; G(p) = Z,[g(/)] — изображение по Лапласу управляющего воздействия.

Передаточная функция разомкнутой системы по управляющему воздействию обозначается W (р). Она равна:

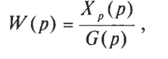
где Х_р(р) = L[x_p(t)] — изображение по Лапласу выходной величины разомкнутой системы при нулевых начальных условиях.

Передаточной функцией системы по возмущающему воздействию называется отношение изображения выходной величины системы к изображению возмущающего воздействия при нулевых начальных условиях.

Передаточная функция замкнутой системы по возмущающему воздействию обозначается У(р). Она равна:

где F{p) = ?[/(/)] — изображение по Лапласу возмущающего воздействия.

Передаточная функция разомкнутой системы по возмущающему воздействию обозначается V(р). Она равна:

При определении передаточных функций разомкнутых систем имеется в виду, что рассматривается поведение разомкнутой системы, у которой главная отрицательная обратная связь разомкнута.

6. Методика построения временных и частотных характеристик систем управления. Доделать

Временные и частотные характеристики однозначно связаны с уравнениями звеньев (и систем) и наряду с ними являются исчерпывающим описанием динамических свойств звеньев (и САУ в целом).

Временные характеристики представляют собой функции времени и служат для оценки динамических свойств элементов при их исследовании в плоскости действительного переменного t. К временным характеристикам относятся: переходная характеристика и импульсная переходная характеристика или ее еще называют весовая характеристика. Временные характеристики используются при описании линейных систем, как стационарных, так и нестационарных.

7 Типовые входные воздействия.

В качестве типовых задающих воздействий используют:

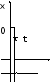
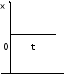
Рисунок 1 Типовые функции входного сигнала

1) единичное ступенчатое воздействие 1(t) – это функция, неизменная по величине и равная единице для всех моментов времени t>0, а при всех значениях t<0 равна 0. Например, подключение напряжения к звену или системе, начало обработки на станке, возмущение в виде ударов в механических системах и др.

Аналитически единичная функция может быть представлена таким образом:

1(t) =

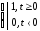
2) Дельта-функция 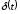– это функция Дирака, которая представляет собой импульс бесконечно большой амплитуды с бесконечно малой длительностью. Как правило, это шумы, помехи.

Аналитическая форма представления дельта-функции следующая:

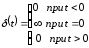
Между единичной ступенчатой функцией и дельта-функцией существует связь вида:

.

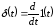3) Гармонический сигнал 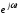– гармонические колебания с постоянной амплитудой, равной 1.

Этот сигнал может задаваться как в комплексной, так и в вещественной форме, в виде синусоидального или косинусоидального колебания:

,

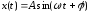
где А – амплитуда колебаний, равная 1. 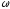– круговая частота, определяемая как , где Т – период; –начальная фаза.

Рассмотренные виды задающих воздействий имеют различное назначение. В случае применения единичного ступенчатого воздействия рассматривается переходной процесс, возникающий в элементе при переходе его из одного равновесного состояния в другое. Применение гармонического воздействия позволяет получить частотные характеристики системы.

Таким образом, в зависимости от применения определенного вида задающего воздействия динамические характеристики элементов можно разделить на два типа: временные характеристики, характеризующие свойства элементов в переходном режиме и частотные характеристики, отражающие свойства элементов в вынужденном движении.

8. Структурные схемы и их преобразования.

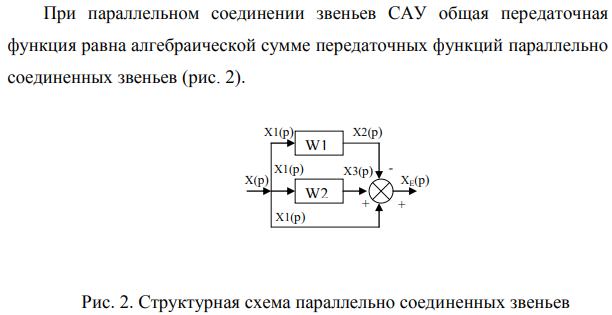
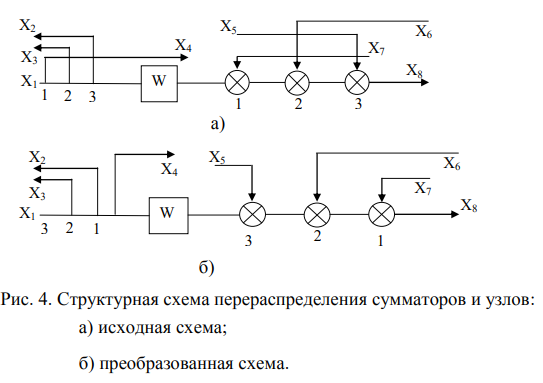
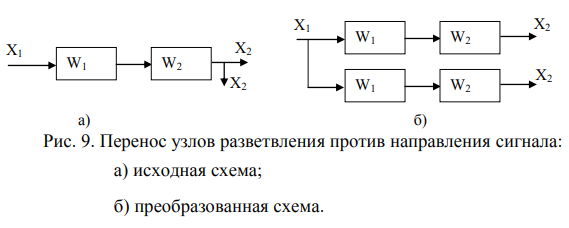
9. Непрерывные многомерные системы.

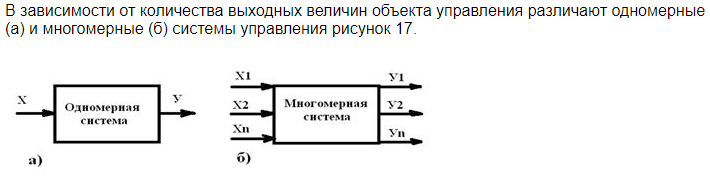
Система непрерывного действия состоит только из звеньев непрерывного действия, т.е. звеньев, выходная величина которых изменяется плавно и непрерывно при плавном изменении входной величины.