
- •1. Классификация сау.
- •2. Математические модели динамических систем.
- •Способы записи передаточных функций.
- •5. Основные воздействия на объект управления. Нахождение передаточных функций по управлению, возмущению, для замкнутых и разомкнутых систем.
- •6. Методика построения временных и частотных характеристик систем управления. Доделать
- •Непрерывная система, состоящая из непрерывных элементов и, имеющая несколько входных и выходных каналов, называется непрерывной многомерной системой.
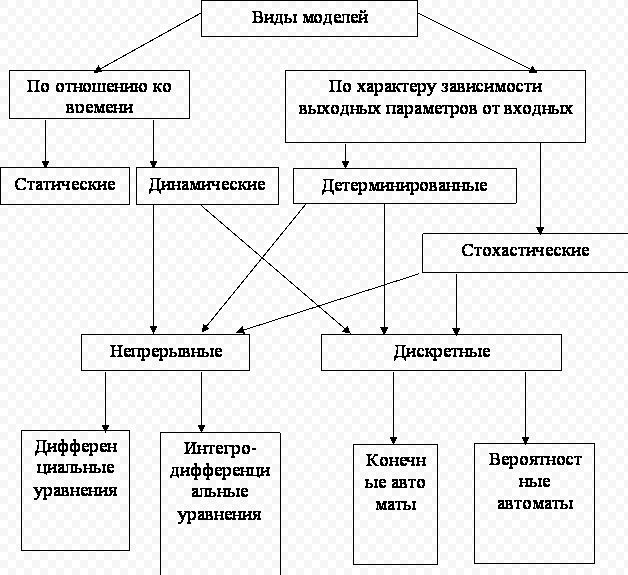
1. Классификация сау.
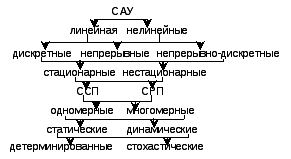
Линейные
системы –
системы которые описываются линейным
уравнением. Нелинейные
системы –
описываются нелинейными уравнениями,
т.е. дифференциальными. Непрерывные
системы –
состояние, которое задано на всем
непрерывном множестве. Дискретные
системы –
системы, значения выходной величины,
которая существует или определена в
конкретный момент времени
.
Непрерывно-дискретная
система, у которой выходная величина
на определенном участке представляет
собой непрерывную величину, и на
промежутке t1-t2
представляет собой дискретную величину.
Стационарные
системы –
системы, которые описываются уравнениями
с постоянными параметрами (параметры
не изменяются во времени). Нестационарные
– описываются уравнениями с переменными
параметрами. ССП
– системы с сосредоточенными параметрами
– системы, которые описываются
обыкновенными диф.уравнениями СРП
- диф.уравнениями в частных производных.
Одномерные
– системы, в которых выходная величина
одна![]() .
Многомерные
– имеют несколько выходных величин
.
Многомерные
– имеют несколько выходных величин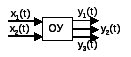 .
Статические
– без инерционные системы, т.е. постоянна
во времени
.
Статические
– без инерционные системы, т.е. постоянна
во времени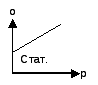 .
Динамические
– входная величина изменяется во
времени, для таких величин характерен
динамический процесс
.
Динамические
– входная величина изменяется во
времени, для таких величин характерен
динамический процесс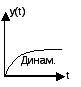 .
Детерминированные
– системы без внешних воздействий.
Стохастические
(вероятные или случайные)
– для таких систем характерно несколько
состояний и все она зависит от внешних
воздействий.
.
Детерминированные
– системы без внешних воздействий.
Стохастические
(вероятные или случайные)
– для таких систем характерно несколько
состояний и все она зависит от внешних
воздействий.
2. Математические модели динамических систем.
Динамические системы - системы, под действием внешних и внутренних сил изменяющие во времени свои состояния.
Математической моделью динамической системы принято называть совокупность математических символов, однозначно определяющих развитие процессов в системе, т.е. ее движение. При этом в зависимости от используемых символов различают аналитические и графоаналитические модели. Аналитические модели строятся с помощью буквенных символов, в то время как графоаналитические допускают применение графических обозначений.
Математическая модель динамической системы считается заданной, если введены параметры (координаты) системы, определяющие однозначно ее состояние, и указан закон эволюции. В зависимости от степени приближения одной и той же системе могут быть поставлены в соответствие различные математические модели.
В зависимости от степени приближения одной и той же системе могут быть поставлены в соответствие различные математические модели
3. Линейные динамические системы.

4. Передаточные функции систем. Формы записи передаточной функции.
Передаточная функция – это отношение выходного воздействия к входному воздействию при нулевых начальных условиях
Способы записи передаточных функций.
Для
исследования систем высокого порядка
используют операторный метод, который
основан на преобразованиях Лапласа и
который называется методом передаточных
функций системы. Передаточной функцией
системы или элемента называется отношение
выходной величины системы к входной
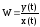 .
Существует 4 способа определения
передаточных функций:1)операторный
.
Существует 4 способа определения
передаточных функций:1)операторный
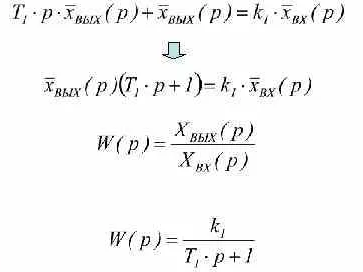 ;
2)стандартная форма
;
2)стандартная форма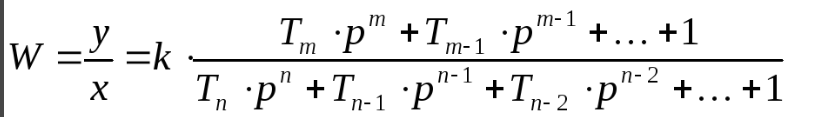
K- коэф. усиления системы
T-постоянные
времени;
3) частотная форма передаточной
функции степень
полинома знаменателя передаточной
функции называют порядком объекта
управления (системы), а разность между
степенями знаменателя и числителя
называют относительным порядком
передаточной функции;
4)
передаточной функции в изображениях
по Лапласу.
степень
полинома знаменателя передаточной
функции называют порядком объекта
управления (системы), а разность между
степенями знаменателя и числителя
называют относительным порядком
передаточной функции;
4)
передаточной функции в изображениях
по Лапласу.

