2.2.5. Тренд-анализ

Длительная (вековая) тенденция изменения экономических показателей. Когда строятся экономико-математические модели прогноза, тренд оказывается основной составляющей прогнозируемого временного ряда, на которого накладывается другие составляющие (сезонные, цикличные колебания и др.).

Тренд-модель – динамическая модель, где развитие экономической системы отражается через тренд основных показателей (средних величин, дисперсий, min-max уровней рядов).

В тренд-анализе имеет место рассмотрение рядов динамики (временных рядов). Временной ряд – ряд расположенных во времени статистических показателей, характеризующих изменение данного общественного явления (рис. 3).

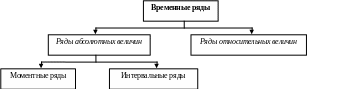
Рис. 3. Классификация временных рядов

Моментный временнóй ряд – ряд абсолютных величин, характеризующих уровень изучаемого явления (y) на определенный момент времени (t), – y_t.

Интервальный временнóй ряд – ряд абсолютных величин, характеризующих уровни изучаемого явления (y) на определенные периоды времени (t), – y_t.

Показатели анализа временнóго ряда:

• абсолютный прирост: S_t = y_t – y_{t – 1}; (66)

• абсолютный прирост базисный:

Δy_б = y_t – y₀; (67)

• абсолютный прирост цепной:

Δy_ц = y_t – y_{t – 1}; (68)

• темп роста: T_рt = y_t / y_{t – 1}; (69)

• темп роста базисный: Т_р^б = y_t / y₀ • 100%; (70)

• темп роста цепной: Т_р^ц = y_t / y_{t – 1} • 100%; (71)

• темп роста средний:

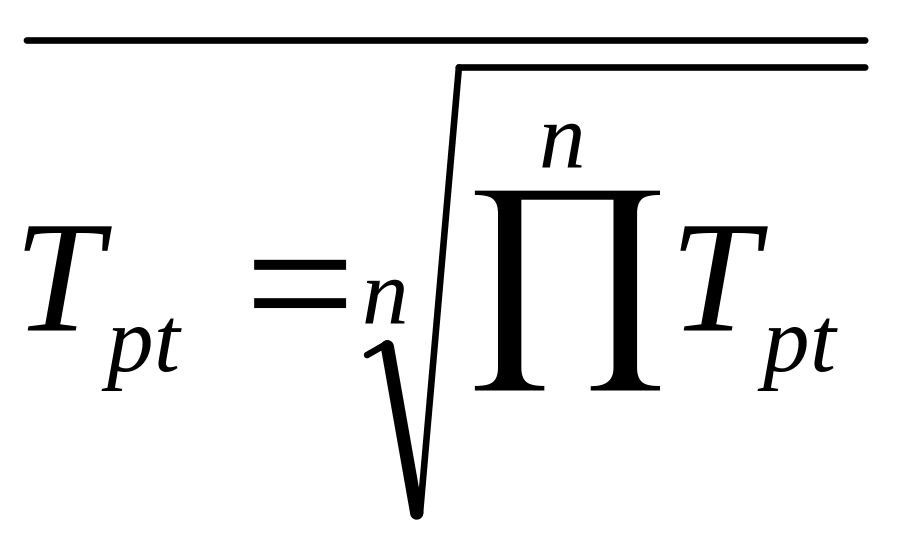, (72)

• темп прироста: T_прt = T_рt – 1; (73)

• темп прироста средний:

; (74)

• абсолютное значение 1% прироста:

A_т = 0,01 • y_{t – 1} . (75)

Средний уровень интервального ряда:

, (76)

где n – число периодов времени.

Средний абсолютный прирост:

, (77)

где n – число приростов.

Для моделирования временнóго ряда целесообразно случайные социально-экономические процессы разбить на систематическую составляющую, являющуюся детерминированной и связанной с ходом времени (t), и случайную компоненту (ε_t) – остаток:

y_t = f(t) + ε_t. (78)

Количественное описание тенденции может быть выполнено с помощью различных методов:

• метод скользящей средней – нахождение центрированных значений средних скользящего интервала. Сглаженный ряд короче первоначального на (К – 1) уровней при ширине избранного интервала (К);

• метод аналитического выравнивания – фактические уровни временнóго ряда заменяются теоретическими на основе линейной или нелинейной формы связи. В качестве факторного анализа принимается время. Тенденция временнóго ряда представлена некоторым уравнением регрессии:

• авторегрессионная модель временнóго ряда – авторегрессия первого и высших порядков;

• непосредственное коррелирование временнóго ряда;

• коррелирование остатков временнóго ряда;

• коррелирование временнóго ряда, учитывая время как фактор.

Фактическое значение уровня временнóго ряда:

y_t = a₀ + a₁ • y_{t – τ} + ε_t. (79)

При авторегрессии высших порядков (многофакторной) данные автокорреляционной функции говорят о высокой степени тесноты связи уровней временнóго ряда нескольких последовательных сдвигов. Независимыми факторными признаками в ней будут выступать уровни явления нескольких предыдущих периодов.

Уравнение авторегрессии с тремя факторными признаками (3-го порядка) имеет вид:

ŷ_t = a₀ + a₁ • y_{t – 1} + a₂ • y_{t – 2} + a₃ • y_{t – 3}. (80)

При непосредственном коррелировании временнóго ряда колебания этих рядов часто бывают взаимообусловлены. К коррелированию остатков временнóго ряда прибегают, когда непосредственная их корреляция связана с искажениями. Пусть тренды рядов (y_t) и (x_t) представлены аналитическим способом, тогда значения их остатков выразятся как:

ε_t = y_t – f(t) (для ряда – y_t), (81)

μ_t = x_t – φ(t) (для ряда – x_t). (82)

Полученное значение коэффициента корреляции признаков, вычисленное по остаткам r, дает неискаженное представление о степени тесноты их связи:

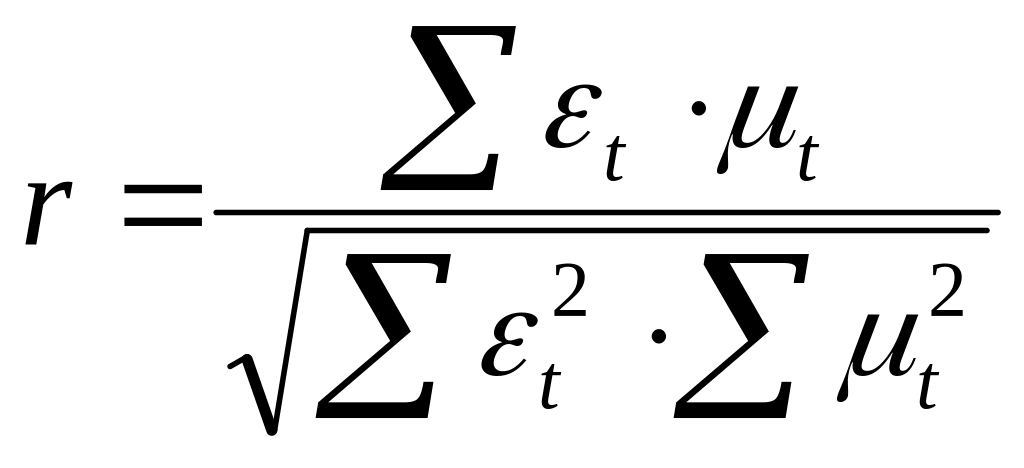. (83)

При включении времени как фактора в корреляционное уравнение регрессии устраняется эффект влияния тренда. Так, динамическая зависимость двух рядов может быть представлена следующим образом:

y_t = a₀ + a₁ • x₁ + a₂ • t. (84)

Важной задачей тренд-анализа является изучение изменений анализируемых данных по определенному кругу показателей. Для этого можно использовать динамический ряд (ряд динамики).

Ряд динамики – ряд расположенных в хронометрической последовательности числовых значений статистического показателя, который характеризует изменение признака во времени, т.е. исследование значений во временной последовательности. Он характеризуется:

• показателем периода времени;

• показателем объекта за этот период времени (уровень ряда).

Различают моментный и интервальный ряды динамики.

Моментный ряд динамики – ряд, где приведены данные о размере явления на определенную дату или момент времени. Моментные ряды не суммируются, т.к. в каждом последующем уровне содержится полностью или частично значение предыдущего уровня.

Интервальный ряд динамики – ряд, где приведены данные о размере явления за определенный период времени. Интервальные ряды можно суммировать, в результате получается уровень ряда более продолжительного периода.

Основным условием правильности построения динамического ряда является сопоставимость уровней ряда между собой, т.е. статистические данные должны быть сопоставимы по кругу исследуемых объектов, времени, места анализа, методов расчета, ценам и др.

Показатели (абсолютный прирост, темп роста, темп прироста, абсолютное значение одного процента прироста) рассчитываются по постоянной (относительно базисного, т.е. начального уровня) и переменной (каждый последующий уровень сравнивают с предыдущим) базам сравнения. Вычисленные таким образом показатели анализа динамики называются соответственно базисными и цепными.