3. Анализ затрат:

• стоимостной индекс затрат: 9 973 372 / 8 366 132 = 1,192;

• себестоимость единицы продукции: 9 973 372 / 9 192 102 = 1,085;

• индекс физического объема затрат: 9 192 102 / 8 366 132 = 1,099, проверка: 1,085 • 1,099 = 1,192;

• общие изменения издержек: 9 973 372 – 8 366 132 = 1 607 240;

• изменение затрат за счет изменения себестоимости единицы продукции: 9 973 372 – 9 192 102 = 781 270;

• изменение затрат за счет изменения физического объема: 9 192 102 – 8 366 132 = 825 970, проверка: 781 270 + 825 970 = 1 607 240.

Выводы:

• стоимость затрат повысилась на 19,2% (119,2% – 100%);

• себестоимость единицы затрат повысилась на 8,5% (108,5% – 100%);

• физический объем затрат вырос на 9,9% (109,9% – 100%).

4. Анализ цен:

• индекс переменного состава:

13 432 000 • 12 948 / (12 000 920 • 13 020) = 1,113;

• индекс фиксированного состава: 13 432 000 / 12 325 600 = 1,09;

• индекс структурных сдвигов: 1,113 / 1,09 = 1,021.

Выводы:

• средняя цена выросла за счет изменения средней цены на 11,3% (111,3% – 100%);

• средняя цена выросла за счет изменения общего роста цен на 9% (109% – 100%).

5. Анализ производительности (эффективности):

• общий индекс производительности: 1,119 / 1,192 = 0,939;

• индекс ценового опережения: 1,09 / 1,085 = 1,005;

• индекс производительности в физическом выражении: 1,027 / 1,099 = 0,934.

Выводы:

• общая производительность снизилась на 6,1% (100% – 93,9%);

• опережение результатов над затратами, связанных с ростом цен вырос на 0,5% (100,5% – 100%);

• производительность в физическом объеме снизился на 6,6% (100% – 93,4%).

6. Анализ прибыли:

• общий индекс прибыли: (13 432 000 – 9 973 372) / (12 000 920 – 8 366 132) = 0,096;

• индекс роста прибыли за счет роста объема продукции:

(12 325 600 – 9 192 102) / (12 000 920 – 8 366 132) = 0,86;

• индекс роста прибыли за счет роста цен: (13 432 000 – 9 973 372) / (12 325 600 – 9 192 102) = 0,111.

Выводы:

• общая прибыль снизилась на 90,4% (100% – 9,6%);

• рост прибыли за счет роста объема продукции снизился на 14% (100% – 86%);

• рост прибыли за счет роста цен уменьшился на 88,9% (100% – 11,1%).

7. Анализ дополнительной прибыли:

• общая экономия с учетом роста объема производства и снижения цен на издержки производства: 8 366 132 • 1,119 – 9 973 372 = – 611 670,3;

• эффективность (неэффективность) использования той или иной статьи затрат: 8 366 132 • 1,027 – 9 973 372 = – 1 381 354,4;

• соотношение цен на материалы и продукцию:

– 611 670,3 – (– 1 381 354,4) = 769 684,1.

Выводы:

• общей экономии с учетом роста объема производства и снижения цен на издержки производства нет;

• неэффективность использования той или иной статьи затрат равна – 1 381 354,4;

• соотношение цен на материалы и продукцию равно 769 684,1.

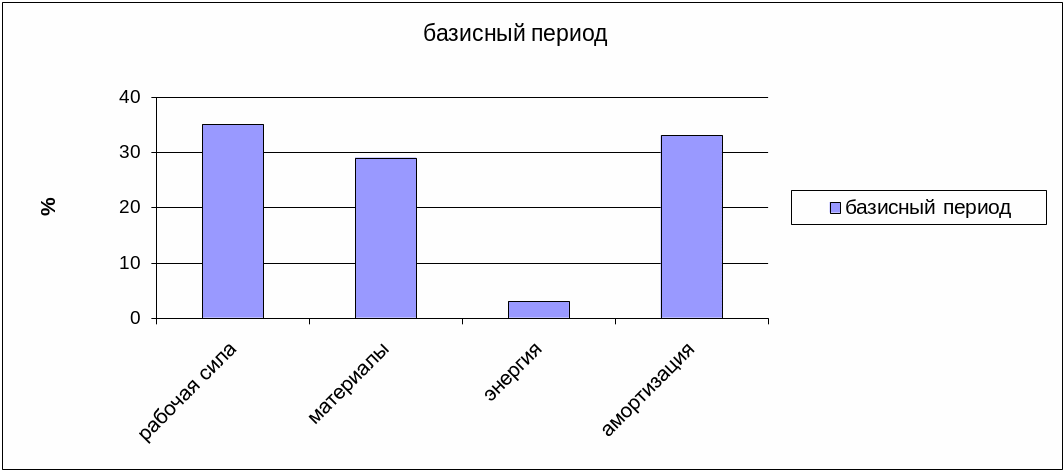
Диаграмма 1. Базисный период

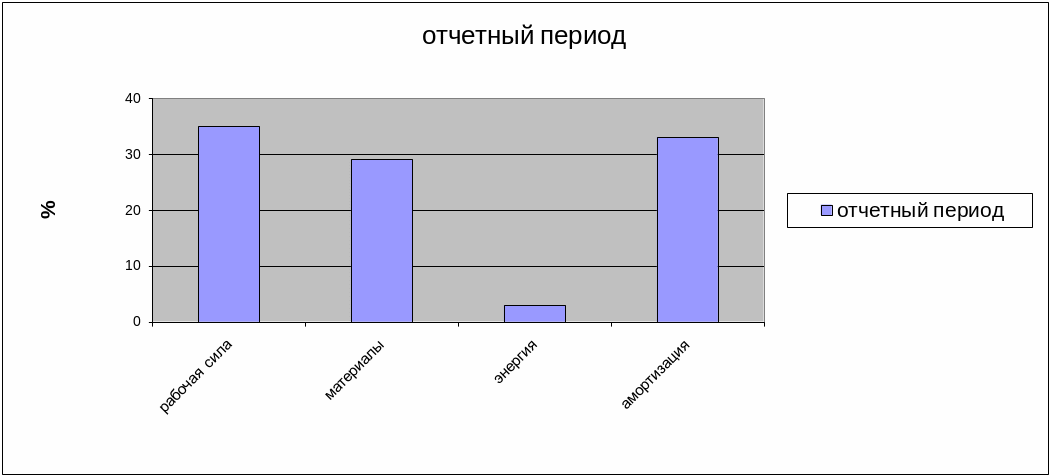
Диаграмма 2. Отчетный период

Задачи для решения.

Задача 2.2.4.а. Предприятие изготовляет продукцию трех видов. Определить по исходным данным, приведенным в таблице:

- индивидуальные индексы себестоимости по каждому изделию;

- процент снижения по каждому изделию;

- общий индекс;

- агрегатный индекс и средние из индивидуальных индексов.

Сделать соответствующие аналитические выводы.

Изделие	Себестоимость продукции, руб.		Количество продукции (тыс. ед.)
	Базисный период	Отчетный период
А	150	138	100
Б	40	48	20
В	40	40	50

Задача 2.2.4.б. По исходным данным о продажах и ценах на изделия, приведенным в таблице, определить:

• общее изменение физического объема продаж;

• общее изменение цен на указанные продукты;

• абсолютную экономию населения от снижения цен;

• общий индекс цен (Ласперейса, Пааше, Лоу).

Сделать аналитические выводы.

Продукт	Единица измерения	Продано, тыс. шт.		Цена единицы, руб.
		базисный период	отчетный период	базисный период	отчетный период
А	кг	60	70	30	25
Б	кг	50	60	20	15
В	кг	2,5	3,0	200	180

Задача 2.2.4.в. Имеются следующие данные об уровне заработной платы работников предприятия и розничных ценах на товары. Определить:

• индекс номинальной заработной платы;

• индекс розничных цен на товары потребительской корзины;

• индекс реальной заработной платы.

Категории работников	Заработная плата, тыс. руб./мес.		Розничная цена на товары потребительской корзины
	базисный период	текущий период	базисный период	текущий период
Рабочие	15,5	16,5	3,8	4,5
Служащие	14,5	15,0
Специалисты	26,0	27,0
МОП	9,0	9,2

Задача 2.2.4.г. В базисном году месячная заработная плата составила 17,5 тыс. руб., в текущем году – 18,9 тыс. руб. За это время розничные цены на платные услуги повысились в целом на 15%. Определить:

• индекс номинальной и реальной заработной платы;

• изменение реального содержания заработной платы.

Задача 2.2.4.д. Имеются следующие данные об изменении численности рабочих в геологической организации в процентах к предыдущему году. Определить, на сколько процентов увеличилось число рабочих на заводе за 5 лет.

1 год	2 год	3 год	4 год	5 год
+ 8	+ 7	+ 10	+ 8	+ 9

Тестовые задания.

1. Установите соответствие перечисленных видов индексов их содержанию:

   Вид индекса	Содержание индекса
   1. Индивидуальный	А. Индекс выражает сводные или обобщенные результаты совместного изменения по всей совокупности элементов сложного экономического явления.
   2. Общий	Сопоставление текущих уровней с предшествующим, т.е. база сравнения непрерывно меняется.
   3.Базисный	В. Индекс, характеризующий изменение только одного элемента совокупности.
   4. Цепной	Г. Индекс получают сопоставлением с уровнем какого-то одного определенного периода.

2. Индекс стоимости продукции вычисляется по формуле:

а) ; б) ; в) .

3. Данная система индексов стоимости – цепная (а) или базисная (б)?

; ; … .

4. Индекс цен Ласперейса определяется по формуле:

а) ; б) ; в) .

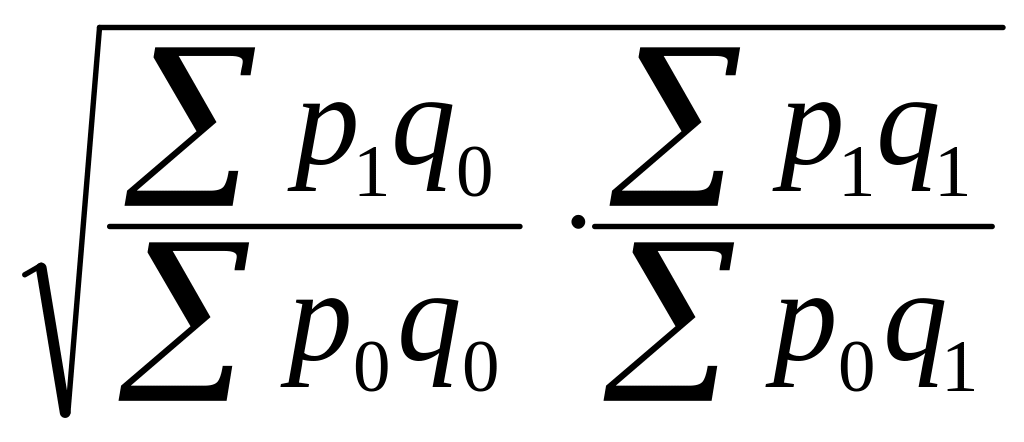4. Индекс Пааше определяется по формуле:

а) ; б) ; в) .

4. Индекс Лоу определяется по формуле:

а) ; б) ; в) .

4. Индекс количества продукции, произведенной в единицу времени, рассчитывается по формуле:

а) ; б) ; в) ; г) .

4. Допишите ответ вместо прочерка.

Формула агрегатного индекса физического объема позволяет определить не только относительное, но и ______________________ изменение физического объема.

4. Допишите ответ вместо прочерка.

Отношение фактической стоимости продукции отчетного периода к стоимости объема продукции, структура которого аналогична структуре отчетного года, но определенного в ценах базисного года, называется индексом ______________________.