2.2.3. Элементарные методы обработки расчетных данных

При изучении совокупности значений изучаемых величин, помимо средних, используют и другие характеристики. При анализе больших массивов данных обычно интересуются двумя аспектами: во-первых, величинами, характеризующими ряд значений как целого, т.е. характеристиками общности; во-вторых, величинами, описывающими различия между членами совокупности, т.е. характеристиками разброса (вариации) значений.

Размах вариации рассчитывается по формуле:

R = x_max – x_min (17)

Среднее линейное отклонение (средний модуль отклонения) от среднего арифметического вычисляется по формуле:

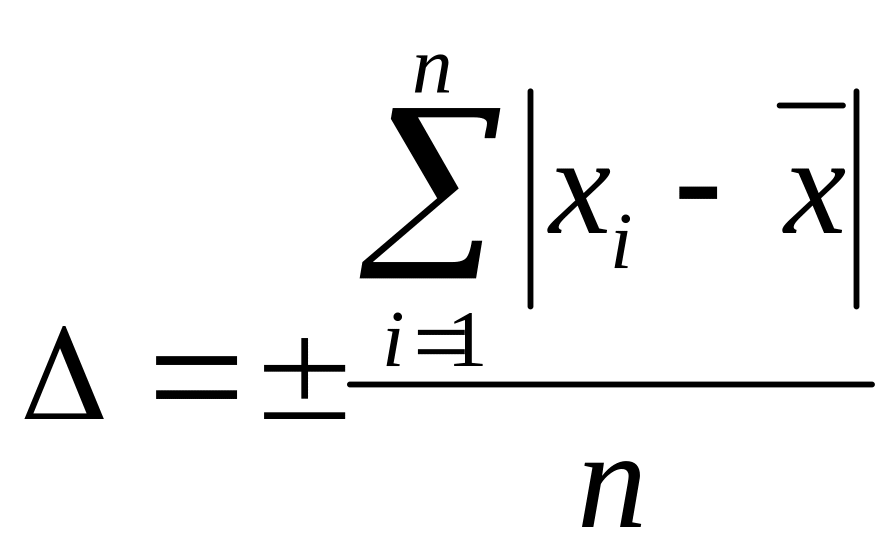(18)

Если используются весовые коэффициенты, то формула среднеквадратического отклонения имеет вид:

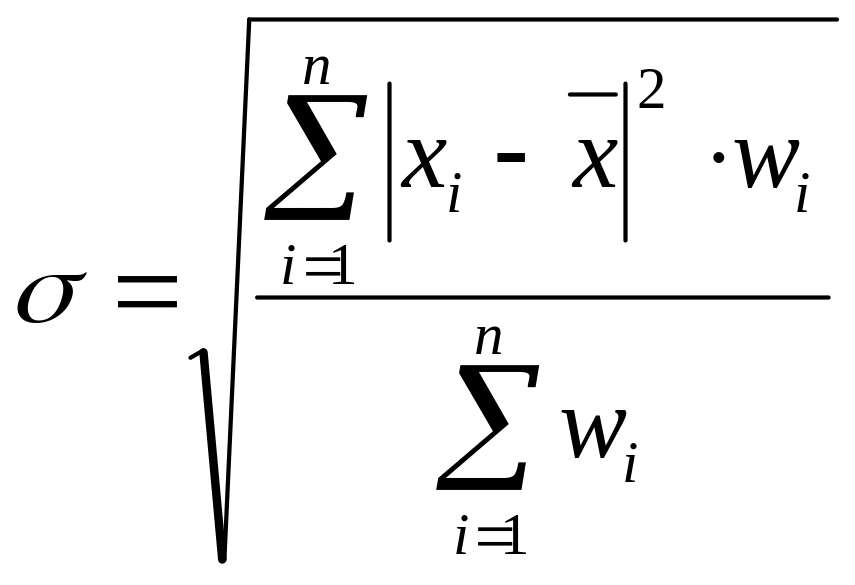, (19)

где: w_i – частота, с которой в изучаемой совокупности встречается значение x_i.

Наибольшее распространение при изучении разброса значений числовых данных получили величины среднеквадратического отклонения (СКО) σ и дисперсии σ².

Для сравнения рядов данных, отличающихся по абсолютным величинам, вводят коэффициент вариации (V_Δ, V_σ):

, (20)

. (21)

2.2.4. Индексный метод

Мощным орудием сравнительного анализа экономики являются индексы. Индекс – статистический показатель, отношение двух состояний какого-либо признака. C помощью индексов проводятся сравнения с планом, в динамике, в пространстве.

Простой (частный, индивидуальный) индекс – это индекс, при котором исследуемый признак берется без учета связи его с другими признаками изучаемых явлений. Простой индекс имеет вид:

, (22)

где p₁ и p₀ – сравниваемые состояния признака.

Аналитический (общий, агрегатный) индекс – индекс, когда исследуемый признак берется не изолированно, а в связи с другими признаками. Он состоит всегда из двух компонент: индексируемый признак (p) (тот, динамика которого исследуется) и весовой признак (q). С помощью признаков-весов измеряется динамика сложного экономического явления, отдельные элементы которого несоизмеримы.

Простые и аналитические индексы дополняют друг друга:

, (23)

где q₀ или q₁ – весовой признак.

Индексный анализ – анализ изменения качественных и количественных показателей текущего (отчетного) периода по базисному. В зависимости от характера изучаемого явления вычисляются индексы объемных и качественных показателей. Индексы качественных показателей характеризуются изменением цен, издержек обращения, производительности труда, прибыли, себестоимостью товарооборота. Основой индексного метода является переход от натуральной вещественной формы выражения к стоимостным измерениям. Посредством денежного выражения стоимости отдельных товаров устраняется независимость некоторых показателей и достигается единство.

Существующая классификация индексов приведена на рис. 2.

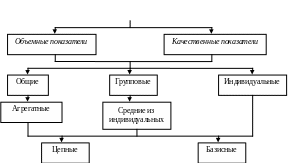
Индексы

Рис. 2. Классификация индексов

Индивидуальные индексы:

• индекс физического объема продукции:

, (24)

где q₁, q₀ – количество продаж товаров в текущем и базовом периодах соответственно;

• индекс цен:

, (25)

где p₁, p₀ – цены за единицу товара в текущем и базисном периодах соответственно;

• индекс изменения объема затрат:

, (26)

где z₁, z₀ – себестоимость единицы продукции в отчетном и базисном периодах соответственно;

• индекс трудоемкости:

, (27)

где t₁, t₀ – затраты времени на производство единицы продукции в отчетном и базисном периодах соответственно;

• индекс стоимости: pq = p₁q₁ / p₀q₀; (28)

• индекс стоимости данной продукции:

i_c = с₁/с₀; (29)

• индекс издержек производства:

i_cz = c₁z₁ / c₀z₀. (30)

Агрегатные индексы позволяют перейти от натуральных измерений разнородных величин к однородным:

• общий индекс стоимости продукции:

I_pq = Σp₁q₁ / Σp₀q₀; (31)

• индекс цен:

I_p = Σp₁q₁ / Σp₀q₁; (32)

• общий индекс физического объема продукции:

I_q = Σp₀q₁ / Σp₀q₀. (33)

Связь индексов: I_pq = I_p • I_q. (34)

• Общие изменения стоимости продукции:

ΔPQ = Σp₁q₁ – Σq₀p₀; (35)

• общие изменения стоимости продукции за счет изменения цен:

ΔP_q = Σp₁q₁ – Σp₀q₁; (36)

• общие изменения стоимости продукции за счет изменения физического объема:

ΔQ_p = Σp₀q₁ – Σp₀q₀ . (37)

Связь индексов: ΔPQ = ΔP_q + ΔQ_p. (38)

• Стоимостной индекс затрат:

I_cz = Σc₁z₁ / Σc₀z₀; (39)

• индекс себестоимости единицы затрат:

I_c = Σc₁z₁ / Σc₀z₁; (40)

• индекс физического объема затрат:

I_z = Σc₀z₁ / Σc₀z₀. (41)

Связь индексов: I_cz = I_c + I_z. (42)

• Общие изменения издержек:

ΔCZ = Σc₁z₁ – Σc₀z₀; (43)

• изменения затрат за счет изменения себестоимости единицы продукции:

ΔC_z = Σc₁z₁ – Σc₀z₁; (44)

• изменения затрат за счет изменения физического объема продукции:

ΔZ_c = Σc₀z₁ – Σc₀z₀. (45)

Связь индексов: ΔCZ = ΔC_z + ΔZ_c. (46)

Индекс Пааше характеризует влияние изменения цен на стоимость товаров в отчетном периоде:

, (47)

где Σp₁q₁ – сумма стоимости продаж товара в текущем периоде по текущим ценам; Σp₀q₁ – сумма стоимости продаж товара в текущем периоде по базисным ценам.

Индекс Ласперейса показывает влияние изменения цен на стоимость количества товаров, реализуемых в базисном периоде:

. (48)

Индекс Лоу – средние величины реализации товаров за два и более периодов:

. (49)

. (50)

Индекс изменения физического объема товарной массы:

, (51)

где q₁, q₀ – цены базисного периода.

Индекс плановой реализации:

. (52)

Связь индексов:

I_qp = I_q • I_p. (53)

• Индекс переменного состава (фиксирует изменения средней цены):

I_пер = (Σp₁q₁ • Σq₀) / (Σp₀q₀ • Σq₁); (54)

• индекс фиксированного состава (фиксирует изменения средней цены за счет общего роста цен):

I_ф = Σp₁q₁ / Σp₀q₁; (55)

• индекс структурных сдвигов:

I_{стр. сдв} = I_пер / I_ф; (56)

• общий индекс производительности:

I_пр = I_pq / I_cz; (57)

• индекс ценового опережения:

I_rec = I_p / I_c; (58)

• индекс производительности в физическом выражении:

I_r = I_q / I_z; (59)

• общий индекс прибыли:

I_пр = (Σp₁q₁ – Σc₁z₁) / (Σp₀q₀ – Σc₀z₀); (60)

• индекс роста прибыли за счет роста объема продукции:

I^q_пр = (Σp₀q₁ – Σc₀z₁) / (Σp₀q₀ – Σc₀z₀); (61)

• индекс роста прибыли за счет изменения роста цен:

I^p_пр = (Σp₁q₁ – Σc₁z₁) / (Σp₀q₁ – Σc₀z₁); (62)

• общая экономия с учетом роста объема производства и снижения цен на издержки производства:

ΔR = Σc₀z₀ • I_pq – Σc₁z₁; (63)

• эффективность (неэффективность) использования той или иной статьи затрат:

ΔE = Σc₀z₀ • I_q – Σc₁z₁; (64)

• соотношение цен на материалы:

ΔREC = ΔR – ΔE. (65)