
- •Часть 2
- •§3. Линейные дифференциальные уравнения
- •3.1. Линейно независимые функции
- •3.2. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •3.3. Линейные неоднородные дифференциальные уравнения (лнду) второго порядка
- •§ 4. Системы дифференциальных уравнений
- •4.1. Нормальные системы дифференциальных уравнений
- •4.2. Система линейных дифференциальных уравнений с постоянными коэффициентами.
- •4.3 Линейные неоднородные системы
- •394026 Воронеж,
4.3 Линейные неоднородные системы
Нормальная линейная неоднородная система дифференциальных уравнений имеет вид
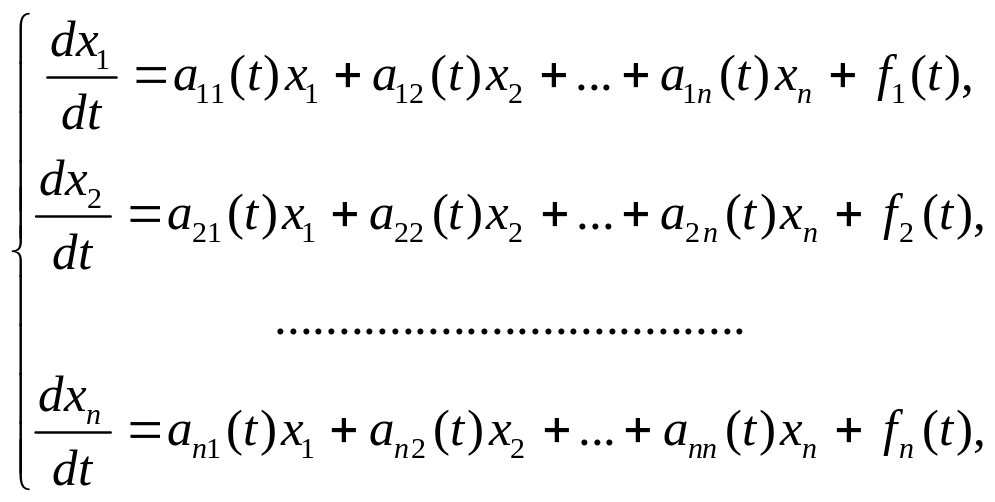
где по крайней мере одна из функций
![]() не равна нулю тождественно.
не равна нулю тождественно.
Эту систему можно записать в виде одного матричного дифференциального уравнения
![]()
где
![]() .
Интегрирование системы можно проводить
методом исключения, однако предпочтительнее
найти предварительно решение
.
Интегрирование системы можно проводить
методом исключения, однако предпочтительнее
найти предварительно решение
![]() соответствующей однородной системы
соответствующей однородной системы
![]() и какое-либо частное решение
и какое-либо частное решение
![]() неоднородной системы. Тогда общее
решение неоднородной системы имеет вид
неоднородной системы. Тогда общее
решение неоднородной системы имеет вид
![]() .
.
Если известна фундаментальная система
![]() ,
решений однородной системы, то общее
решение
,
решений однородной системы, то общее
решение
![]() можно найти методом вариации произвольных
постоянных, полагая
можно найти методом вариации произвольных
постоянных, полагая
![]()
Определяем функции
![]() подстановкой в неоднородную систему.
Учитывая при этом равенства
подстановкой в неоднородную систему.
Учитывая при этом равенства
![]()
приходим к системе уравнений относительно
![]() .
Из этой системы находим
.
Из этой системы находим
![]() и интегрируя, получаем функции
с точностью до произвольных постоянных.
Подставляя их в равенство
,
получаем искомое общее решение неодно-
и интегрируя, получаем функции
с точностью до произвольных постоянных.
Подставляя их в равенство
,
получаем искомое общее решение неодно-
родной системы.
Решить линейные однородные системы с постоянными коэффициентами:
1.
![]() 2.
2.
![]() 3.
3.
![]()
4.
![]() 5.
5.
![]() 6.
6.
![]()
7.
![]() 8.
8.
![]() 9.
9.
![]()
10.
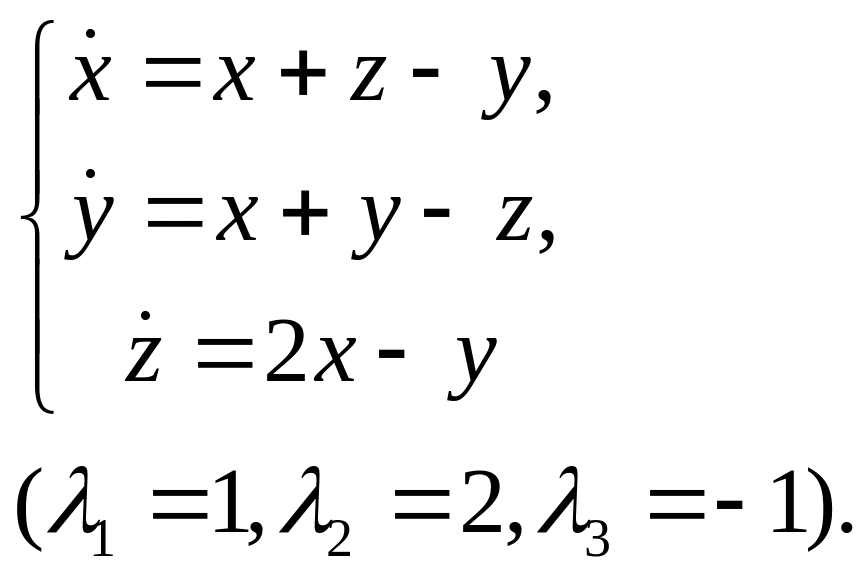 11.
11.
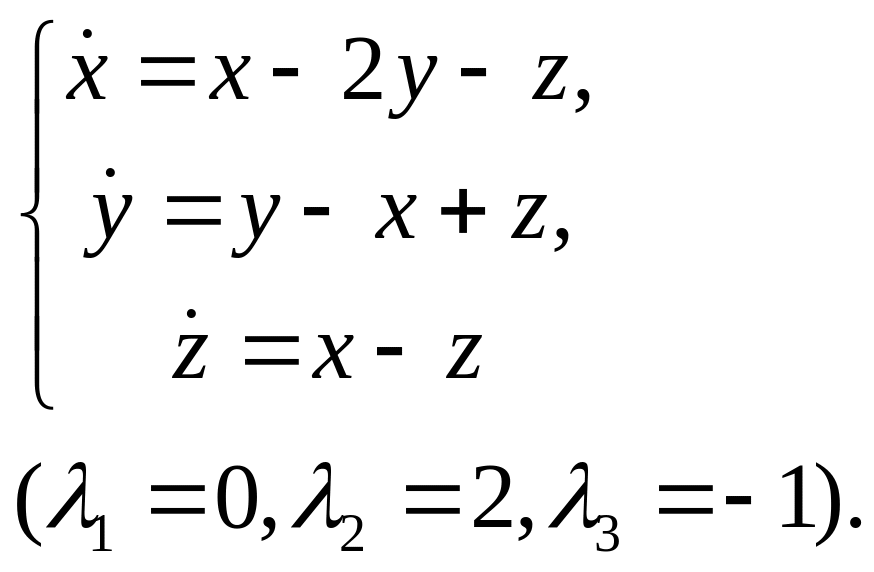
12.
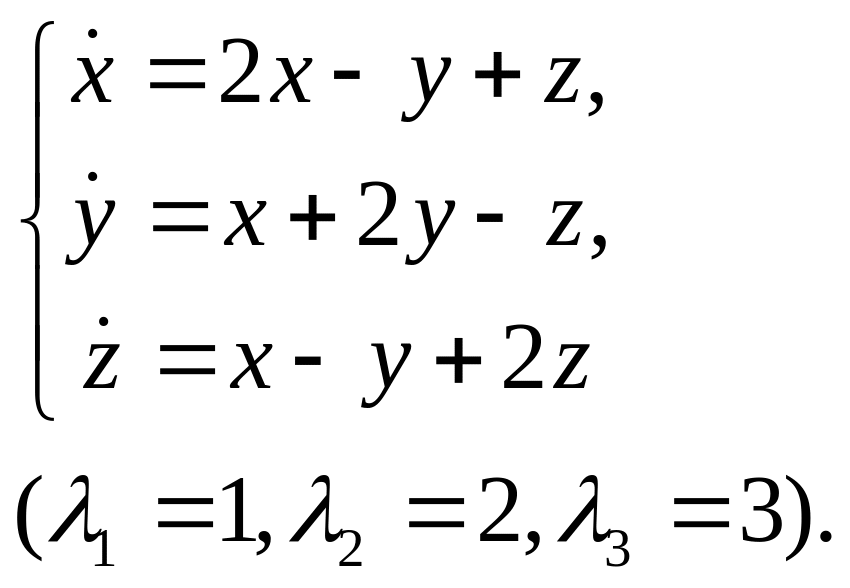 13.
13.

14.
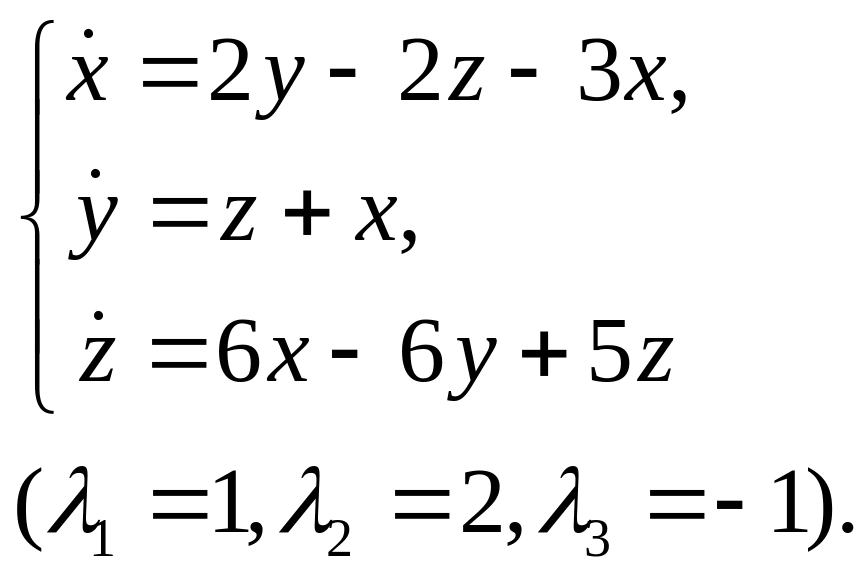 15.
15.
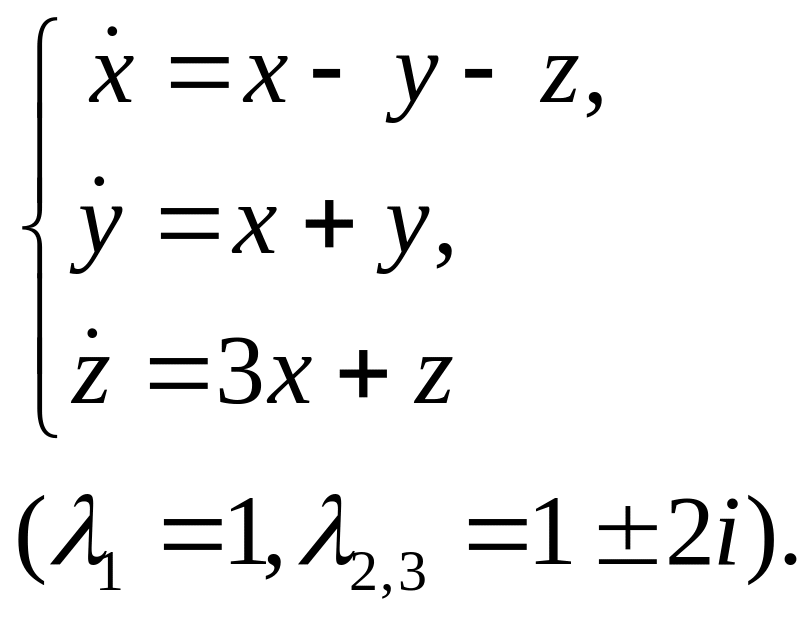
16.
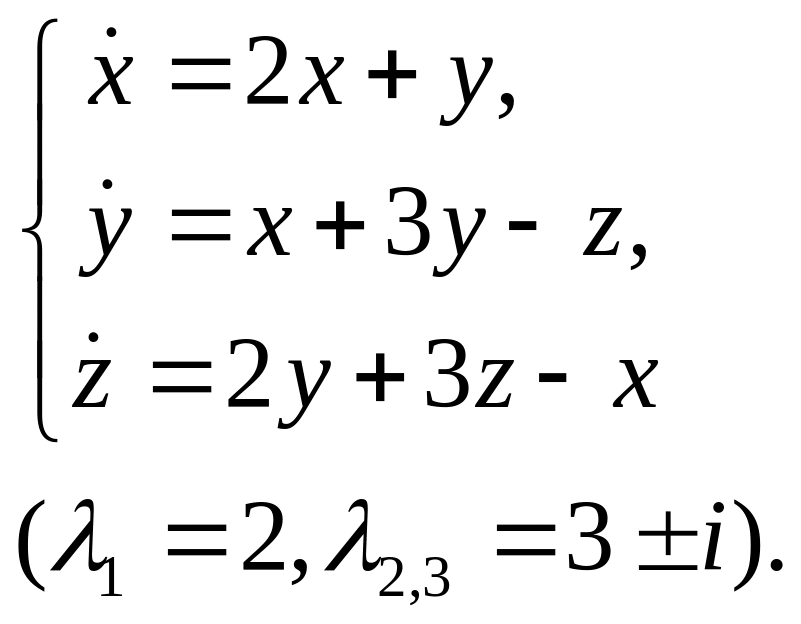 17.
17.
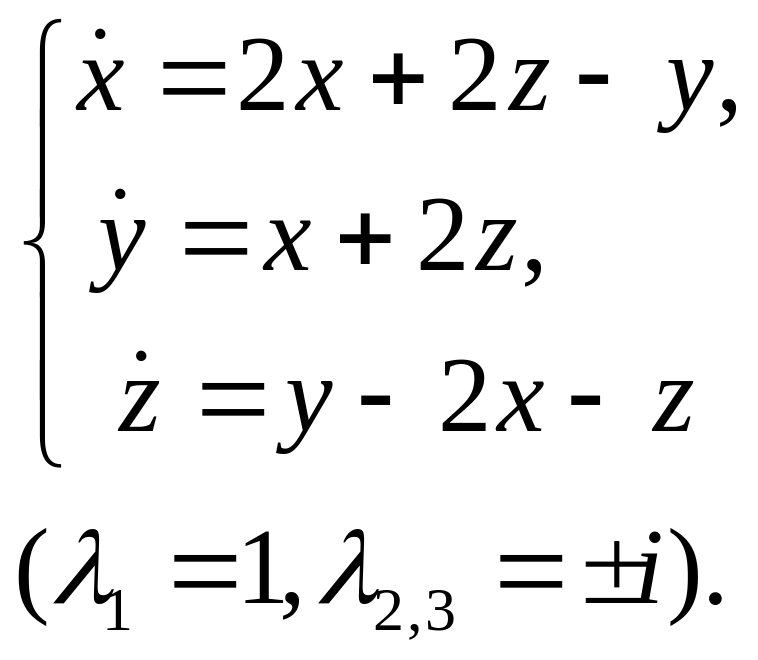
18.
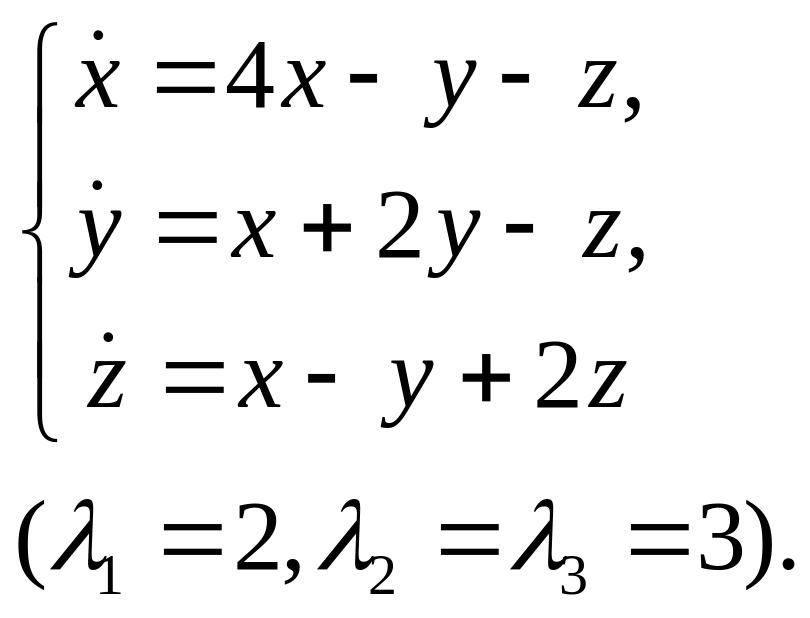 19.
19.
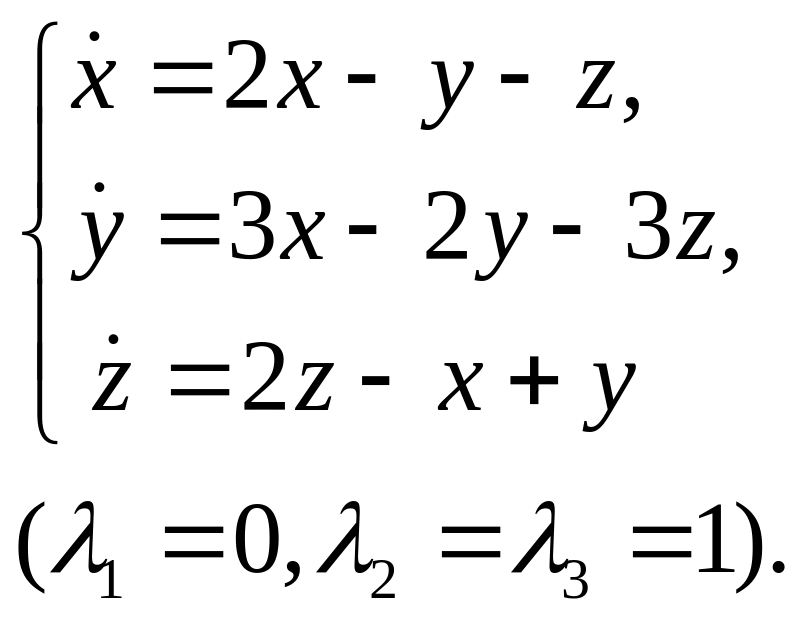
20.
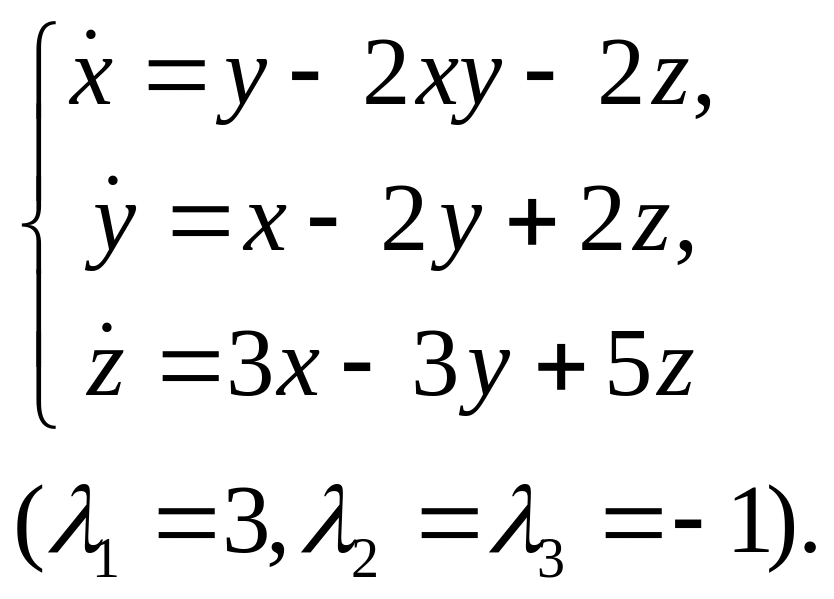 21.
21.
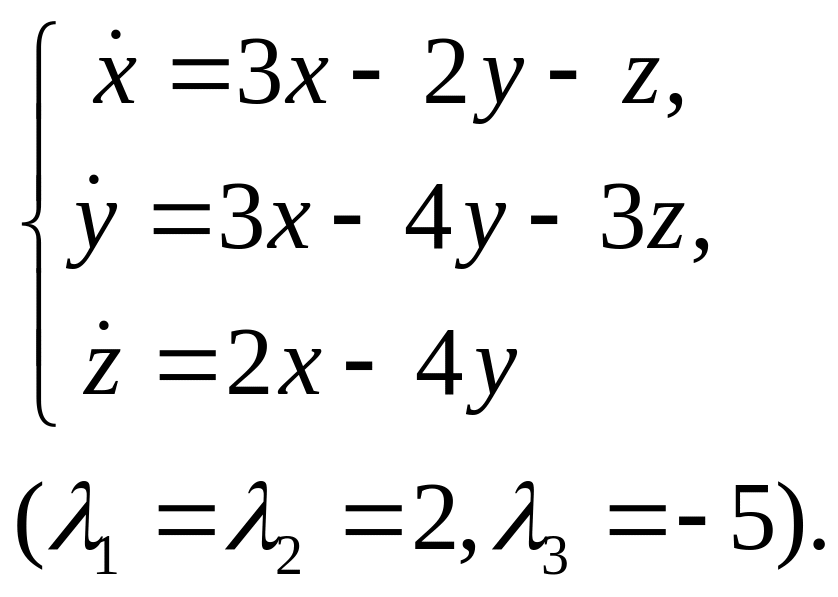
22.
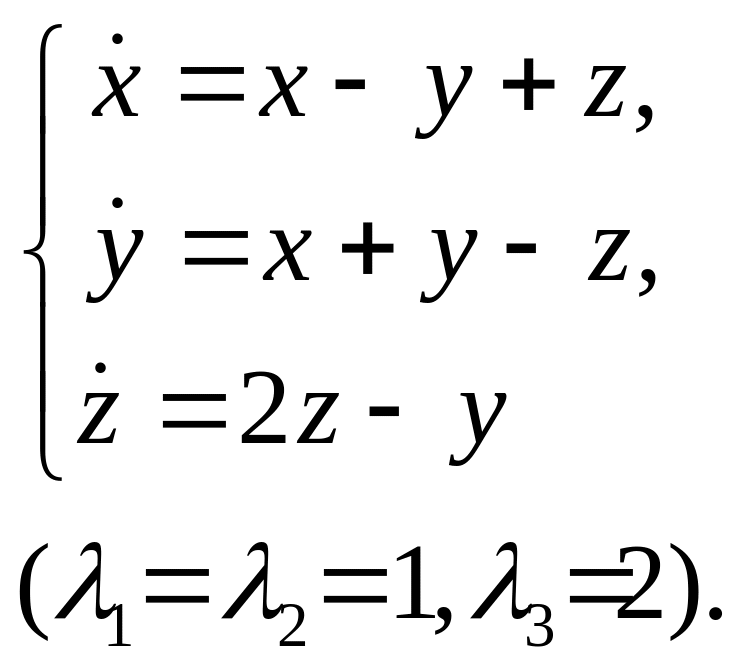 23.
23.
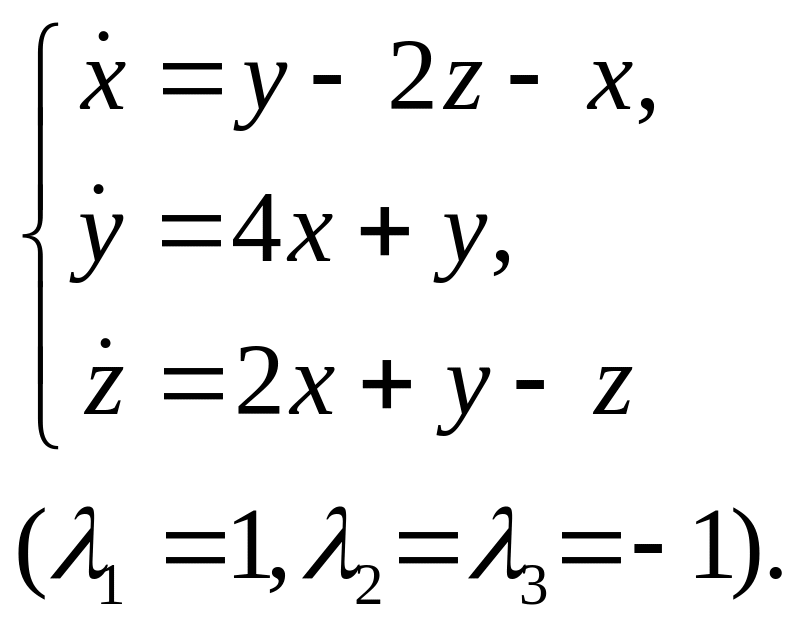 24.
24.
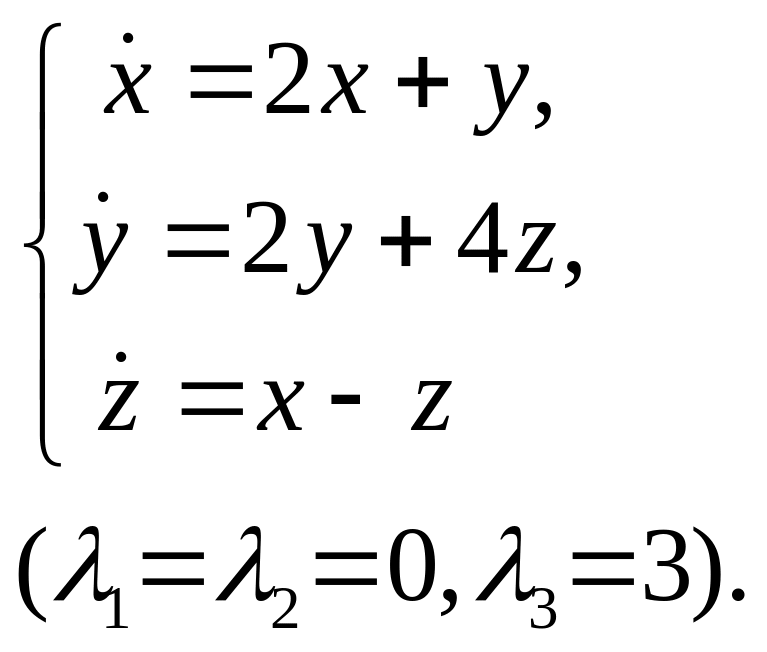
Решить линейные неоднородные системы:
25.
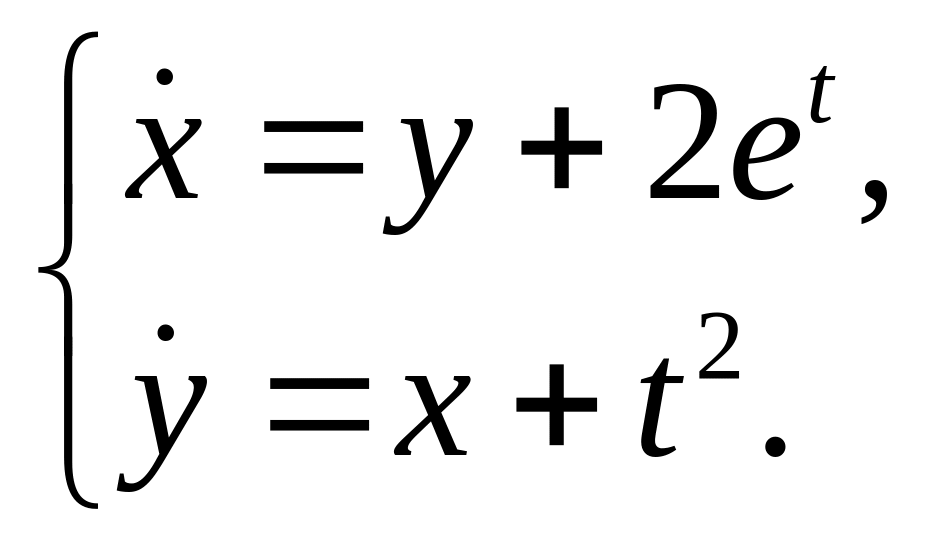 26.
26.
![]() 27.
27.
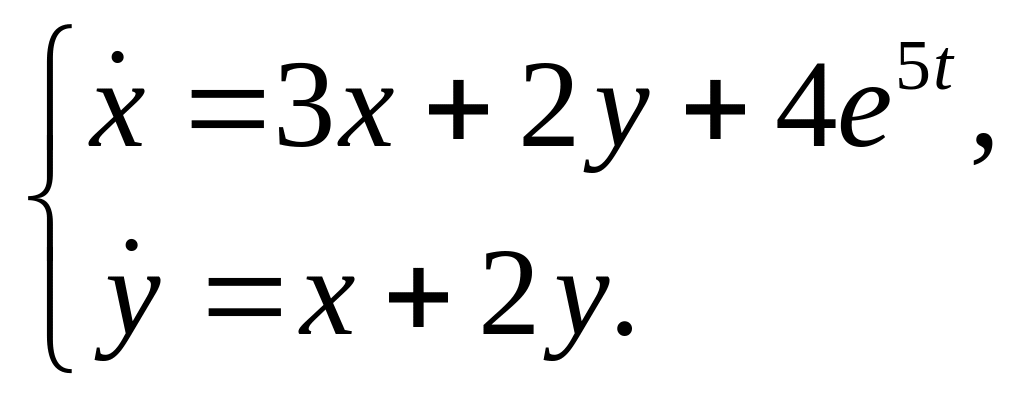
28.
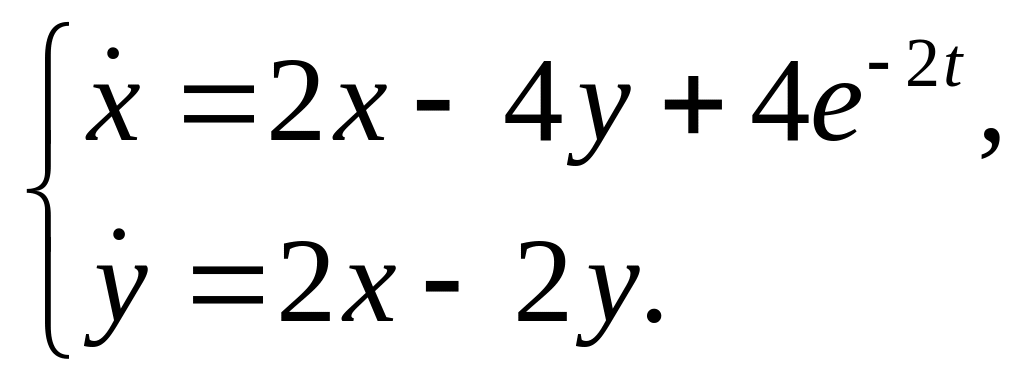 29.
29.
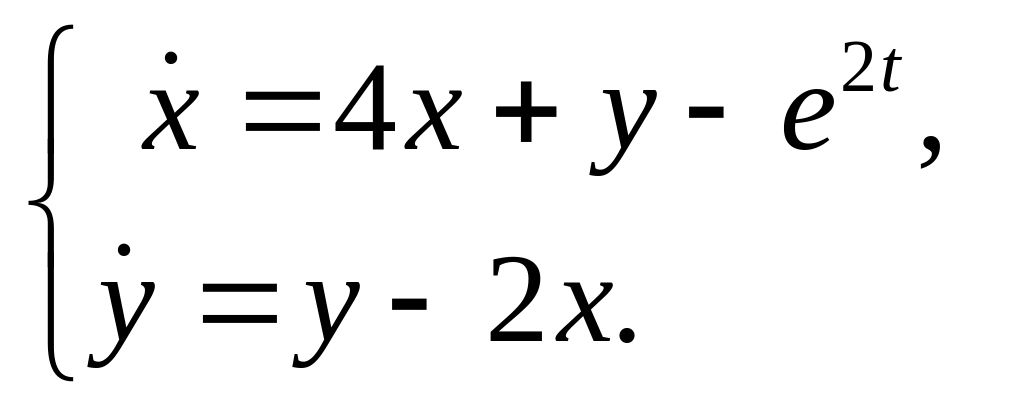
30.
![]() 31.
31.
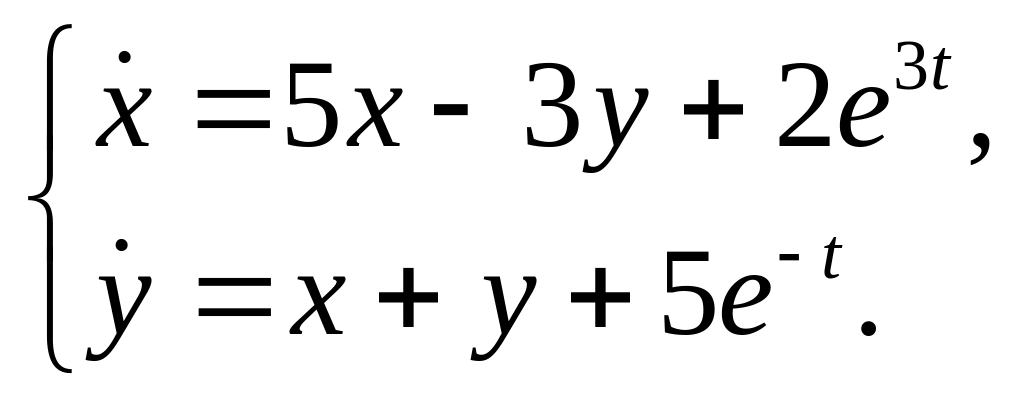 32.
32.
![]()
Ответы: 1.
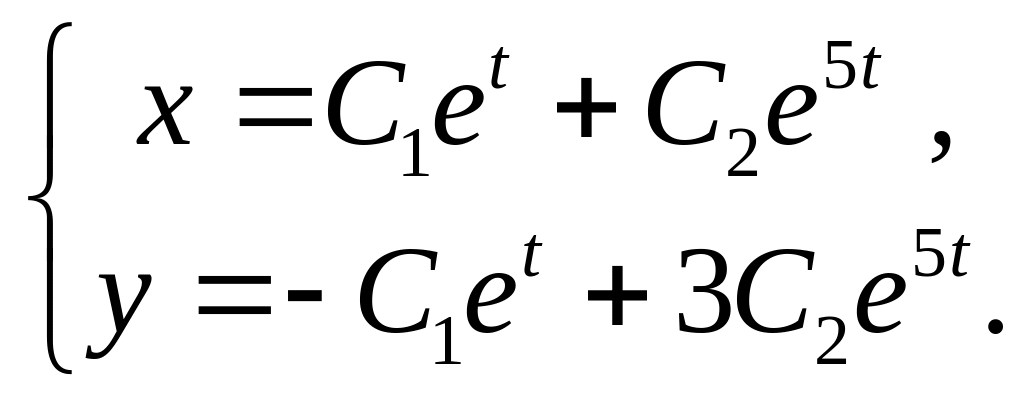 2.
2.
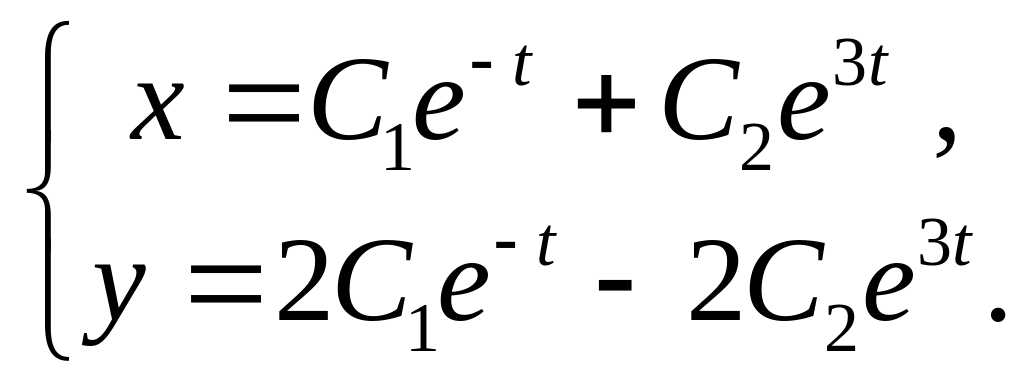
3.
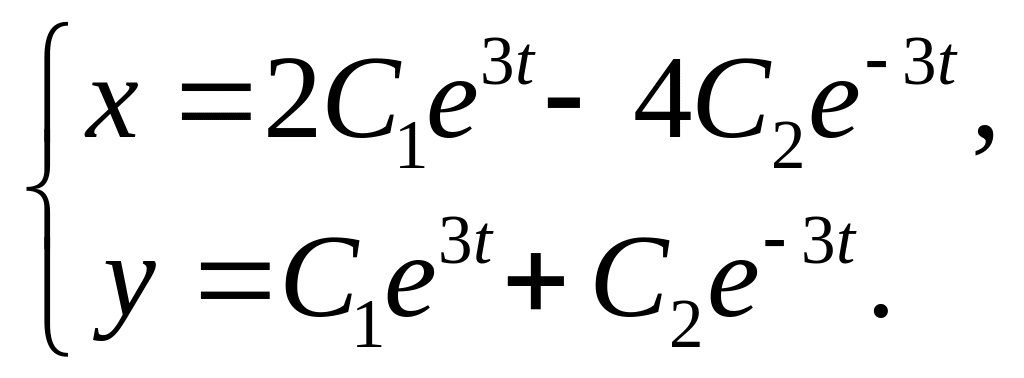 4.
4.
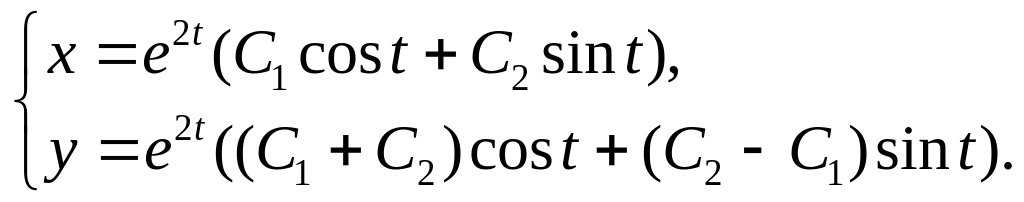
5.
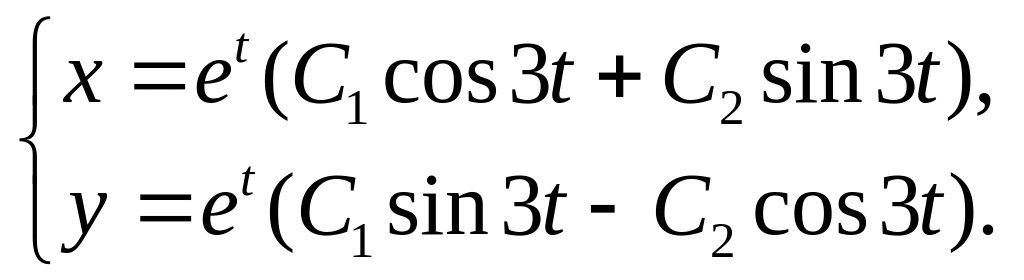
6.
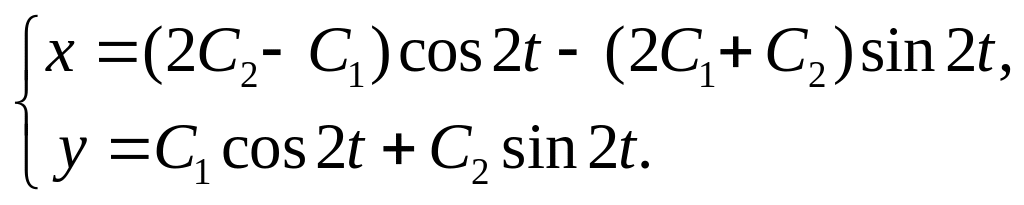 7.
7.
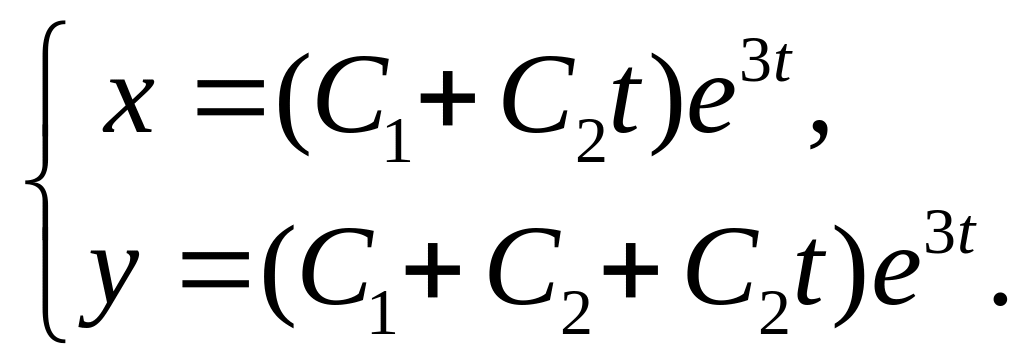
8.
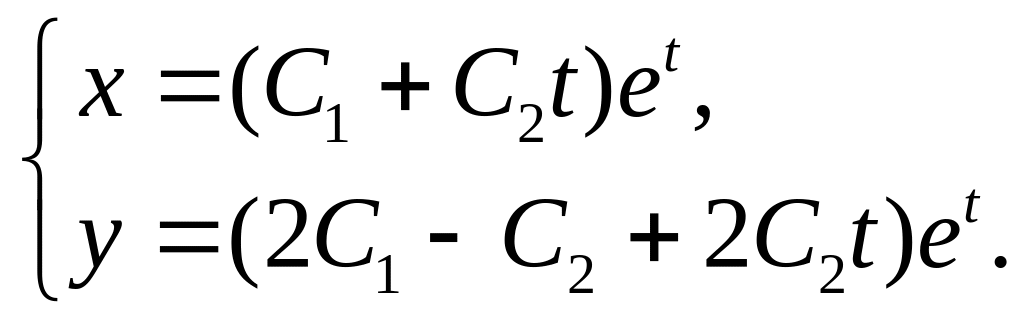 9.
9.
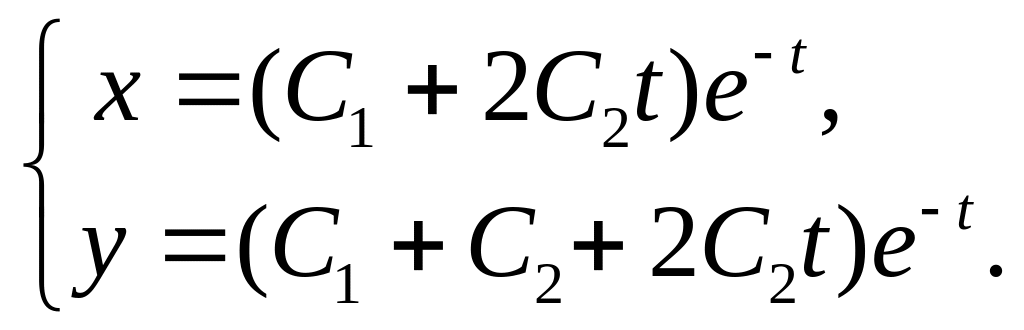
10.
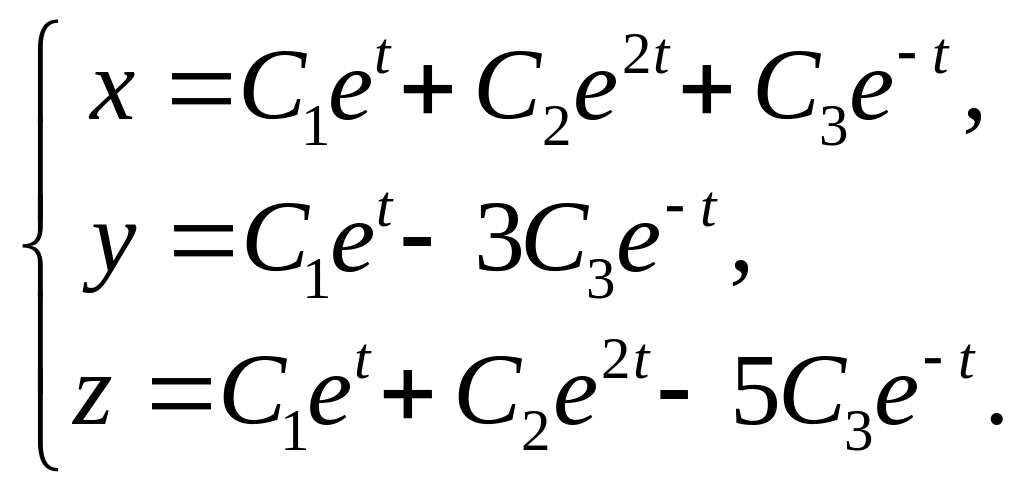 11.
11.
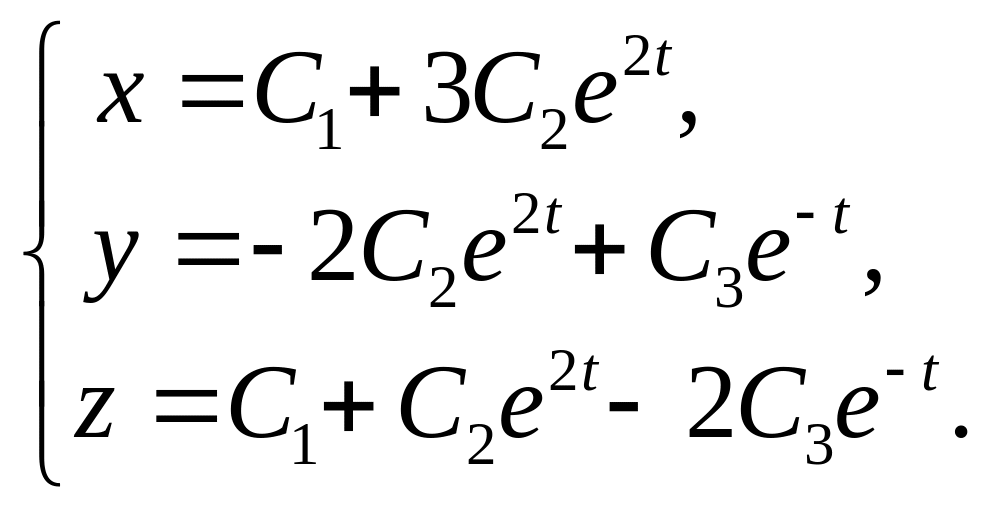
12.
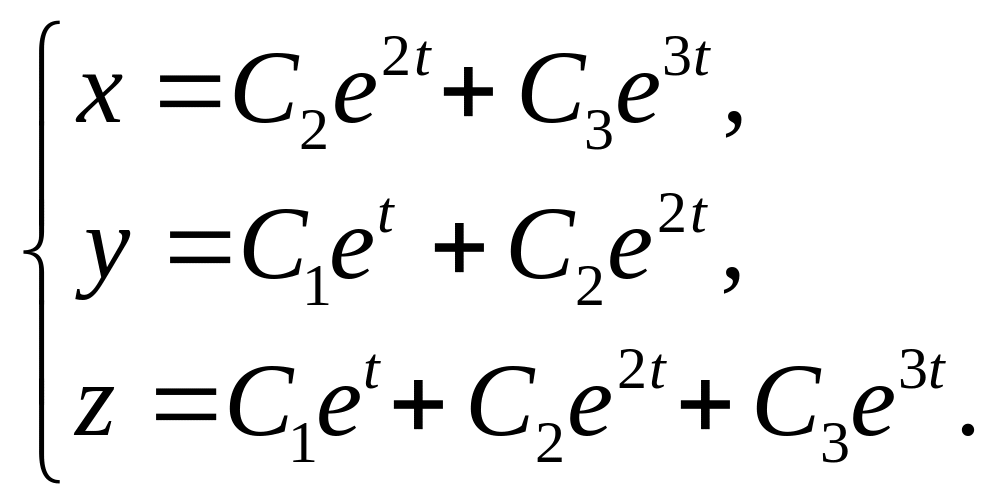 13.
13.
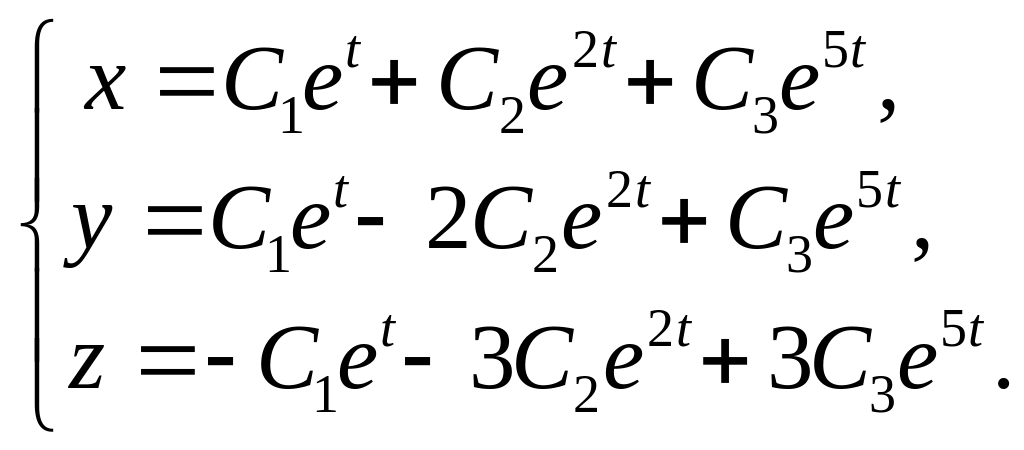
14.
 15.
15.
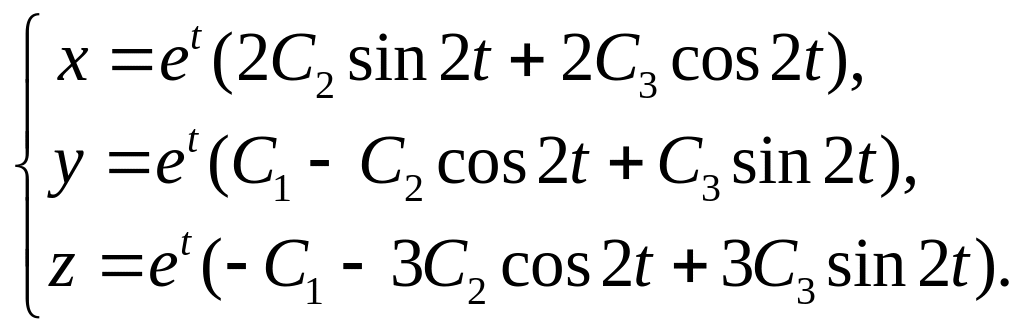
16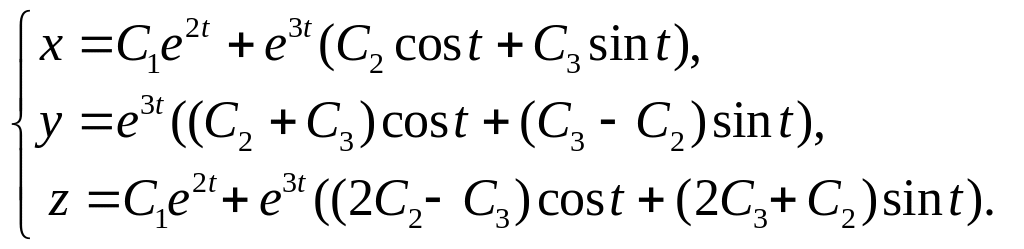
17.

18.
 19.
19.
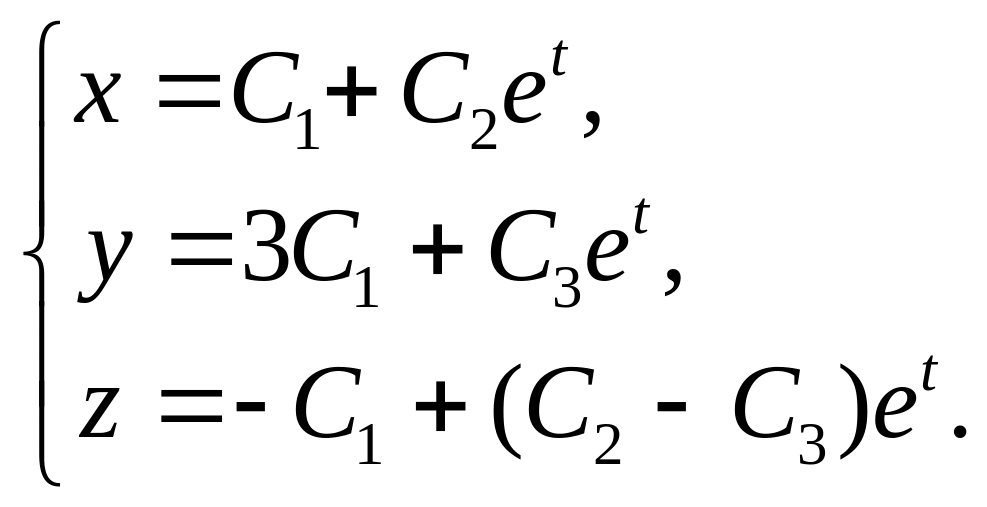
20.
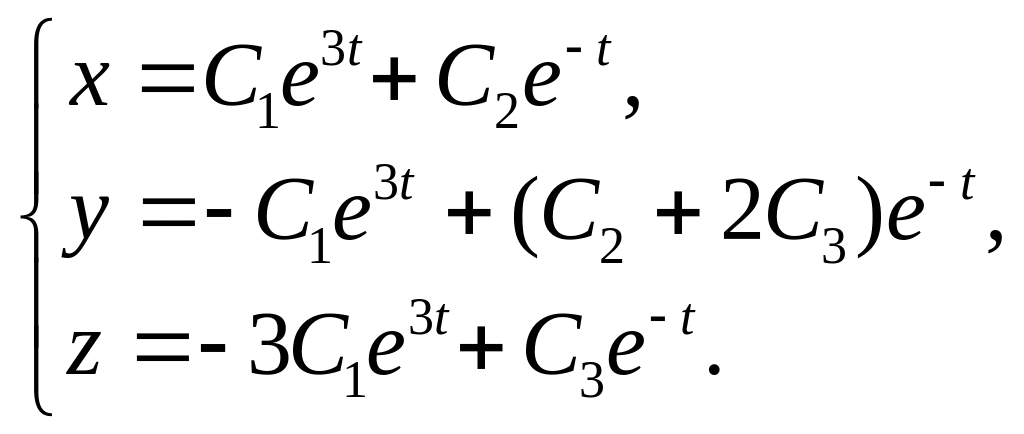 21.
21.
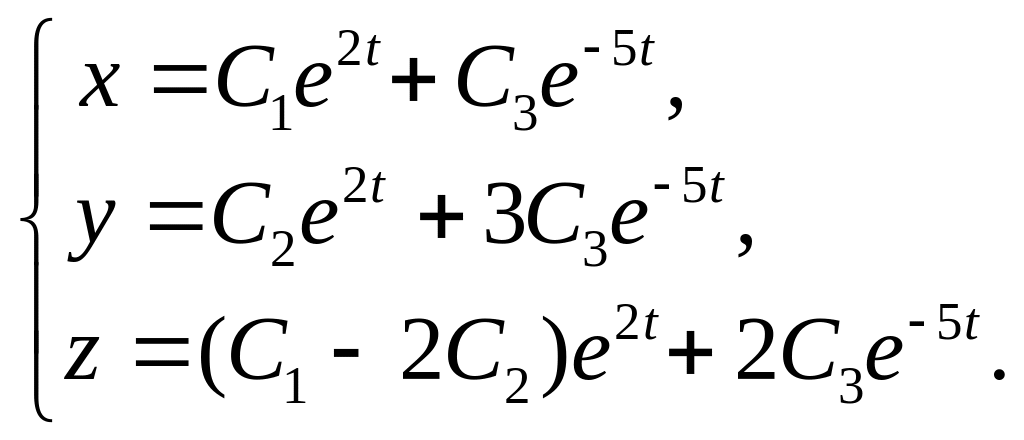
22.
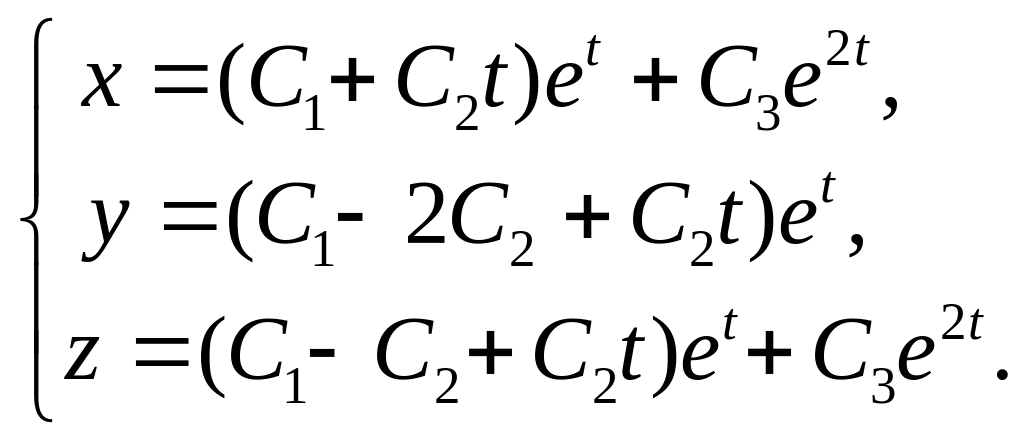 23.
23.
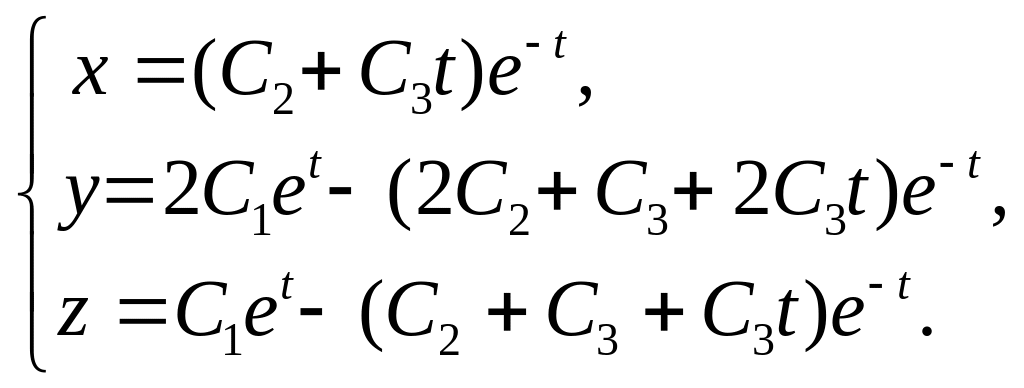
24.
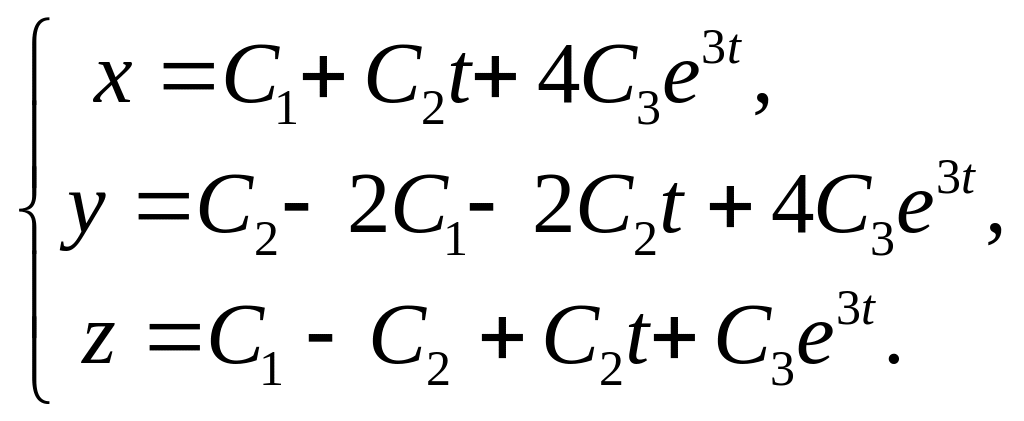
25.
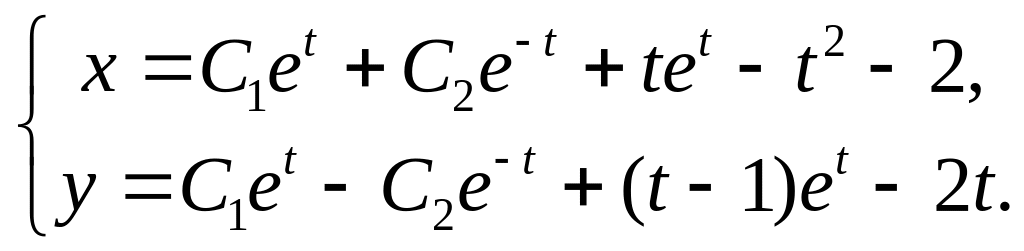 26.
26.
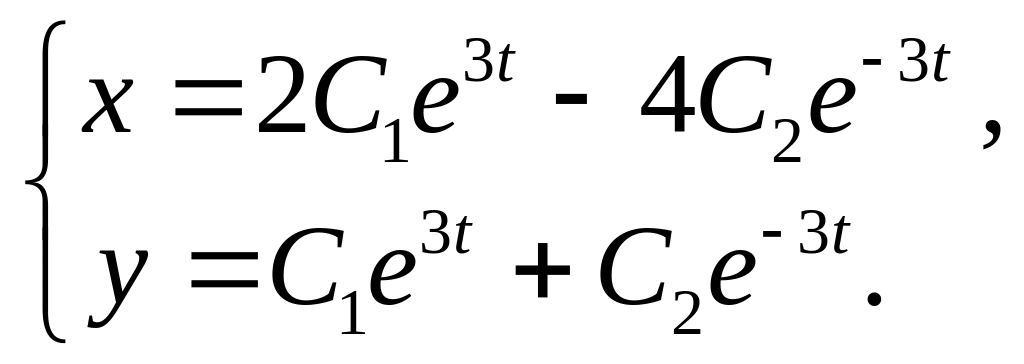
27.
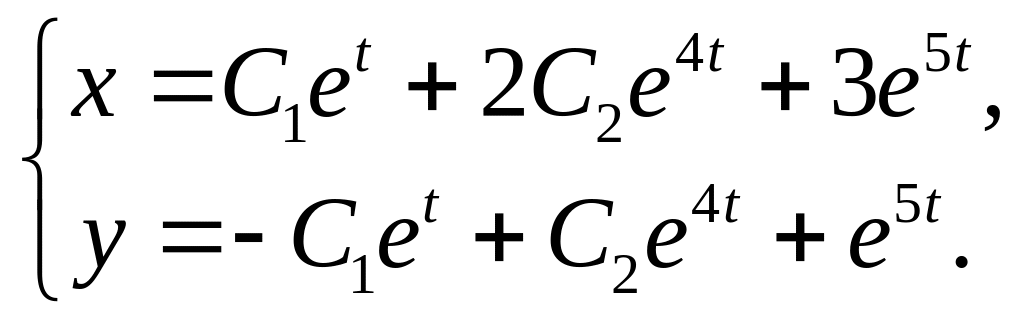
28.
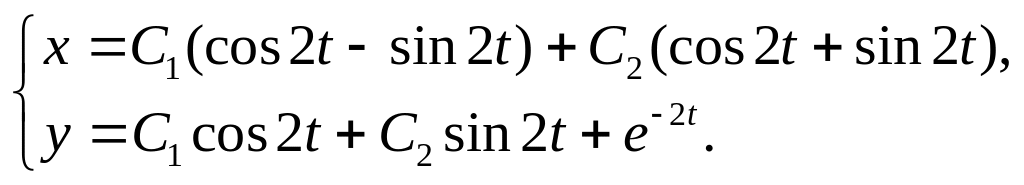
29.
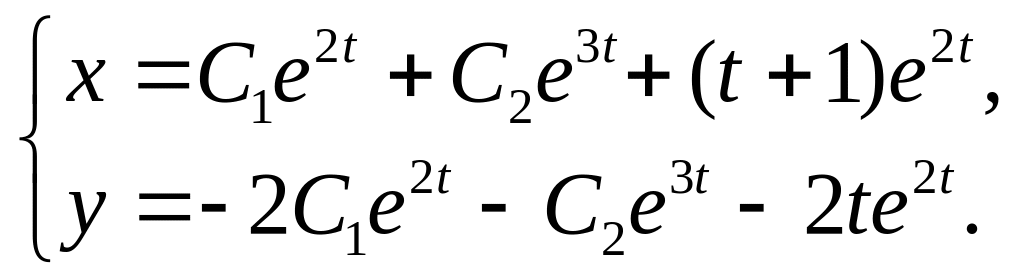 30.
30.
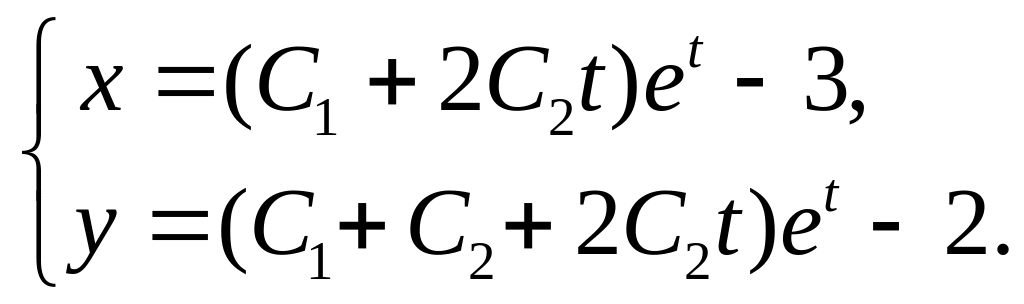
31.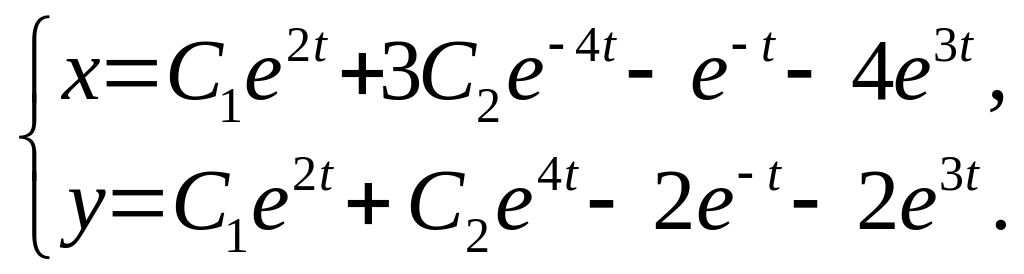 32.
32.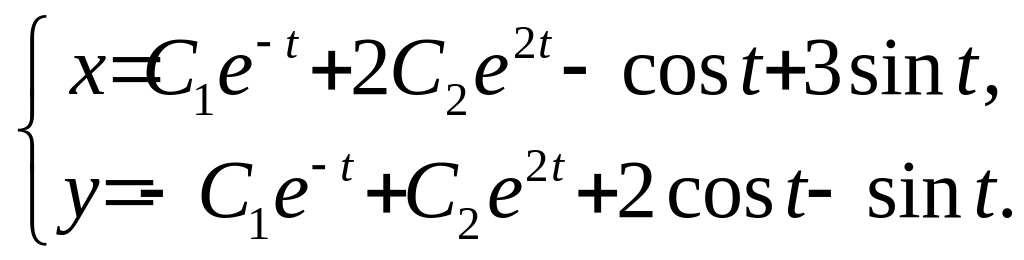
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Пискунов Н.С. Дифференциальные и интегральные исчисления / Н.С. Пискунов.- М.: Наука, 2001.Т.2.- 576 с.
2. Агафонов С.А. Дифференциальные уравнения / С.А. Ага-
фонов, А.Д. Герман, Т.В. Муратова. - М.: Изд-во МГТУ им.
Н.Э. Баумана, 2000.-348 с.
3. Данко П.Е. Высшая математика в упражнениях и задачах / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М.: «Оникс 21
век» «Мир и образование», 2003. Ч. 2.
4. Зимина О.В. Высшая математика / О.В. Зимина, А.И. Кириллов, Т.А. Сальникова.- М.: Физико-математическая литература, 2001.-368 с.
5. Ефимов А.В. Сборник задач по математике для втузов / А.В. Ефимов, Б.П. Демидович; под ред. А.В. Ефимова. - М.: Наука,1986. –Ч.2.-368 с.
6. Лунгу К.Н. Сборник задач по высшей математике. 2 курс/К.Н. Лунгу, В.П. Норин, Д.Т. Письменный, Ю.А. Шевченко; под ред. С.Н. Федина. - М.: Айрис-пресс, 2005.-592 с.
7. Рябушко А.П. Индивидуальные задания по высшей математике: Комплексные числа. Неопределенные и определенные интегралы. Функции нескольких переменных. Обыкновенные дифференциальные уравнения / А. П. Рябушко и др.; под общ. ред. А. П. Рябушко.- 3-е изд.- Минск.: Выш. шк., 2007.-396 с.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
для организации самостоятельной работы
по изучению раздела «Дифференциальные уравнения» курса «Математика»
для студентов направления подготовки бакалавров 230400 «Информационные системы и технологии».
очной формы обучения
Составители:
Глушко Елена Георгиевна
Дубровская Алевтина Петровна
Провоторова Елена Николаевна
В авторской редакции
ГОУВПО «Воронежский государственный
технический университет»
