4.2. Система линейных дифференциальных уравнений с постоянными коэффициентами.

ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ СИСТЕМЫ

Пусть дана система линейных дифференциальных уравнений с неизвестными функциями, коэффициенты которой постоянные:

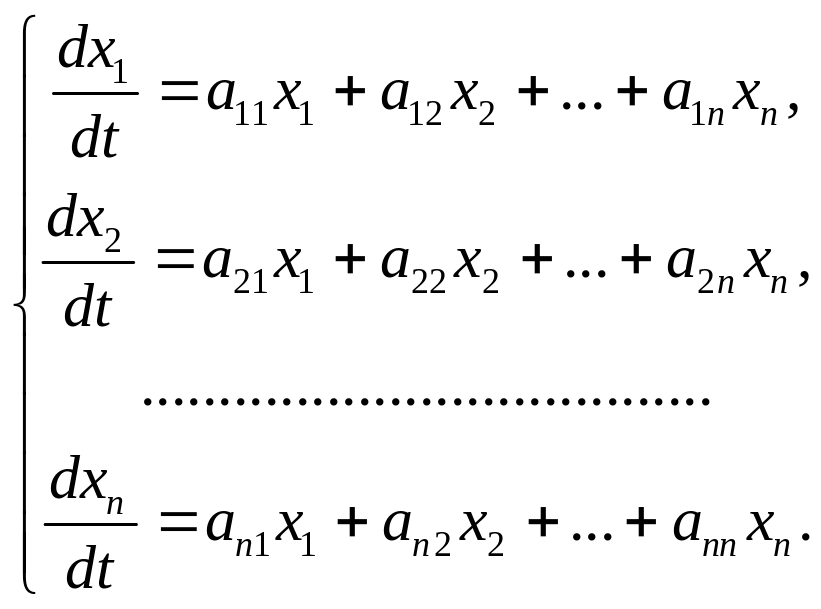
Эту систему можно записать в виде одного матричного дифференциального уравнения

Здесь , , .

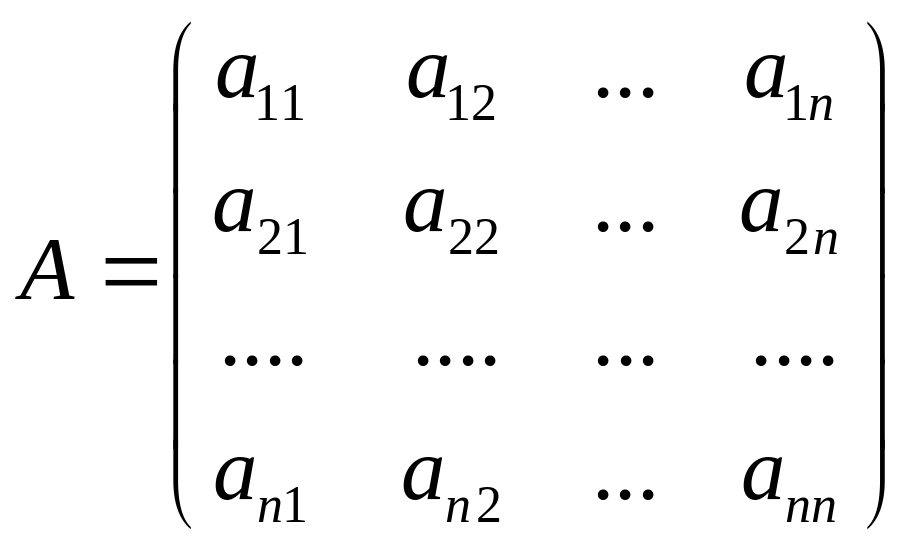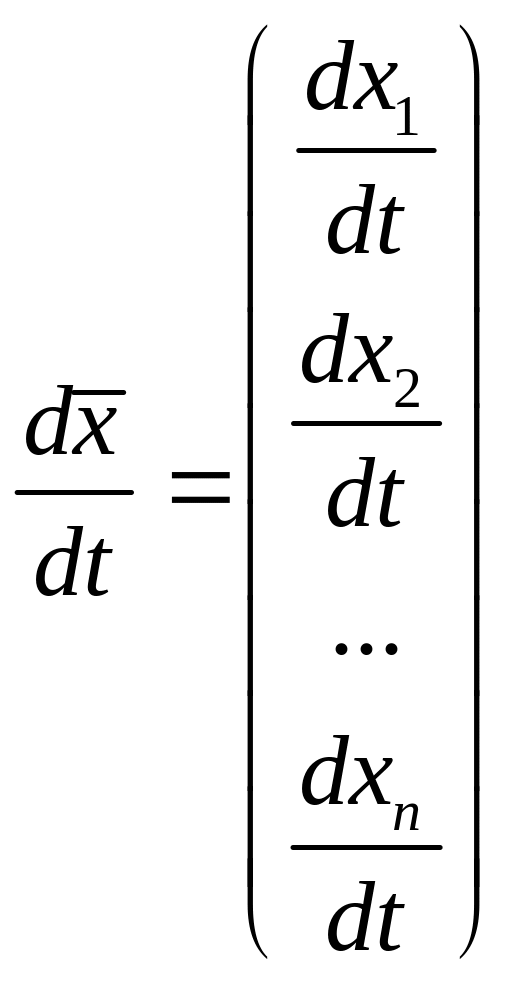Ищем решение системы в виде

Подставив значения в систему дифференциальных уравнений, получим однородную систему линейных алгебраических уравнений относительно

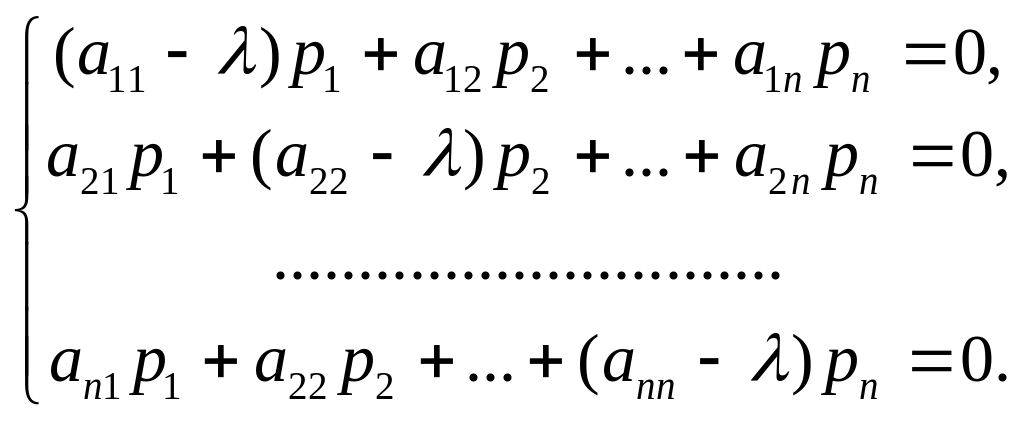
Система должна иметь ненулевое решение, поэтому ее определитель должен быть равен нулю. Для определения получаем уравнение -й степени

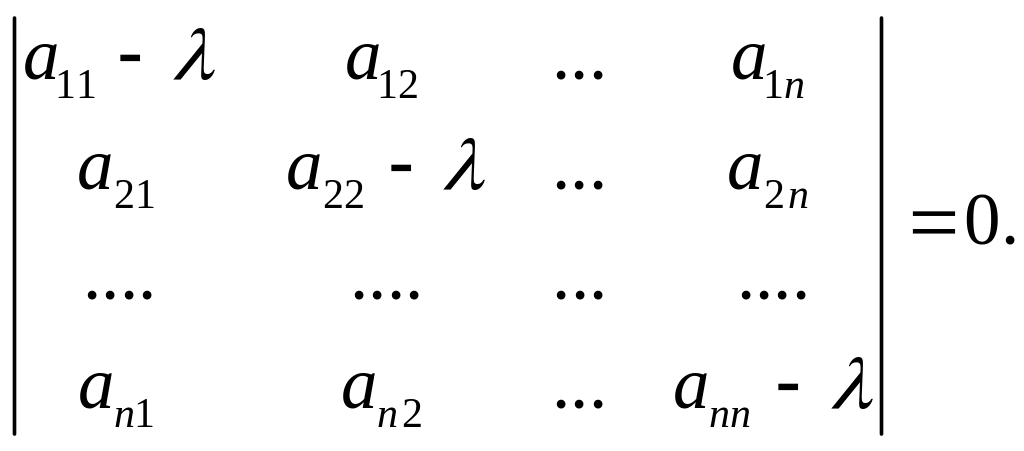
Последнее уравнение является характеристическим уравнением матрицы и в то же время характеристическим уравнением системы.

Предположим, что характеристическое уравнение имеет различных корней , которые являются характеристическими числами матрицы Каждому характеристическому числу соответствует свой собственный вектор. Пусть характеристическому числу соответствует собственный вектор Тогда система дифференциальных уравнений имеет решений: , образующих фундаментальную систему решений. Общее решение однородной системы представляет собой линейную комбинацию фундаментальной системы решений. Тогда общее решение системы имеет вид

Если среди корней характеристического уравнения есть комплексно-сопряженные корни кратности 1, то в фундаментальной системе решений им будут соответствовать , где - собственный вектор, соответствующий

Если - корень кратности , то соответствующее этому корню решение системы ищется в виде вектора

,

координаты векторов определяются из системы линейных уравнений, получающейся приравниванием коэффи -циентов при одинаковых степенях .

Пример 4.3. Найти общее решение системы ОДУ

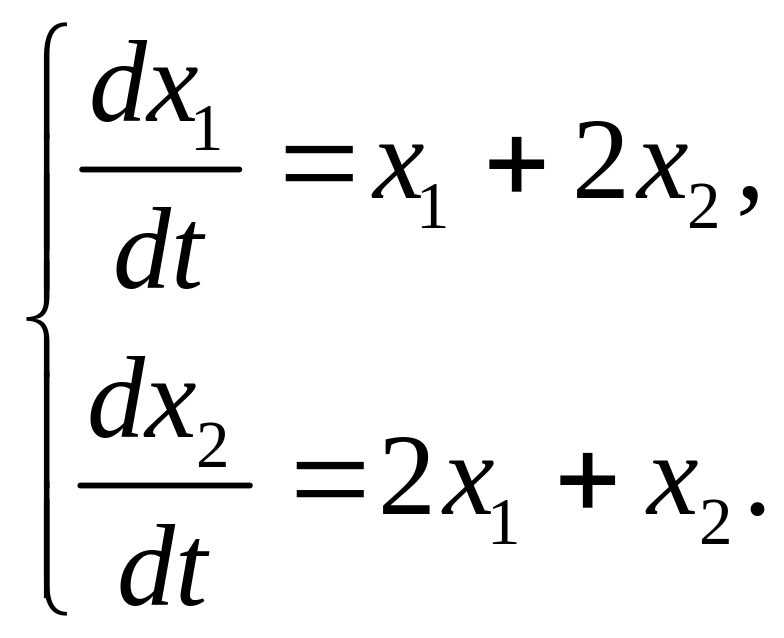
Решение. Матрица и характеристическое уравнение системы в данном случае имеют вид

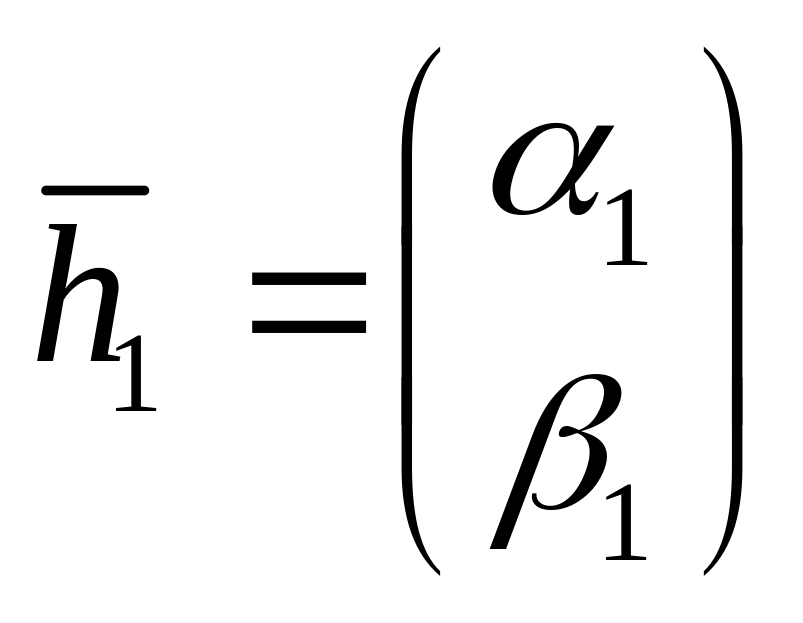Раскрывая определитель, получаем квадратное уравнение , имеющее два действительных различных корня Они являются собственными значениями матрицы Найдем собственные векторы матрицы , отвечающие этим собственным значениям. Пусть соответствует собственный вектор , тогда ,

или 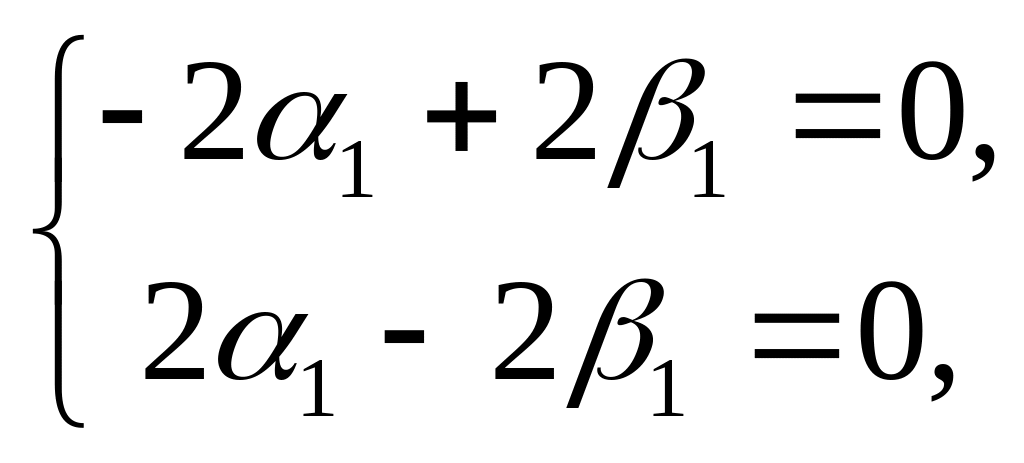одно из решений , т.е. значе-

нию соответствует собственный вектор .

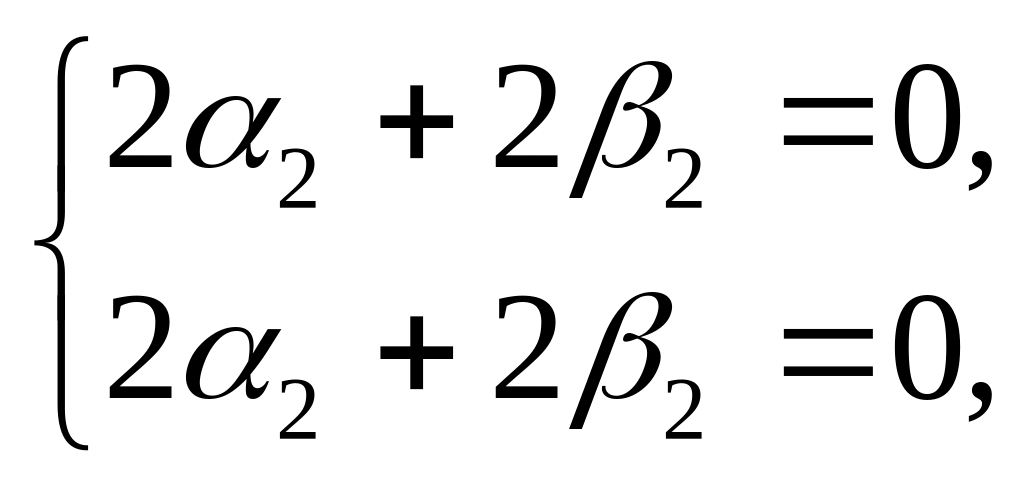
При собственный вектор находим из системы , или , одно из решений , т.е. собственному значению соответствует собственный вектор . Таким образом, вектор-функции образуют фундаментальную систему решений рассматриваемой системы ОДУ. Тогда общее решение этой системы в векторной форме имеет вид

или в координатной форме

Пример 4.4. Найти общее решение системы ОДУ

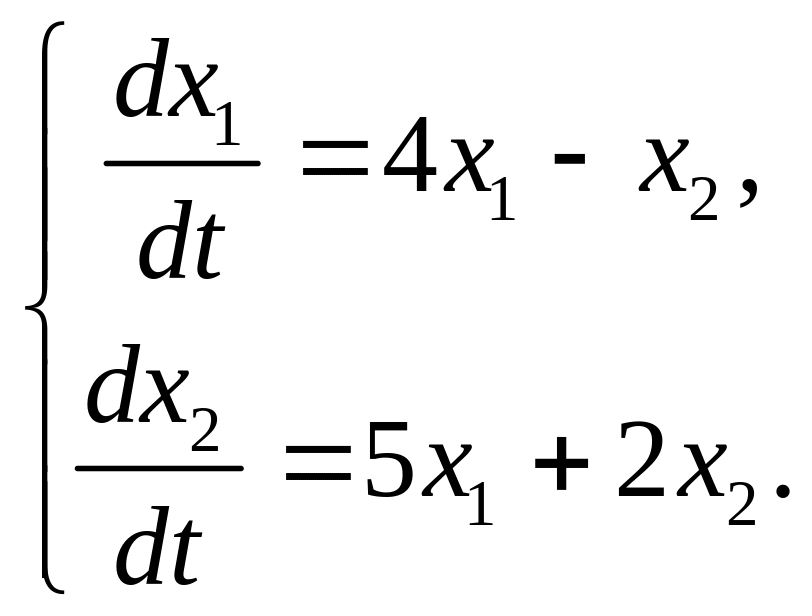
Решение. Матрица и характеристическое уравнение системы в данном случае имеют вид

Раскрывая определитель, получаем квадратное уравнение , имеющее два комплексно-сопряженных корня Корню соответствует собственный

вектор , тогда , и функции

образуют фундаментальную систему решений для рассматриваемой системы ОДУ. Общее решение этой системы можно представить в виде

,

Решение системы в координатной форме:

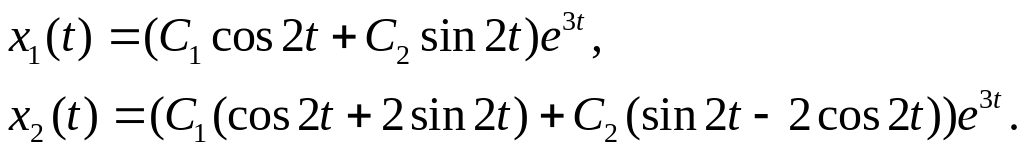
Пример 4.5. Найти общее решение системы ОДУ

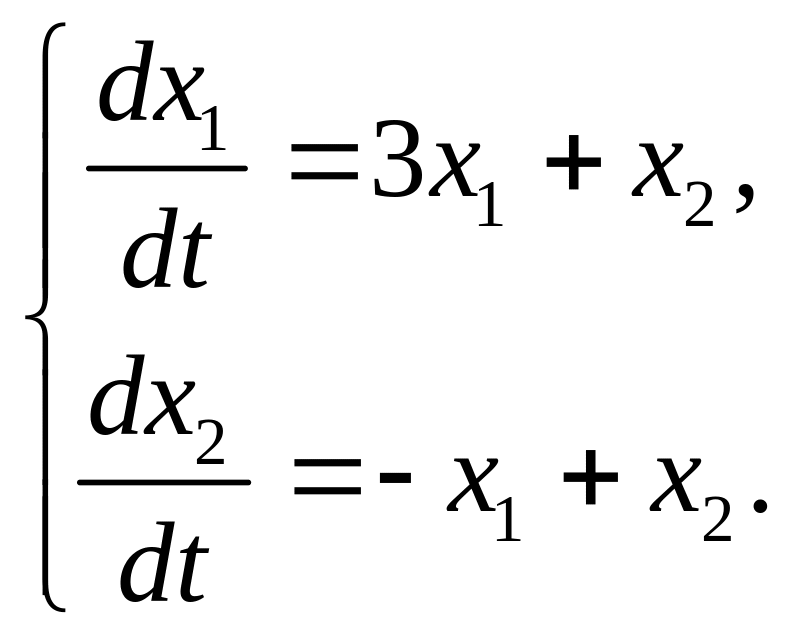
Решение. Матрица и характеристическое уравнение системы в данном случае имеют вид

Характеристическое уравнение системы имеет один корень кратности, равной двум. Ранг матрицы СЛАУ , соответствующей этому корню, равен едини-

це. Решение будем искать в виде

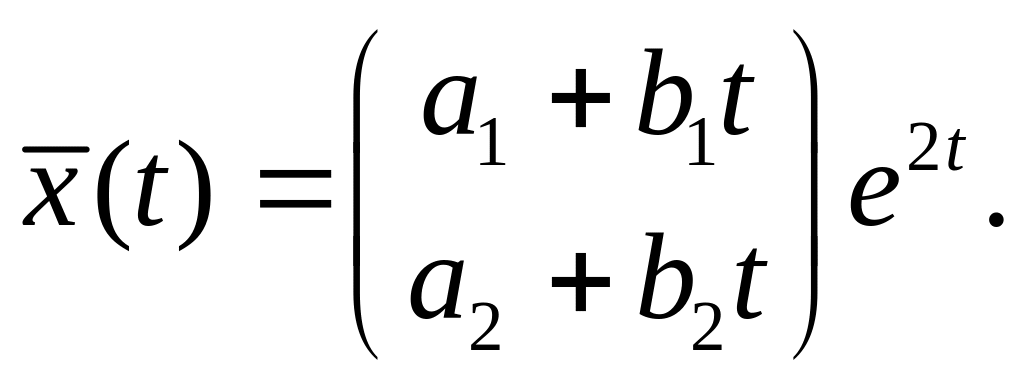
Подставим это выражение в систему ОДУ, сократим на и в результате получим

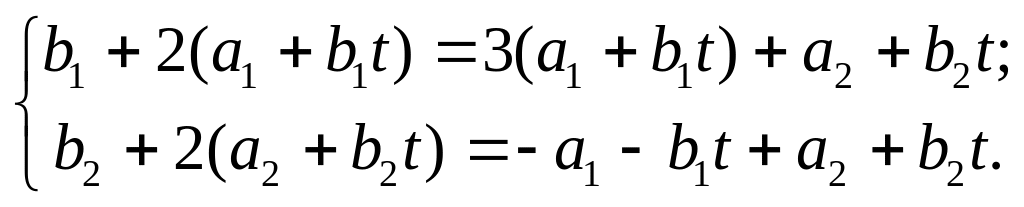
Приравняв коэффициенты при одинаковых степенях , получим однородную систему четырех линейных уравнений с четырьмя неизвестными , имеющую два линейно независимых решения. Решению СЛАУ соответствует решение системы ОДУ. Взяв в качестве второго решения СЛАУ , получим второе решение системы ОДУ: . Общим решением системы ОДУ будет

.