- •Часть 2
- •§3. Линейные дифференциальные уравнения
- •3.1. Линейно независимые функции
- •3.2. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •3.3. Линейные неоднородные дифференциальные уравнения (лнду) второго порядка
- •§ 4. Системы дифференциальных уравнений
- •4.1. Нормальные системы дифференциальных уравнений
- •4.2. Система линейных дифференциальных уравнений с постоянными коэффициентами.
- •4.3 Линейные неоднородные системы
- •394026 Воронеж,
§ 4. Системы дифференциальных уравнений
Системой дифференциальных уравнений называется совокупность дифференциальных уравнений, каждое из которых содержит независимую переменную, искомые функции и их производные.
4.1. Нормальные системы дифференциальных уравнений
Система дифференциальных уравнений первого порядка, разрешенных относительно производной, т.е. система вида
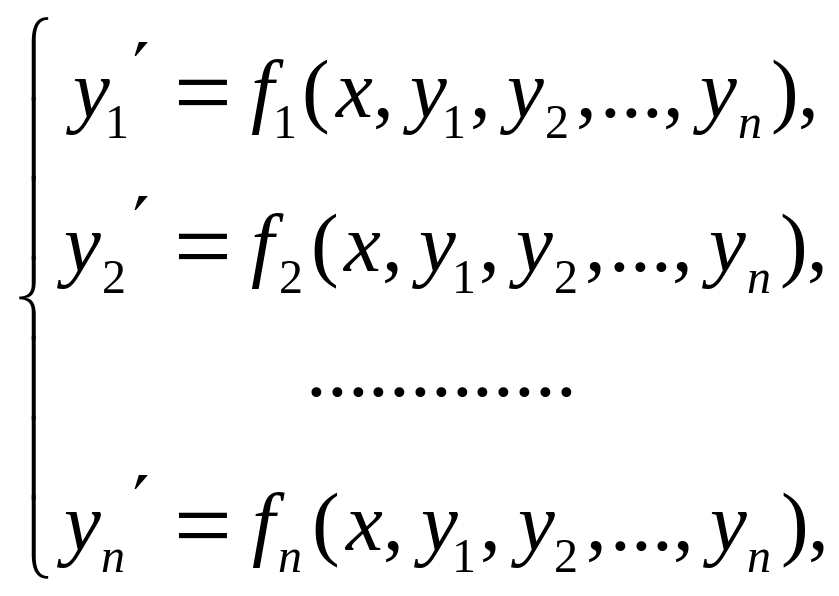 (4.1)
(4.1)
где
-
независимая переменная, а
![]() -
неизвестные функции от
,
называется нормальной системой.
-
неизвестные функции от
,
называется нормальной системой.
Решить эту систему означает найти функции
,
удовлетворяющие системе (4.1) .
Нормальную систему можно привести
к одному уравнению порядка
(или меньше) относительно одной неизвестной
функции, скажем
![]() при помощи следующего алгоритма,
называемого методом исключения.
при помощи следующего алгоритма,
называемого методом исключения.
Дифференцируем первое уравнение
системы по переменной
:
![]() .
.
Производные
![]() в правой части этого равенства заменим
их выражениями из системы (4.1). Получим
уравнение
в правой части этого равенства заменим
их выражениями из системы (4.1). Получим
уравнение
![]() .
Это равенство снова дифференцируем по
переменной
:
.
Это равенство снова дифференцируем по
переменной
:
![]() .
.
Производные
в правой части этого равенства заменим
их выражениями, заданными системой
(4.1). Получим еще одно уравнение
![]() .
Это уравнение
.
Это уравнение
дифференцируем по переменной
и так далее до тех пор, пока не придем к
уравнению
![]() .
.
Полученные таким образом дифференциальные уравнения объединим в одну систему, к которой присоединим первое уравнение системы (4.1)
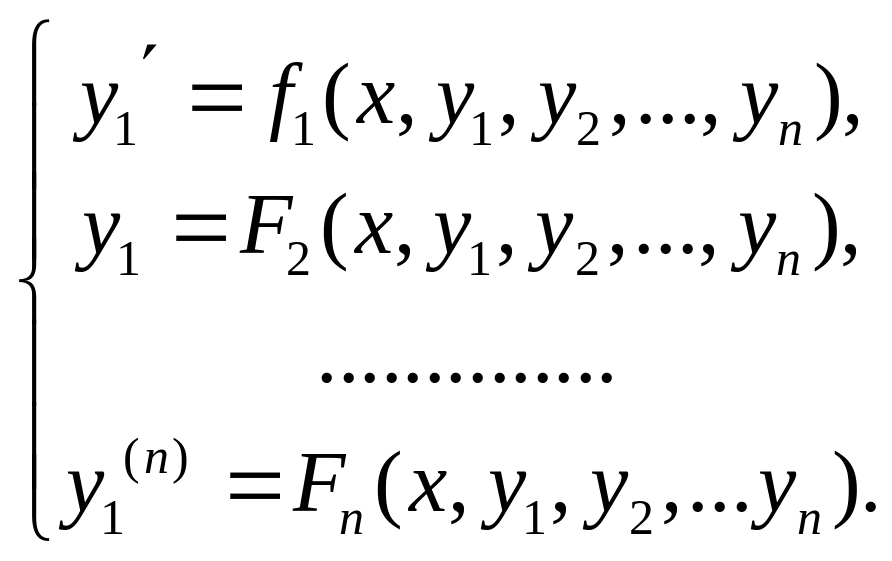 (4.2)
(4.2)
Первые
![]() уравнений системы (4.2) разрешим относительно
уравнений системы (4.2) разрешим относительно
переменных
![]() ,
выражая их через переменные
и
,
выражая их через переменные
и
![]() ,
а также производные
,
а также производные
![]() .
Полученные выражения подставим в
последнее уравнение системы (4.2). В итоге
придем к дифференциальному уравнению
порядка
относительно неизвестной функции
.
.
Полученные выражения подставим в
последнее уравнение системы (4.2). В итоге
придем к дифференциальному уравнению
порядка
относительно неизвестной функции
.
Из общего решения этого уравнения можно получить общее решение системы (4.1) или требуемое частное решение. Заметим, что порядок последнего уравнения может быть меньше, чем , если при его получении были использованы не все уравнения системы (4.1).
Пример 4.1. Решить систему дифференциальных уравнений:
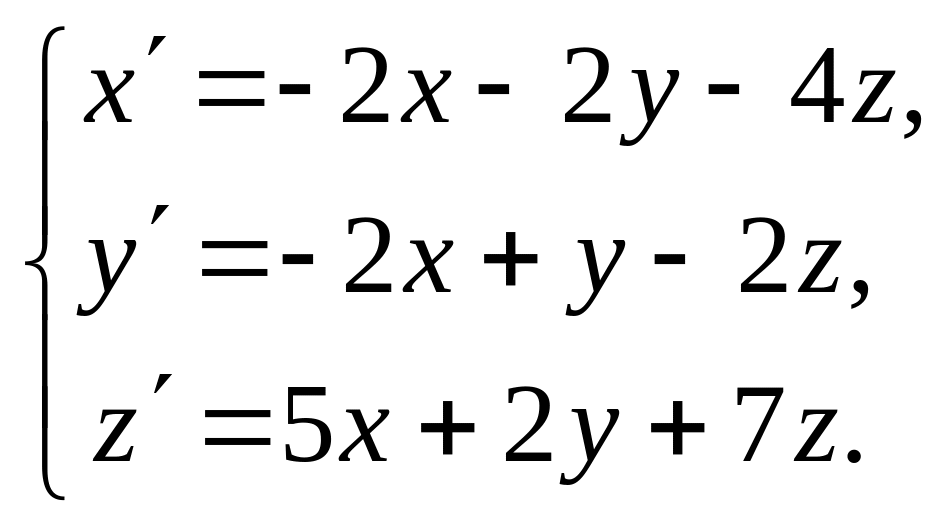
Решение. В данной системе
![]()
![]() -
неизвестные функции, а независимая
переменная
-
неизвестные функции, а независимая
переменная
![]() -
их аргумент.
-
их аргумент.
Дифференцируем первое уравнение системы по :
![]() .
.
Вместо
![]() и
и
![]() подставим их выражения из второго и
третьего уравнений системы. Получаем
подставим их выражения из второго и
третьего уравнений системы. Получаем
![]() ,
,
откуда
![]()
Полученное уравнение дифференцируем
по
,
а вместо
и
опять
подставим выражения из тех же уравнений
системы
![]()
Составим новую систему:
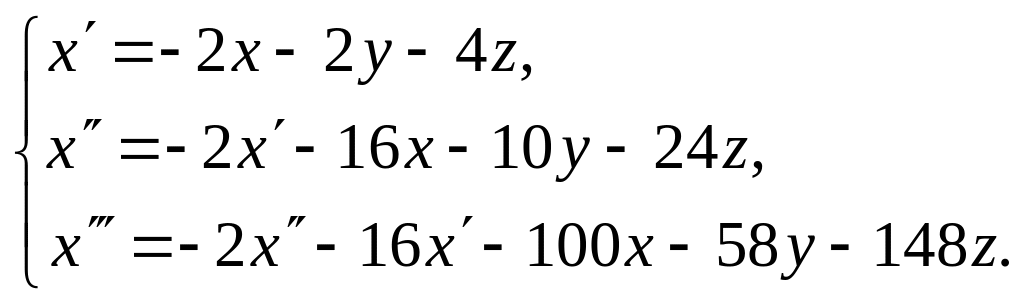
Система состоит из первого уравнения исходной системы и двух уравнений, полученных последовательным дифференцированием.
Из этой системы исключим неизвестные
и
![]() .
Для этого проще всего использовать
первые два уравнения системы, из которых,
после преобразования (рассматривая
.
Для этого проще всего использовать
первые два уравнения системы, из которых,
после преобразования (рассматривая
![]() и
и
![]() ,
находим
,
находим
![]()
И эти выражения подставим в третье уравнение системы:
![]()
После приведения подобных слагаемых
получаем одно уравнение третьего порядка
(однородное с постоянными коэффициентами)
относительно неизвестной функции
![]() :
:
![]()
Корнями его характеристического уравнения
![]() являются числа
являются числа
![]() Следовательно, общее решение последнего
уравнения имеет вид
Следовательно, общее решение последнего
уравнения имеет вид
![]()
Теперь надо получить значение для
и
![]() .
Это легко сделать, имея в виду систему,
содержащую
.
Это легко сделать, имея в виду систему,
содержащую
![]() и
и
![]() ,
выраженные через
,
выраженные через
![]() .
Поэтому сначала находим
.
Поэтому сначала находим
![]() .
.
Остается сделать соответствующие подстановки:
![]()
![]()
Аналогично,
![]() Окончательно, получаем
Окончательно, получаем
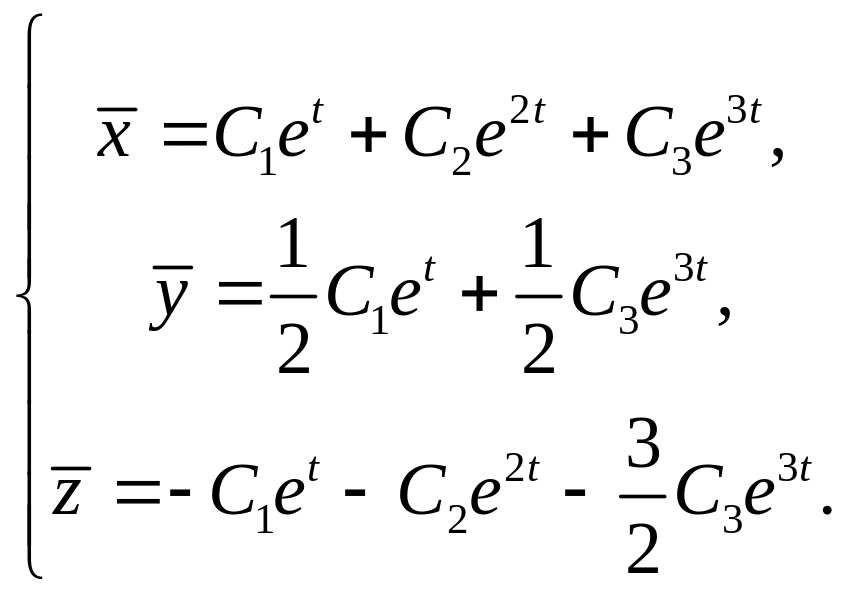
Пример 4.2. Решить систему
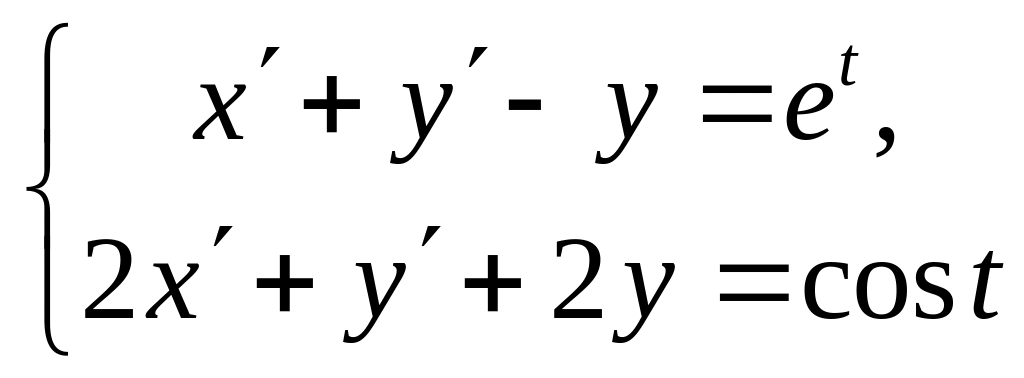 при заданных начальных условиях
при заданных начальных условиях
![]()
Решение. Сначала приводим систему к нормальному виду, т.е. к виду, разрешенному относительно производных

Далее действуем по схеме, примененной при решении предыдущего примера.
Первое уравнение дифференцируем по , после чего вместо подставим выражение из второго уравнения новой системы
![]() т.е.
т.е.
![]()
из которого исключим , для этого первое уравнение, умноженное на (-4) прибавим ко второму:
![]()
Полученное неоднородное уравнение
второго порядка с постоянными
коэффициентами решается стандартным
способом подбора частного решения.
Решаем однородное уравнение
![]() .
Для этого составляем характеристическое
уравнение
.
Для этого составляем характеристическое
уравнение
![]() .
Его корни
.
Его корни
![]() - вещественные и различные, поэтому
общее решение однородного уравнения
имеет вид
- вещественные и различные, поэтому
общее решение однородного уравнения
имеет вид
![]() .
Частное решение неоднородного уравнения
будем искать методом неопределенных
коэффициентов в виде
.
Частное решение неоднородного уравнения
будем искать методом неопределенных
коэффициентов в виде
![]()
Находим
![]()
Подставляем
![]() в неоднородное уравнение и приравниваем
коэффициенты при функциях
в неоднородное уравнение и приравниваем
коэффициенты при функциях
![]() в левой и правой частях равенства,
получаем систему для нахождения
коэффициентов
в левой и правой частях равенства,
получаем систему для нахождения
коэффициентов
![]()
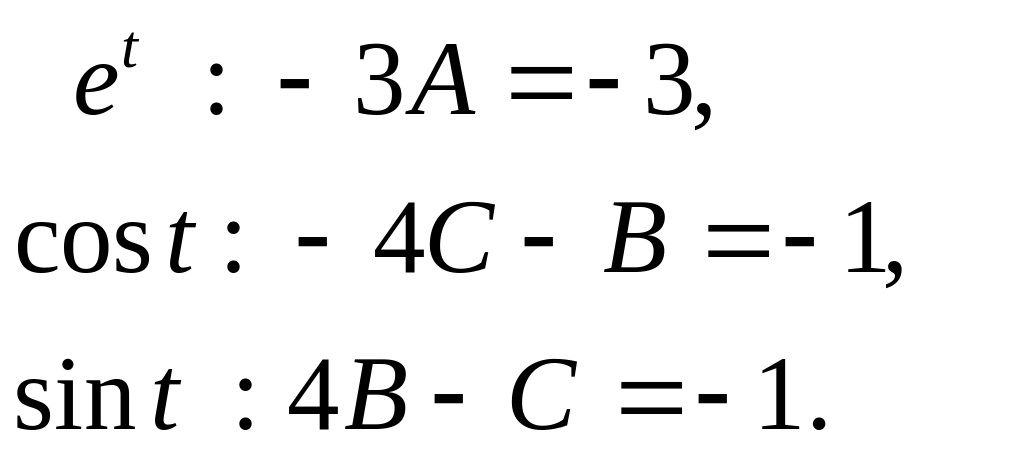
Следовательно
![]() ,
отсюда
,
отсюда
![]()
Окончательно получаем общее решение
неоднородного уравнения
![]()
Другую функцию можно найти двумя способами.
а) Из второго уравнения системы находим
![]()
Подставляя сюда найденное выражение
для
![]() ,
находим
.
,
находим
.
б) Из первого уравнения нормальной системы имеем
![]()
Отсюда, учитывая, что
![]() ,
получим
,
получим
![]()
Таким образом, общее решение системы имеет вид
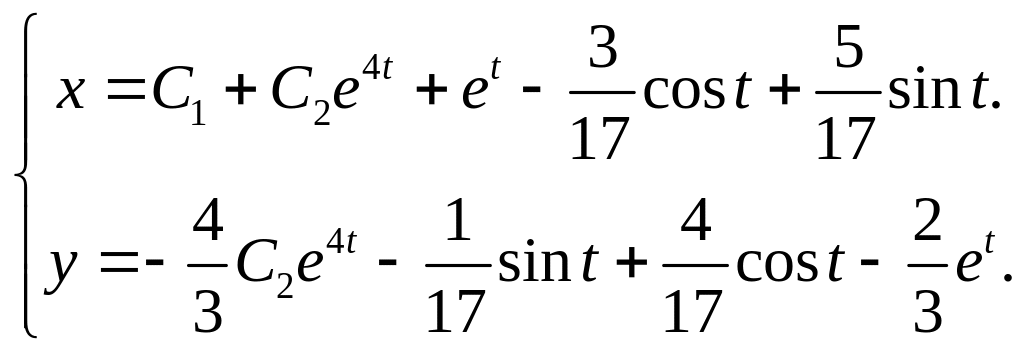
Подставляя начальные условия
![]() ,
определяем константы
и
,
определяем константы
и
![]()
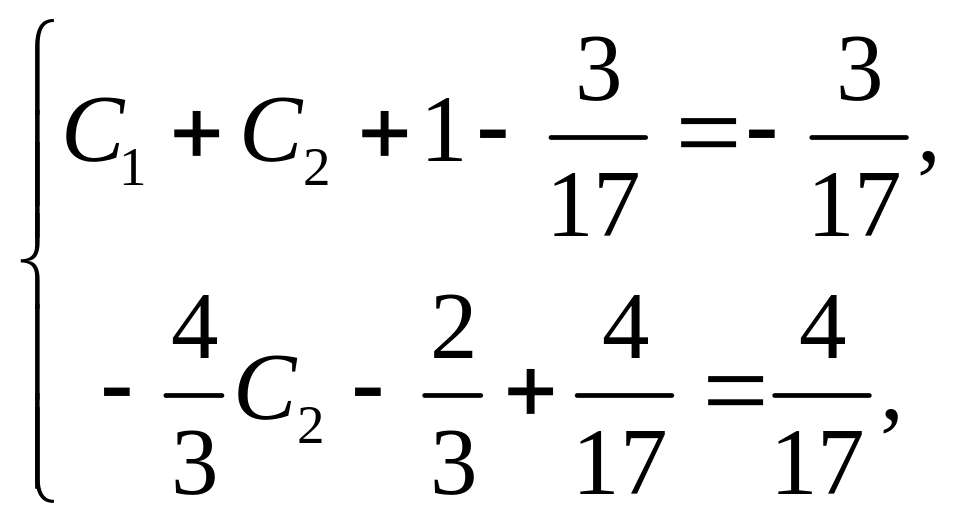 следовательно,
следовательно,
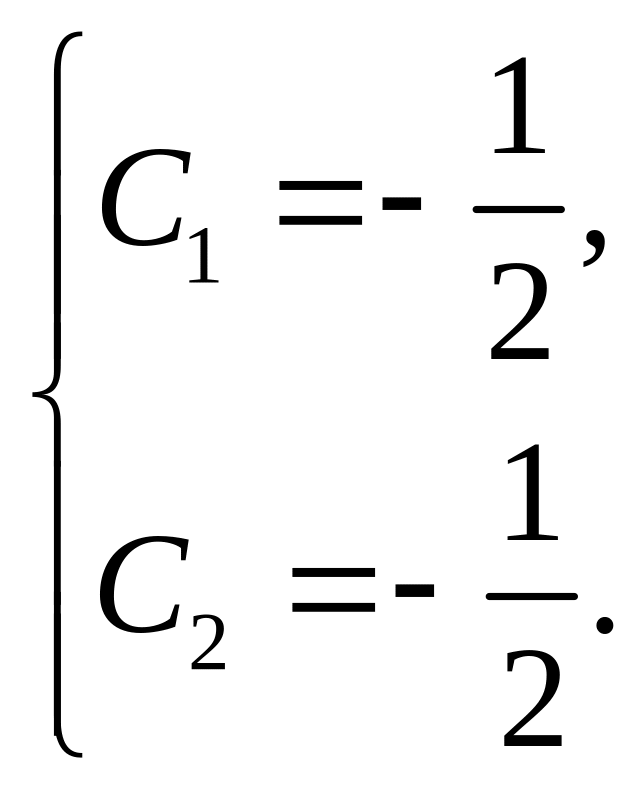
Итак, частные решения, удовлетворяющие начальным условиям, имеют вид

Решить данные системы дифференциальных уравнений:
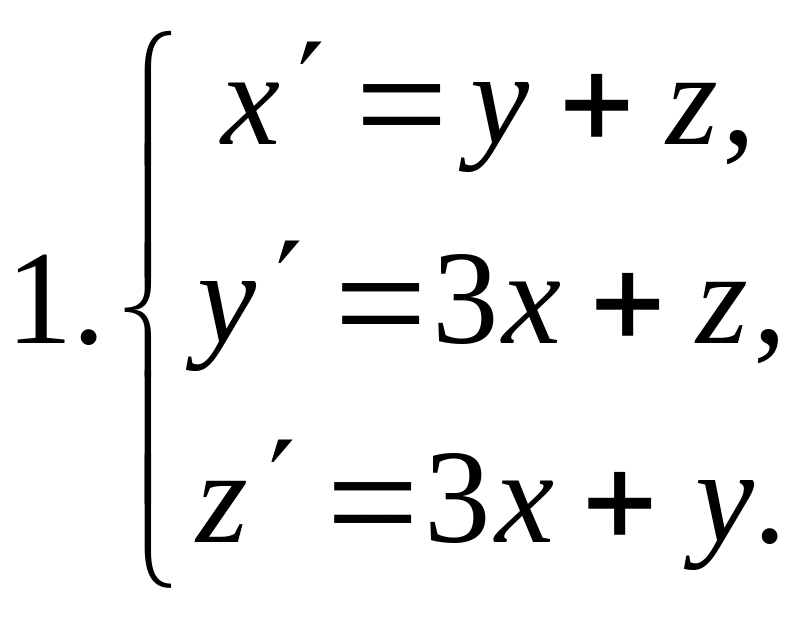 2.
2.![]()
3.
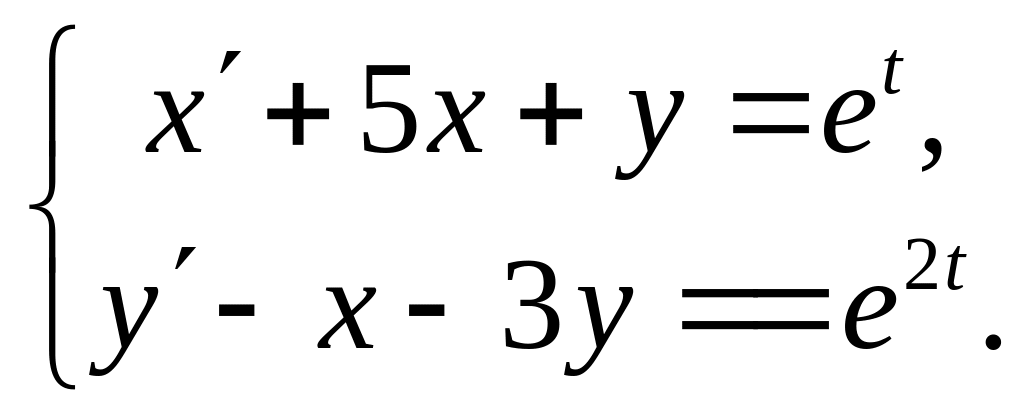 4.
4.
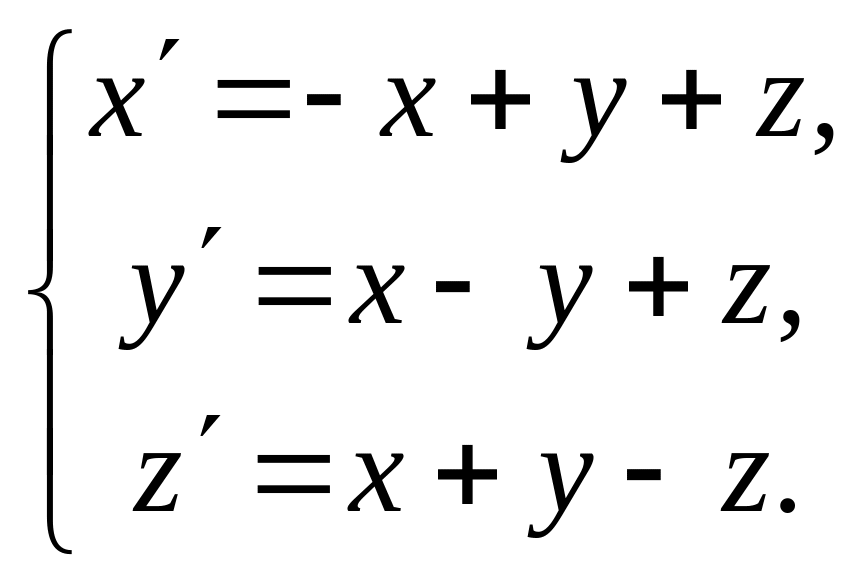 5.
5.![]()
6.
![]() 7.
7.
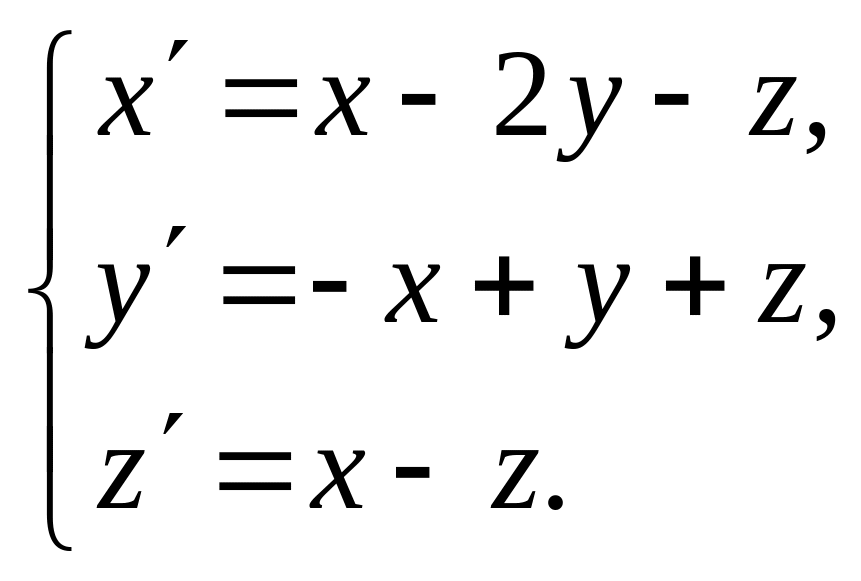 8.
8.
![]()
Ответы:
1.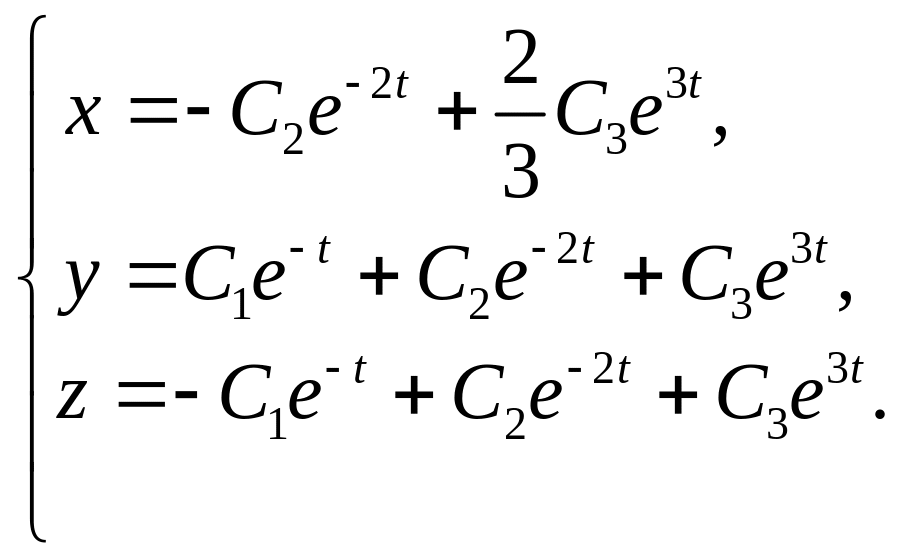 2.
2.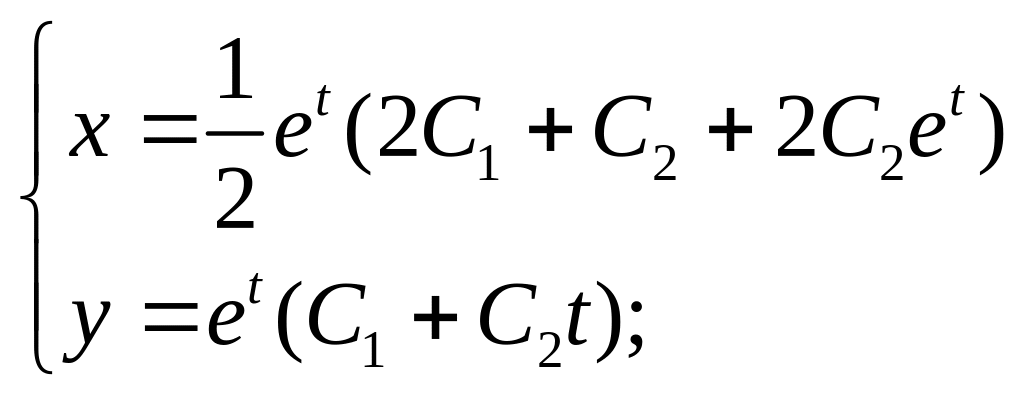
3.ь данные системы дифференциальных уравнений:
енияффициентов в виде
ентами решается стандартным
способом подбора частно
3.
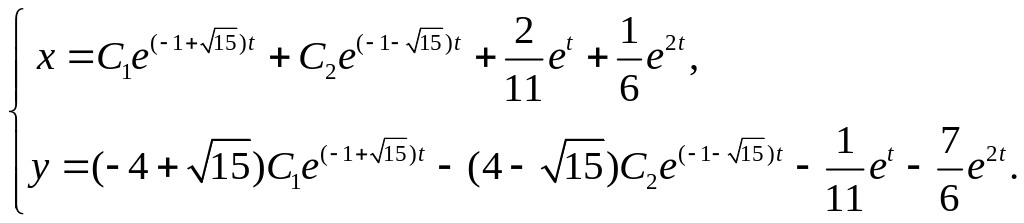
4. уравнение Е СИСТЕМЫ
ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ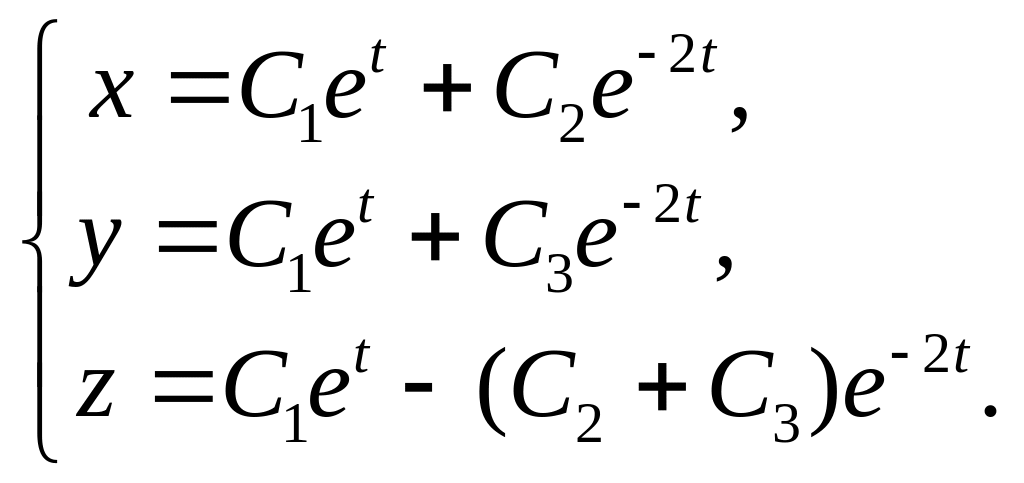 7.
7.
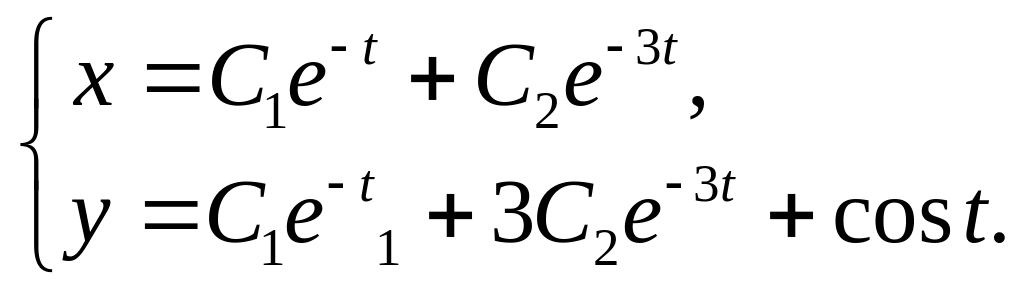
8.
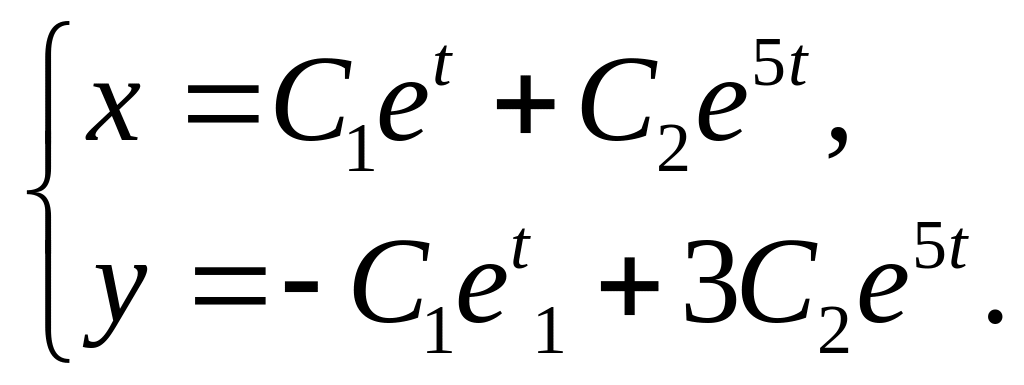 9.
9.
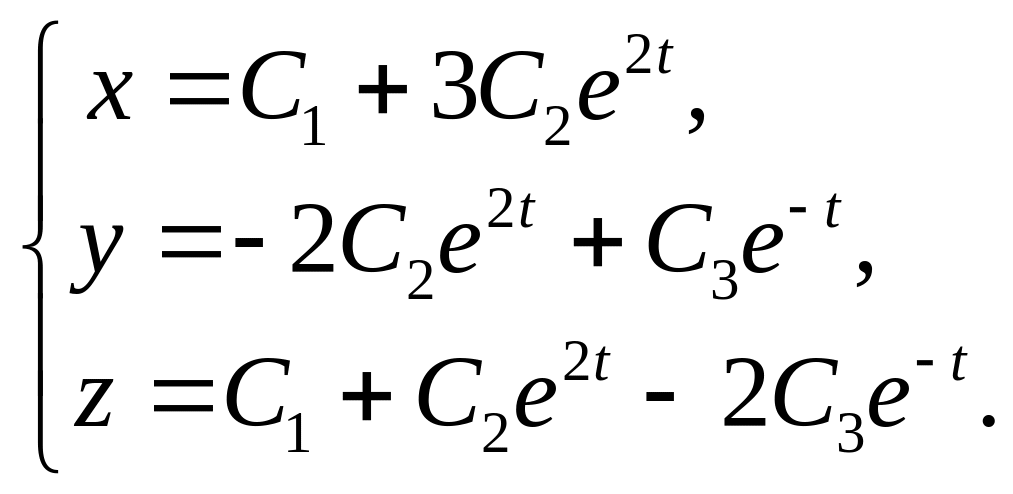
10.