ГОУВПО «Воронежский государственный технический

университет»

Кафедра высшей математики

и физико-математического моделирования

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

для организации самостоятельной работы

по изучению раздела «Дифференциальные уравнения»

курса «Математика» для студентов

направления подготовки бакалавров 230400

«Информационные системы и технологии».

очной формы обучения

Часть 2

Воронеж 2016

Составители: канд. физ.-мат. наук Е.Г. Глушко,

канд. физ.-мат. наук А.П. Дубровская,

канд. физ.-мат. наук Е.Н. Провоторова

УДК 517.9

Методические указания для организации самостоятельной работы по изучению раздела «Дифференциальные уравнения» курса «Математика» для студентов направления подготовки бакалавров 230400 «Информационные системы и технологии». очной формы обучения. Ч.2 / ГОУВПО «Воронежский государственный технический университет»; сост. Е.Г. Глушко, А.П. Дубровская, Е.Н. Провоторова. Воронеж, 2016. 34 с.

В методических указаниях содержатся краткие теоретические сведения по разделу "Дифференциальные уравнения", приводится большое количество решенных типовых задач и задачи для самостоятельного решения студентами на практических занятиях и домашних заданий. Издание соответствует требованиям Государственного образовательного стандарта высшего профессионального образования по направлению подготовки бакалавров 230400 «Информационные системы и технологии».

Библиогр.: 7 назв.

Рецензент канд. физ.-мат. наук, доц. Л.Д. Кретова

Ответственный за выпуск зав. кафедрой

д-р физ.-мат. наук, проф. И.Л. Батаронов

Печатается по решению редакционно-издательского совета

Воронежского государственного технического университета

 ГОУВПО «Воронежский государственный

технический университет», 2016

§3. Линейные дифференциальные уравнения

ВЫСШЕГО ПОРЯДКА

Линейным неоднородным дифференциальным уравнением

второго порядка называется уравнение вида

(3.1)

где функции и непрерывны на некотором отрезке .

При этих условиях существует единственное решение уравнения (3.1), удовлетворяющее заданным начальным условиям: при

Функция называется правой частью уравнения (3.1), а соответствующее уравнение называется также линейным дифференциальным уравнением второго порядка с правой частью. При приходим к линейному однородному дифференциальному уравнению второго порядка (или уравнением без правой части)

(3.2)

3.1. Линейно независимые функции

Функции и называются линейно независимыми на отрезке , если тождество

(3.3)

имеет место тогда и только тогда, когда

Если же существуют такие числа и , из которых хотя бы одно отлично от нуля, что для всех имеет место тождество (3.3), то функции и называются линейно зависимыми на отрезке .

Данные определения равносильны следующим: функции и называются линейно независимыми (зависимыми) на отрезке , если ( ), .

О линейной зависимости или независимости функций и можно судить по определителю

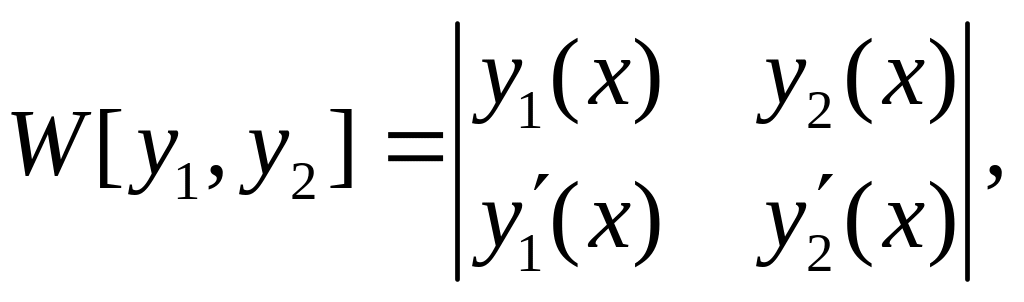
который называется определителем Вронского (или просто вронскианом).

Теорема 1. Если и линейно зависимы на отрезке , то для всех .

Теорема 2. Если и линейно независимые на отрезке решения дифференциального уравнения (3.2), то определитель Вронского этих функций отличен от нуля во всех точках отрезка .

Структура общего решения линейного дифференциального уравнения

Теорема 3. Общее решение линейного однородного дифференциального уравнения (3.2) имеет вид

где и линейно независимые решения этого уравнения.

Таким образом, для того, чтобы получить общее решение однородного уравнения (3.2), достаточно найти любые два линейно независимых частных решения этого уравнения (в этом случае говорят, что они образуют фундаментальную систему решений уравнения (3.2)).

Теорема 4. Общее решение линейного неоднородного дифференциального уравнения (3.1) представляется в виде , где - общее решение соответствующего однородного уравнения (3.2), а - некоторое частное решение неоднородного уравнения (3.1).