2 Практическая часть задание 4. Использование вычислительной техники при проведении корреляционного анализа

Постановка задачи. Сырье, поступающее из ближайшего карьера, содержат два полезных компонента - минералы А и Б. При этом в партиях сырья с повышенным содержанием А обычно обнаруживается и более высокое содержание Б, так что имеются основания ожидать, что эти величины находятся в связи друг с другом.

Анализы 10 образцов сырья, поступившего в разное время, приведены в таблице 4.1.

По индивидуальным данным (табл. 4.1) построить графики исследуемых данных.

По взаиморасположению графиков оценить коэффициент корреляции. Рассчитать коэффициент корреляции по формулам (без использования ЭВМ). Провести корреляционный анализ с помощью MathCad или Excel.

Таблица 4.1

Содержание минералов А и Б (в %)

№ варианта	№ образца	1	2	3	4	5	6	7	8	9	10
9	A (Z), %	65	55	79	61	34	26	50	46	41	45
	Б (Y), %	27	14	25	18	18	16	29	11	18	11

Решение

Построим графики исследуемых данных (рис. 4.1). О наличии или отсутствии корреляции между двумя случайными величинами качественно лучше всего судить по виду поля корреляции, поместив экспериментальные точки на координатную плоскость (рис. 4.2).

Рисунок 4.1 – Графики исходных данных

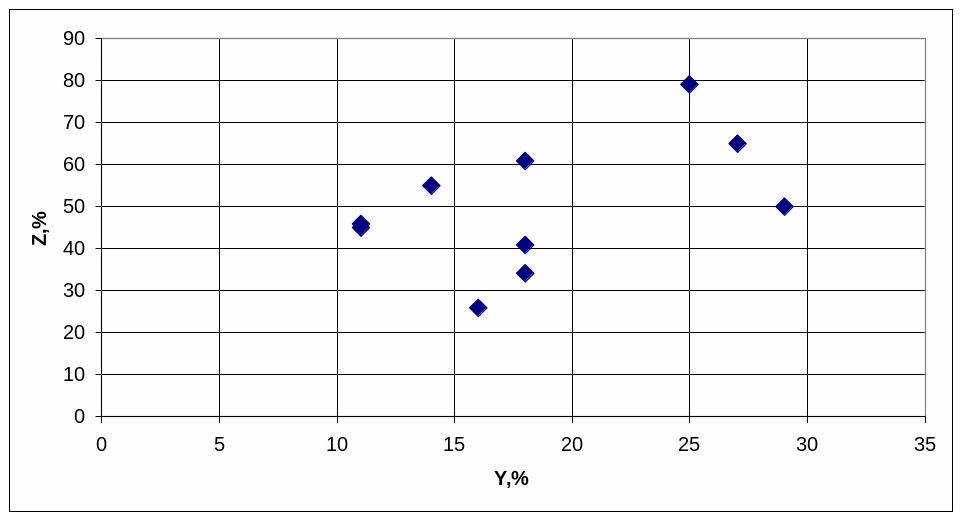
Рисунок 4.2 – Поле корреляции переменных Y и Z

По виду поля корреляции можно предположить, что в среднем с увеличением Y наблюдается увеличение Z.

Для количественной оценки тесноты связи служит выборочный коэффициент корреляции.

Коэффициент корреляции вычисляется по значениям функций отклика в области эксперимента:

(4.1)

где y_i, z_i – каждое текущее значение функции в области эксперимента;

- среднее значение функции отклика в области исследования.

Средние значения вычисляются по следующим формулам:

(4.2)

Для расчета коэффициента корреляции составим таблицу 4.2.

Таблица 4.2 - К расчету линейного коэффициента корреляции

№ п/п	zi	yi
1	65	27	14,8	8,3	122,84	219,04	68,89
2	55	14	4,8	-4,7	-22,56	23,04	22,09
3	79	25	28,8	6,3	181,44	829,44	39,69
4	61	18	10,8	-0,7	-7,56	116,64	0,49
5	34	18	-16,2	-0,7	11,34	262,44	0,49
6	26	16	-24,2	-2,7	65,34	585,64	7,29
7	50	29	-0,2	10,3	-2,06	0,04	106,09
8	46	11	-4,2	-7,7	32,34	17,64	59,29
9	41	18	-9,2	-0,7	6,44	84,64	0,49
10	45	11	-5,2	-7,7	40,04	27,04	59,29
Σ	502	187	-	-	427,6	2165,6	364,1

Рассчитаем коэффициент корреляции по формуле (4.1):

Абсолютная величина коэффициента корреляции по шкале Чеддока (таблица 4.3) 0,482 свидетельствует о том, что между исследуемыми факторами (z и y) имеется умеренная линейная статистическая связь.

Таблица 4.3 - Шкала Чеддока для коэффициента корреляции

диапазон |r|	до 0,3	0,3-0,5	0,5-0,7	0,7-0,9	выше 0,9
теснота связи	слабая	умеренная	заметная	высокая	весьма вы сокая

То есть, можно сделать вывод о наличии умеренной связи между содержанием минералов А и Б в сырье.

Далее для проведения корреляционного анализа используем вычислительную технику. При применении специальных программных продуктов для корреляционного анализа можно воспользоваться встроенными функциями.

1) Расчет в Microsoft Excel (рис. 4.3).

Рисунок 4.3 - Расчет коэффициента корреляции в Excel

При расчете в Excel была использована встроенная функция КОРРЕЛ. Данная функция имеет следующее описание:

КОРРЕЛ (массив1; массив2),

где массив1, массив2 – это интервалы значений данных, [9].

2) Расчет в MathCAD.

При расчете в MathCAD была применена встроенная функция corr(A,B), где A, В – это массивы данных.

а) Вводим массивы данных Z и Y из табл. 4.3 (рис. 4.4).

Рисунок 4.4 - Ввод данных в MathCAD.

б) Добавляем в документ функцию corr(A,B).

Для этого находим в меню Вставка пункт Функция. После этого находим необходимую функцию в категории Статистика (рис. 4.5).

Рисунок 4.5 - Добавление функции corr().

в) Вычисляем коэффициент корреляции (рис. 4.6).

Рисунок 4.6 - Вычисление коэффициента корреляции.