Решение.
Нормальное распределение имеет плотность
 ,
полагая
,
полагая
 и
и
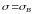 найдем теоретические вероятности по
формуле
найдем теоретические вероятности по
формуле
 .
.
Теоретические вероятности (для проверки
гипотезы о нормальном распределении
количественного признака
генеральной совокупности) можно так же
вычислять по формуле
 ,
где
,
где
 − функция стандартного нормального
распределения.
− функция стандартного нормального
распределения.
Вычисляют теоретические частоты по
формуле:
 (округляя до целого).
(округляя до целого).
Наблюдаемым значением критерия Пирсона
вычисляем по формуле
 .
.
Занесем все данные в следующую таблицу:
Номер интервала
|
Частоты
пi
|
Теоретич.
вероятности


|
Теоретич. частоты

|
Компоненты

|
1
|
1
|
0,015
|
1
|
0
|
2
|
4
|
0,070
|
3
|
0,33
|
3
|
8
|
0,192
|
10
|
0,4
|
4
|
16
|
0,296
|
15
|
0,07
|
5
|
12
|
0,258
|
13
|
0,08
|
6
|
7
|
0,127
|
6
|
0,17
|
7
|
2
|
0,035
|
2
|
0
|
|
50
|
0,992
|
50
|
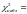 1,05
1,05
|
Наблюдаемое значение критерия равно:
 1,05.
Число степеней свободы равно:
1,05.
Число степеней свободы равно:
 .
По таблице находим:
.
По таблице находим:
 .
Так как наблюдаемое значение критерия
меньше, чем критическое (т.е. теоретическое
значение), то делаем вывод, что нет
оснований отвергнуть гипотезу о
нормальном распределении.
.
Так как наблюдаемое значение критерия
меньше, чем критическое (т.е. теоретическое
значение), то делаем вывод, что нет
оснований отвергнуть гипотезу о
нормальном распределении.


 ,
полагая
,
полагая
 и
и
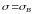 найдем теоретические вероятности по
формуле
найдем теоретические вероятности по
формуле
 .
. ,
где
,
где
 − функция стандартного нормального
распределения.
− функция стандартного нормального
распределения. (округляя до целого).
(округляя до целого). .
.



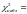 1,05
1,05 1,05.
Число степеней свободы равно:
1,05.
Число степеней свободы равно:
 .
По таблице находим:
.
По таблице находим:
 .
Так как наблюдаемое значение критерия
меньше, чем критическое (т.е. теоретическое
значение), то делаем вывод, что нет
оснований отвергнуть гипотезу о
нормальном распределении.
.
Так как наблюдаемое значение критерия
меньше, чем критическое (т.е. теоретическое
значение), то делаем вывод, что нет
оснований отвергнуть гипотезу о
нормальном распределении.