3.1. Классические методы построения математических моделей детерминированных управляющих систем

Построение адекватных математических моделей реальных управляющих систем является первоначальной задачей исследователя. На сегодня методы построения моделей систем в основном исчерпываются двумя подходами. Первый подход основан на рассмотрении системы с позиции «черного ящика». Второй подход основан на представлении управляющей системы в виде составляющих её элементов. При этом каждый такой элемент является более простой управляющей системой, для изучения которой можно применить первый подход. В работе [7] проведена простейшая классификация реальных экспериментов. Среди множества всех реальных экспериментов выделен класс так называемых детерминированных экспериментов. Наиболее просто и доступно продемонстрировать основные этапы метода построения математической модели с позиции «черного ящика» на примере изучения эволюционных детерминированных экспериментов.

Принцип построения адекватных математических моделей реальных детерминированных экспериментов с управлением с позиции «черного ящика» заключается в следующем. Пусть T есть некоторое множество. При этом произвольный элемент множества T будем называть моментом времени и обозначать через t. При каждом фиксированном t Î T выбранный элемент r(t) из некоторого заданного множества ℛ будем называть управлением в момент t и обозначать иногда ради сокращения записи через символ r. Тогда с позиции «черного ящика» любая управляющая система представляется в виде векторного параметрического по (t, r) семейства вида E_r  {(O_t, r, C_t, r): t Î T, r  ℛ}. Параметрическое по (t, r) семейство O_r  {O_t, r: t Î T, r  ℛ} и параметрическое по (t, r) семейство C_r   {C_t, r: t Î T, r  ℛ} объявляются объектом управления и соответственно системой управления. Говорят, что управляющая система E_r, объект управления O_r и система управления C_r функционируют во времени t  T при заданном управлении r(t): T  ℛ. Элемент O_t, r называется объектом управления в момент t при заданном управлении r  ℛ. Элемент C_t, r называется системой управления в момент t при заданном управлении r  ℛ. Считается, что результаты объекта управления O_r  могут не влиять на исходы системы управления C_r, а результаты системы управления C_r активно влияют на результаты объекта управления O_r. В отличие от объекта управления O_r, структура системы управления C_r существенно меняется в некотором смысле. Это означает, что при функционировании во времени t  T перед управляющей системой E ставится некоторая цель. Эта цель может быть достигнута с помощью выбора некоторым образом управления  ℛ в каждый момент времени t Î T для системы управления {C_t, r′: t Î T,  ℛ}. В этом случае управляющая система вида {(O_t, r′, C_t, r′): t Î T,  ℛ} решает поставленную цель. Здесь возникает трудная проблема выбора или построения функции вида ℛ.

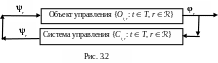
В каждый фиксированный момент времени t с помощью приборов измеряются результаты объекта управления O_r и системы управления C_r. Показания приборов в момент t для результатов объекта управления O_t, r является значением некоторого вектора _r(t)  Z, а показания приборов в момент t для результатов системы управления C _t, r является значением некоторого вектора _r(t)  Y. Здесь Z и Y некоторые заданные множества. Отсюда семейство _r  {_r(t): t  T} и семейство _r  {_r(t): t  T} являются детерминированными математическими моделями измерителей выхода объекта управления O_r и соответственно измерителей выхода системы управления C_r. Поэтому мы можем интересоваться отдельно объектом управления O_r или свойствами семейства _r и системой управления C_r или свойствами семейства _r. Более того, в общем случае семейство _r является входом (исходной основной характеристикой) для системы управления C_r, а семейство _r будет входом (исходной основной характеристикой) для объекта управления O_r. Если результаты объекта управления O_r не влияют на результаты системы управления C_r, то мы имеем дело с так называемой управляющей системой E без канала обратной связи. В противном случае эта система E функционирует с каналом обратной связи. Схема модели управляющей системы {(O_t, r, C_t, r): t Î T, r  ℛ} без канала обратной связи приведена на рис. 3.1, а схема модели управляющей системы {(O_t, r, C_t, r): t Î T, r  ℛ} с каналом обратной связи отображена на рис. 3.2. Ошибочно объявлять семейство векторов {(_r(t), _r(t)): t  T} детерминированной математической моделью управляющей системы E_r. На самом деле следующее векторное семейство {(_r(t), _r(t)): t  T} является всего лишь удобной детерминированной математической моделью совместного функционирования во времени tÎT выхода системы управления и выхода объекта управления, а не детерминированной моделью всей управляющей системы E_r в целом.

Пусть теперь функционал ((_r, _r)) со значением на прямой R определяет потери управляющей системы при управлении объектом O_r с помощью системы C_r. Тогда цель, которая ставится перед управляющей системой, состоит в нахождении оптимального управления r′  ℛ из условия

((_r′ , _r′))  inf{((_r, _r)): r  ℛ}.

Рассмотрим несколько иной случай, когда функционал ((_r, _r)) со значением на прямой R определяет доход управляющей системы Е_r при управлении объектом O_r с помощью системы C_r. В этом варианте цель, которая ставится перед управляющей системой, состоит в нахождении оптимального управления r′  ℛ из условия

((_r′ , _r′))  sup{((_r, _r)): r  ℛ}.

Другой подход основан на представлении управляющей системы в виде n составляющих её элементов. При этом каждый такой элемент рассматривается как более простая для изучения управляющая система, для которой можно с успехом применить описанный в предыдущем абзаце первый подход. При втором подходе приходится рассматривать, как правило, большое число n составляющих элементов возможно с различными основными характеристиками. Поэтому для нахождения оптимального управления системой E_r  {(O_t, r, C_t, r): t Î T, r  ℛ} необходимо решить известную проблему согласованности и «проклятия размерности» Беллмана. Другими словами, необходимо определить функциональные и статистические связи между различными характеристиками составляющих элементов системы, выделенных в большом количестве. Таковы трудности и недостатки второго подхода в построения и изучении математических моделей реальных управляющих систем. Однако иногда удается успешно преодолеть такого рода трудности и недостатки.

Проиллюстрируем эти подходы на задаче построения, анализа и оптимизации математической модели управляющей системы функционирования медицинских учреждений. С этой целью решим сначала задачу представления функционирования медицинского учреждения в виде управляющей системы без канала обратной связи.

Детальное исследование демографической ситуации в мире показывает рост числа престарелых граждан и рост заболеваемости данной категории лиц. В связи с этим требуется изучение эффективности работы существующей системы медицинских учреждений (больниц) для некоторого региона страны, например, города. С другой стороны ограничение финансовых ресурсов в здравоохранении определяет необходимость более детального исследования величины и структуры затрат на койки в каждом из многопрофильных медицинских учреждений. Более того необходимо анализировать статьи затрат лечебных учреждений по отчётным годам с точки зрения экономической классификации расходов. Было отмечено значительное изменение бюджетного финансирования даже за небольшой период функционирования такой сложной управляющей системы медицинского многопрофильного обслуживания.

В силу такого замечания представим сложную управляющую систему медицинского обслуживания для некоторого города в виде составляющих её элементов. В качестве отдельного элемента выделим медицинское учреждение M_j с номером j  1, 2, …, n. Каждое медицинское учреждение M_j при заданном управлении r(t)  ℛ функционирует в течение отчётного года, номер которого обозначим через t. При этом переменная t  {1, 2, …, k}  T. Значит, длительность всего периода наблюдений за работой больниц равна k. Медицинское учреждение M_j состоит из системы C_j, t, r   медицинского управления и из объекта O_j, t, r медицинского обслуживания. Эволюция каждого медицинского учреждения естественно является более простой управляющей системой по сравнению с функционированием всей системы многопрофильного лечения престарелых лиц региона.

Пусть теперь за каждый рассматриваемый отчетный год t для медицинского учреждения с номером j при управлении r величина x_j^(r)(t) определяет число используемых коек. Эта величина назначается системой C_j, t, r  медицинского управления и можно считать, что _{j, r} (t)  x_j^(r)(t) при заданном управлении r(t)  ℛ. Величина x_j^(r)(t) является выходом для системы C_j, t, r медицинского управления и также входом для объекта O_j, t, r медицинского обслуживания. При построении модели каждого медицинского учреждение M_j с позиции «черного ящика» не требуется знать строение сложной системы C_j, t, r медицинского управления. Поэтому множество ℛ можно не определять, а его элементы r будем использовать по необходимости и только с формальной точки зрения как индексы.

Изучим некоторые свойства объекта O_j, t, r медицинского обслуживания. При управлении r для определения компонент вектора  _{j, r}(t) выхода объекта O_j, t, r медицинского обслуживания с номером j в течение отчетного года t, прежде всего, рассмотрим структуру статей финансовых затрат. Эта структура финансирования каждого объекта медицинского обслуживания включает m статей затрат. Пусть переменная i  1, 2, …, m обозначает для каждой больницы номер статьи затрат из m возможных. Тогда при управлении r величина A_i, j^(r)(t) определяет стоимость затрат статьи с номером i для медицинского учреждения с номером j  1, 2, …, n за каждый отчетный год с номером t  1, 2, …, k. В дальнейшем величины n, k, m будем считать постоянными числами. Из множества I  {1, 2, …, m} всех номеров статей затрат выделим подмножество I₀  {i₁, i₂, … i_s} последовательных номеров i₁ < i₂ < … < i_s статей затрат, где s << m. Статьи затрат с номерами i₁, i₂, … i_s будем называть укрупненными. Итак, число укрупнённых статей затрат равно s. Как правило, финансирование любой из такого рода статей равно сумме финансирований некоторого числа заданных статей затрат с номерами из множества I \ I₀. Поэтому статьи затрат с номерами из множества I₀ естественно считать зависимыми.

В качестве примера в табл. 3.1 перечислены наименования всех возможных статей затрат. Эти статьи затрат стандартно используются в каждом отчетном году медицинскими учреждениями № 34, № 24, № 14, № 11 и № 37 Нижнего Новгорода. В этой таблице под номерами 1, 5, 16 и 17 полужирным шрифтом выделены укрупнённые (зависимые) статьи. В этом случае множество I  {1, 2, …, 25}, параметр m   25, параметр s  4 и множество I₀  {1, 5, 16, 17}. Например, финансирование укрупнённой статьи «Оплата труда и начисления на выплаты по оплате труда» под первым номером определяется суммированием финансирований статей затрат под номерами 2, 3, 4. Заметим, что множества I, I₀ и параметры m, s задаются медицинскими учреждениями. Укрупненные статьи затрат с номерами i₁, i₂, … i_s играют важную роль в изучении структуры затрат медицинских учреждений, так как эти статьи затрат определяют при управлении r суммарный объём

(3.1)

финансирования расходов по всем статьям затрат больницы с номером j в отчетном году t.

Таблица 3.1

Номер статьи	Наименование статьи затрат
1.	Оплата труда и начисления на выплаты по оплате труда
2.	Оплата труда гражданских служащих
3.	Прочие выплаты
4.	Начисления на выплаты по оплате труда
5.	Приобретение услуг, всего
6.	Оплата услуг связи
7.	Оплата транспортных услуг
8.	Оплата коммунальных услуг
9.	Освещение помещений
10.	Отопление помещений
11.	Водоснабжение помещений
12.	Услуги по содержанию имущества
13.	Капитальный ремонт
14.	Остальные расходы
15.	Прочие услуги всего
16.	Прочие расходы
17.	Поступление нефинансовых активов
18.	Увеличение стоимости основных средств
19.	Увеличение стоимости материальных запасов
20.	Приобретение продуктов питания в том числе специальные жиры
21.	Медикаменты, перевязочные средства и прочие лечебные расходы
22.	Оплата горюче-смазочных материалов
23.	Мягкий инвентарь и обмундирование
24.	Прочие расходные материалы
25.	Суммарная затрата

Для окончательного определения выхода объекта O_j, t, r медицинского обслуживания наряду с величиной A _i, j^(r)(t), которая была определена при любых фиксированных значениях i  I, j  1, 2, …, n, r  ℛ и t  T, введем величины  Q_j^(r)(t), G_j^(r)(t) и L_j^(r)(t). При заданном управлении r  ℛ больницей с номером j в течение отчетного года t  T величины  Q_j^(r)(t), G_j^(r)(t) и L_j^(r)(t) определяют число пролеченных больных, число умерших больных и количество койко-дней. Методика вычисления величин A _i, j^(r)(t), Q_j^(r)(t), G_j^(r)(t) и L_j^(r)(t) основывается на выборе так называемого нормативного управления u(t)  ℛ системой медицинского управления. Нормативное управление u  u(t) однозначно определяет количество x_j^(u)(t) используемых коек больницей с номером j в течение отчётного года t. В результате функционирования больницы с номером j в течение года t при использовании x_j^(u)(t) коек измеряются её основные показатели A _i, j^(u)(t), Q_j^(u)(t), G_j^(u)(t) и L_j^(u)(t). Эти показатели и соотношение (3.1) позволяют вычислить для больницы с номером j фактически сложившиеся нормативные коэффициенты

a_i, j(t)  A_i, j^(u)(t)/x_j^(u)(t),

(3.2)

q_j(t)  Q_j^(u)(t)/x_j^(u)(t), g_j(t)  G_j^(u)(t)/x_j^(u), l_j(t)  L_j^(u)(t)/x_j^(u)(t).

Для больницы с номером j нормативные коэффициенты a_i, j(t), a_j(t), q_j(t), g_j(t) и l_j(t) суть плотность стоимости фактических затрат статьи с номером i, плотность стоимости фактических затрат всех статей, плотность фактически пролеченных больных, плотность по факту умерших больных и плотность по факту койко-дней. Величины a_i, j(t), a_j(t), q_j(t), g_j(t) и l_j(t) являются исходной информацией в расчете на одну койку и фиксируются каждым медицинским учреждением с номером j в каждом отчетном году t. Нормативные коэффициенты в соотношении (3.2) позволяют при заданном управлении r  ℛ найти компоненты вектора _{j, r} (t) выхода объекта O_j, t, r медицинского обслуживания через значение _j, r (t)  x_j^(r)(t) его входа в виде соотношения (3.3):

 _j, r(t)  (A_1, j^(r)(t), A_2, j^(r)(t), …, A_m, j^(r)(t), Q_j^(r)(t), G_j^(r)(t), L_j^(r)(t)),

A_i, j^(r)(t)  a_i, j(t)x_j^(r)(t), Q_j^(r)(t)  q_j(t)x_j^(r)(t), G_j^(r)(t)  g_j(t)x_j^(r)(t), (3.3)

L_j^(r)(t)  l_j(t)x_j^(r)(t).

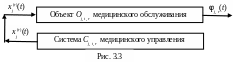
Итак, при фиксированных значениях t  T и r  ℛ схему модели управляющей системы (O_j, t, r, C_j, t, r ) медицинского учреждения M_j без канала обратной связи можно представить в виде рис. 3.3.