
- •В.И. Крылов Координатно-временные преобразования в геодезии
- •Доктор технических наук, профессор с.Н. Яшкин Московский государственный университет геодезии и картографии в.И. Крылов
- •Оглавление
- •Предисловие
- •1. Релятивистские системы координат и шкалы времени
- •1.1. Системы координат icrs, itrs и их практические реализации icrf, itrf
- •Угловые скорости вращения тектонических плит (в рад/год)
- •1.2. Четырёхмерная метрика в Солнечной системе
- •1.3. Связь промежутков барицентрического координатного времени tcb с промежутками геоцентрического координатного времени tcg
- •1.4. Связь промежутков геоцентрического координатного времени tcg с промежутками земного времени tt
- •1.5. Всемирное, звёздное и атомное время
- •Глава 2. Трёхмерные системы координат и их преобразования
- •2.1. Прямоугольные и полярные координаты
- •2.2. Преобразование координат посредством вращений
- •3.3. Преобразование прямоугольных координат с использованием углов Эйлера
- •2.4. Преобразование прямоугольных координат с использованием углов Кардано
- •Глава 3. Небесные системы координат
- •3.1 Равноденственные истинные и средние координаты
- •Лунно-солнечная нутация
- •3.2. Движение экватора и эклиптики вследствие прецессии и нутации
- •В эпоху из-за влияния нутации истинный экватор займёт положение .
- •3.3. Учёт влияния прецессии
- •3.4. Учёт влияния нутации
- •Глава 4. Земные системы координат
- •4.1. Гринвичские средние и мгновенные координаты
- •4.2. Учёт движения земных полюсов
- •4.3. Геодезические криволинейные и прямоугольные координаты
- •4.4. Связь между общеземной и референцной системами координат
- •4.5. Локальные системы координат enu
- •Глава 5. Связь между небесными и земными координатами
- •5.1. Связь между истинными равноденственными и мгновенными гринвичскими координатами
- •5.2. Преобразование координат точки, заданных в небесной системе к координатам точки в земной системе
- •5.3. Концепция невращающегося начала
- •Глава 6. История создания и современная концепция развития Российской координатной основы
- •6.1. Системы координат ск-42 и ск-95 Плановая составляющая ск-42
- •6.2. Системы координат wgs-84 и пз-90
- •7. Плоские прямоугольные координаты в проекции Гаусса-Крюгера
- •7.1 Общие положения
- •7.2. Методика вычисления прямоугольных координат Гаусса-Крюгера по криволинейным геодезическим координатам
- •7.3. Методика вычисления криволинейных геодезических координат по прямоугольным координатам Гаусса-Крюгера
- •Литература
- •П1.2. Алгоритм вычислений
- •П2. Вычисление прямоугольных координат Гаусса-Крюгера по криволинейным геодезическим координатам п2.1. Формулировка задачи
- •П2.2. Алгоритм вычислений
- •П3. Вычисление криволинейных геодезических координат по прямоугольным координатам Гаусса-Крюгера п3.1. Формулировка задачи
- •П3.2. Алгоритм вычислений
Глава 2. Трёхмерные системы координат и их преобразования
2.1. Прямоугольные и полярные координаты
В настоящее время наибольшее распространение при практическом использовании получили прямоугольные системы координат в трёхмерном пространстве, для задания которых необходимо указать положение начала, масштаб по осям координат и ориентировку осей.
В дальнейшем нам часто придётся пользоваться прямоугольными и полярными координатами, поэтому в качестве справочного материала напомним основные определения и соотношения между этими системами координат (рис. 2.1).
z
s
r
zs
O β
y
α xs
ys
x
Рис. 2.1. Прямоугольные xs, ys, zs и полярные r, α, β координаты точки s

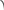

Плоскость Oxy называется основной плоскостью, а плоскость Oxz – начальной плоскостью прямоугольной системы координат. Положение точки s в прямоугольной системе координат задаётся её алгебраическими проекциями xs, ys, zs на соответствующие оси. Положение той же точки можно задать полярными координатами: r – модулем радиус-вектора точки s, - углом между осью Ox и проекцией радиус-вектора на основную плоскость, - углом между основной плоскостью и радиус-вектором. Углы и в различных координатных системах имеют свои названия, но вводятся они, как правило, описанным выше способом. Переход от полярных координат к прямоугольным координатам осуществляется по формулам
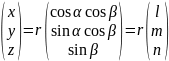 ,
(2.1)
,
(2.1)
где l, m, n – направляющие косинусы радиус-вектора.
Обратный переход от прямоугольных координат к полярным координатам можно выполнить по формулам, вытекающим из прямого преобразования (3.1)
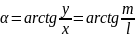 ,
(2.2)
,
(2.2)
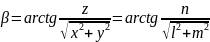 ,
(2.3)
,
(2.3)
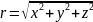 .
(2.4)
.
(2.4)
