
- •В.И. Крылов Координатно-временные преобразования в геодезии
- •Доктор технических наук, профессор с.Н. Яшкин Московский государственный университет геодезии и картографии в.И. Крылов
- •Оглавление
- •Предисловие
- •1. Релятивистские системы координат и шкалы времени
- •1.1. Системы координат icrs, itrs и их практические реализации icrf, itrf
- •Угловые скорости вращения тектонических плит (в рад/год)
- •1.2. Четырёхмерная метрика в Солнечной системе
- •1.3. Связь промежутков барицентрического координатного времени tcb с промежутками геоцентрического координатного времени tcg
- •1.4. Связь промежутков геоцентрического координатного времени tcg с промежутками земного времени tt
- •1.5. Всемирное, звёздное и атомное время
- •Глава 2. Трёхмерные системы координат и их преобразования
- •2.1. Прямоугольные и полярные координаты
- •2.2. Преобразование координат посредством вращений
- •3.3. Преобразование прямоугольных координат с использованием углов Эйлера
- •2.4. Преобразование прямоугольных координат с использованием углов Кардано
- •Глава 3. Небесные системы координат
- •3.1 Равноденственные истинные и средние координаты
- •Лунно-солнечная нутация
- •3.2. Движение экватора и эклиптики вследствие прецессии и нутации
- •В эпоху из-за влияния нутации истинный экватор займёт положение .
- •3.3. Учёт влияния прецессии
- •3.4. Учёт влияния нутации
- •Глава 4. Земные системы координат
- •4.1. Гринвичские средние и мгновенные координаты
- •4.2. Учёт движения земных полюсов
- •4.3. Геодезические криволинейные и прямоугольные координаты
- •4.4. Связь между общеземной и референцной системами координат
- •4.5. Локальные системы координат enu
- •Глава 5. Связь между небесными и земными координатами
- •5.1. Связь между истинными равноденственными и мгновенными гринвичскими координатами
- •5.2. Преобразование координат точки, заданных в небесной системе к координатам точки в земной системе
- •5.3. Концепция невращающегося начала
- •Глава 6. История создания и современная концепция развития Российской координатной основы
- •6.1. Системы координат ск-42 и ск-95 Плановая составляющая ск-42
- •6.2. Системы координат wgs-84 и пз-90
- •7. Плоские прямоугольные координаты в проекции Гаусса-Крюгера
- •7.1 Общие положения
- •7.2. Методика вычисления прямоугольных координат Гаусса-Крюгера по криволинейным геодезическим координатам
- •7.3. Методика вычисления криволинейных геодезических координат по прямоугольным координатам Гаусса-Крюгера
- •Литература
- •П1.2. Алгоритм вычислений
- •П2. Вычисление прямоугольных координат Гаусса-Крюгера по криволинейным геодезическим координатам п2.1. Формулировка задачи
- •П2.2. Алгоритм вычислений
- •П3. Вычисление криволинейных геодезических координат по прямоугольным координатам Гаусса-Крюгера п3.1. Формулировка задачи
- •П3.2. Алгоритм вычислений
Глава 5. Связь между небесными и земными координатами
5.1. Связь между истинными равноденственными и мгновенными гринвичскими координатами
Положение
внешней относительно Земли точки,
например, спутника s
можно задать и во вращающейся системе
координат её алгебраическими проекциями
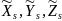 на оси системы координат
или же полярными координатами
на оси системы координат
или же полярными координатами
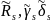 (
(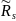 – модуль геоцентрического радиус-вектора
точки s,
– модуль геоцентрического радиус-вектора
точки s,
 - дополнение до 24 часов мгновенного
геоцентрического гринвичского часового
угла точки s,
- дополнение до 24 часов мгновенного
геоцентрического гринвичского часового
угла точки s,
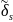 - мгновенное геоцентрическое склонение
точки s).
- мгновенное геоцентрическое склонение
точки s).
Можно
ввести также мгновенную топоцентрическую
гринвичскую систему координат,
отличающуюся от мгновенной геоцентрической
гринвичской системы лишь положением
начала, которое в этом случае совмещается
с пунктом земной поверхности, тогда
положение точки задаётся прямоугольными
координатами
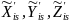 либо полярными координатами
либо полярными координатами
 .
.
Различие в ориентировке осей истинной равноденственной и мгновенной гринвичской систем координат вызвано суточным вращением Земли вокруг своей оси (рис. 5.1). Переход от координат к координатам осуществляется единственным поворотом вокруг оси аппликат на угол, равный часовому углу истинной точки весеннего равноденствия относительно истинного начального меридиана. А этот угол, как известно, является мерой истинного гринвичского звёздного времени S.
Таким образом, рассматриваемое преобразование координат будет выражаться следующими формулами
 ,
(5.1)
,
(5.1)
где
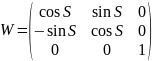 - матрица суточного вращения Земли.
- матрица суточного вращения Земли.
Истинное
звёздное гринвичское время
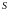 вычисляется по формуле (1.27).
вычисляется по формуле (1.27).
Z
![]()
O Y
G
X
S
Рис. 5.1. Средняя OXYZ, мгновенная гринвичские системы координат и истинная равноденственная система координат
Координаты
Небесного промежуточного полюса в
земной системе координат называются
координатами полюса
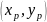 .
.
Угол, на который Земля поворачивается относительно Небесного промежуточного полюса за определённый промежуток времени, называется гринвичским истинным звёздным временем S. С помощью точной процедуры гринвичское истинное звёздное время S может быть преобразовано во Всемирное время UT1 (и наоборот UT1 в S).
