В эпоху из-за влияния нутации истинный экватор займёт положение .
Точка
пересечения истинного экватора и
подвижной эклиптики называется истинной
точкой весеннего равноденствия в эпоху
.
При этом угол наклона
называется истинным наклоном эклиптики
к экватору в эпоху
.
Составляющие нутации в долготе
и в наклонности
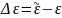вычисляются по формулам (3.1) и (3.2)
соответственно.
3.3. Учёт влияния прецессии
Пусть
заданы средние равноденственные
геоцентрические координаты точки s
в системе координат
,
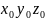определённой на эпоху
.
В качестве эпохи
для определённости примем стандартную
эпоху
.
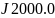Требуется вычислить средние равноденственные
геоцентрические координаты той же точки
s
в системе координат xyz,
определённой на другую эпоху t.
Различие в ориентировке осей рассматриваемых
систем координат вызвано влиянием
прецессий экватора и эклиптики (рис.
3.4).
z z0
x0
y0 y
x
Рис.
3.4. Две средние равноденственные системы
координат:
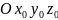на
эпоху
и Oxyz
на эпоху t
Напомним, что под влиянием прецессии экватора средняя точка весеннего равноденствия эпохи перемещается в плоскости начальной эклиптики по дуге большого круга и в эпоху t занимает положение . Под влиянием прецессии эклиптики средняя точка весеннего равноденствия перемещается в плоскости среднего экватора эпохи t и занимает положение .
Преобразование координат произвольной точки, определённой в средней равноденственной системе координат эпохи к координатам той же точки, но в средней равноденственной системе координат xyz эпохи t можно осуществить посредством четырёх поворотов по формулам
.
(3.3)
Прецессионные параметры в соответствии с моделью МАС 2000 вычисляются по формулам, полученным Капитейн [17]:
;
;
;
;
.
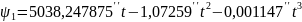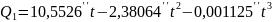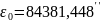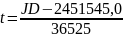Вместо рассмотренных четырёх поворотов можно обойтись тремя поворотами, если ввести прецессионные параметры Ньюкома-Андуайе, аналогичные углам Эйлера и связанные с ними соотношениями:
.
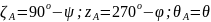Углы
Ньюкома-Андуайе показаны на рис. 3.5. Они
вводятся следующим образом. Угол
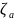– угол между осью
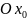и линией пересечения плоскостей
и
.
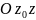Угол
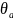- двугранный угол между плоскостями
и
или плоский угол между осями
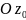и
.
Угол
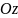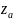- угол между линией пересечения плоскостей
и
и осью
.
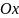z0
z
O
y0
x0
y
x
Рис. 3.5. Прецессионные углы Ньюкома-Андуайе
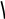
Эти три поворота представляются в виде:
.
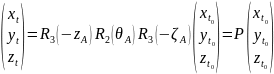(3.4)
Сами же прецессионные параметры Ньюкома-Андуайе вычисляются по формулам модели прецессии-нутации МАС 2000:
;
.
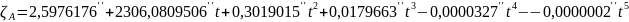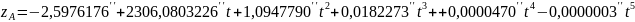Здесь t выражено в юлианских столетиях, отсчитываемых от эпохи J2000.0 .