
- •Байесовские сети доверия (BayesianBeliefNetworks, 1998,Pearl)
- •Другой вариант подсчёта
- •Метод субъективных коэффициентов уверенности
- •Методы обработки неопределённостей в guru
- •Использование нечёткой переменной.
- •Поиск решений в условиях неопределенности с использованием Дерева Решений (др) Конъюнктивная вершина
- •Теория свидетельств Демпстера-Шефера
- •Посылки теории свидетельств
- •Правило объединения свидетельств.
- •Вероятностная логика
- •Оперирование с неопределённостью лингвистического характера
- •Операция контрастной интенсификации
- •Элементы сос тепенями принадлежности 0.5 не затрагиваются, всё, что меньше – сдвигается к левому краю, всё, что больше – к правому.
- •Операция увеличения нечёткости
- •Операции на шкалах
Использование нечёткой переменной.
Нечёткая переменная может одновременно принимать несколько значений.
E.IFUZ = <n>
Пример
 = (200 cf
90, 100 cf
30)
= (200 cf
90, 100 cf
30)
 = (150cf
80, 50 cf
20)
= (150cf
80, 50 cf
20)
P1
=(
 >
>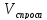
 цена = ‘↓’)
цена = ‘↓’)
P2
=
 <
<
 цена = ‘↑’)
цена = ‘↑’)
P3
=
 =
=
 цена = '=’)
цена = '=’)
Что
ожидать от таких данных, если прогнозируются
 и
и
Классической логикой нечётких переменных является логика Заде.
cf
( >
> )
= max{min(0,9; 0,8), min(0,9; 0,2), min(0,3; 0,2)} = 80
)
= max{min(0,9; 0,8), min(0,9; 0,2), min(0,3; 0,2)} = 80
cf
( <
< )
= min{80; 30} = 30
)
= min{80; 30} = 30
Цена = {‘↑’cf 30, ‘падает’ cf 80, 'не изменяется’ cf 0}
Одна переменная может принять ряд значений с соответствующими степенями принадлежности.
Пример
Построение прогнозирующей системы для банка. Характеристики клиента:
Возраст
Семейное положение
Профессиональный статус
Вклад – нечёткая переменная.
Правила:
P1
= (возраст < 20 вклад
вклад = (‘образование’cf
40, ‘жильё’ cf
10, ‘сбережения’ cf 5))
= (‘образование’cf
40, ‘жильё’ cf
10, ‘сбережения’ cf 5))
P2
= (возраст ≥ 20 & возраст < 30 вклад
вклад = (‘образование’cf
20, ‘жильё’ cf
20, ‘сбережения’ cf 10))
= (‘образование’cf
20, ‘жильё’ cf
20, ‘сбережения’ cf 10))
P3
= (семейное положение = ‘одинокий’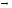 вклад
вклад = (‘образование’cf
30, ‘жильё’ cf
10, ‘сбережения’ cf 20))
= (‘образование’cf
30, ‘жильё’ cf
10, ‘сбережения’ cf 20))
P4=
(семейное положение = ‘семейный’ вклад
вклад =
(‘образование’cf
10, ‘жильё’ cf
40, ‘сбережения’ cf 20))
=
(‘образование’cf
10, ‘жильё’ cf
40, ‘сбережения’ cf 20))
P5
= (профессия= ‘рабочий’ вклад
вклад = (‘образование’cf
20) ; вклад
= (‘образование’cf
20) ; вклад = (‘образование’cf
60))
= (‘образование’cf
60))
Дано:
(Возраст < 20; семейное положение = ‘семейный’; профессиональный статус = ‘рабочий’)
Последовательность действий GURU при выборе логики PP:
|
|
P1
|
P5 |
Σ |
P5
|
|
|
Образование |
40 |
10 |
46 |
-60 |
18 |
|
Жильё |
10 |
40 |
46 |
|
46 |
|
Сбережения |
5 |
20 |
24 |
20 |
39 |


Σ =( a + b – a*b)/100% a + b – a*b/100%
Ответ:
Вклад = (‘образование’ cf 18, ‘жильё’ cf 46, ‘сбережения’ cf 39) -в сумме 100%
Нормировка к 100%:
Вклад = (‘образование’ 17,6% , ‘жильё’ 44,6%, ‘сбережения’ 37,8%)
ММ: Вклад = (‘образование’ cf (40-60) , ‘жильё’ 40, ‘сбережения’ cf 20)
Лекция №8 (1.11.11)
Поиск решений в условиях неопределенности с использованием Дерева Решений (др) Конъюнктивная вершина

Если
 ,
можно констатироватьRс
вероятностьюk.
,
можно констатироватьRс
вероятностьюk.
R



 …
…
а) Логика maxmin.
K(R)=min {k(Ci), k(Cj)}* k
Если длинная конъюнкция, то
K(R)=min{k(Ci), …, …, …,k(Cj)}*k
b) Вероятностная логика.
K(R)=k(Ci)*k(Cj)*k
Дизъюнктивная вершина
R



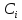 …
…  …
…
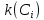 k(
k( k(
k(
а) Логика maxmin.
K(R)=max{ *
* ,
,
 *
* ,
…}
,
…}
b) Вероятностная логика.
Упорядочиваем свидетельства по важности и включаем дополнительное:
K(R)=

K(R)=



Пример
{Pi} – набор правил,
{Fj} – наблюдаемые факторы,
{Сi} – множество промежуточных заключений,
R– целевое заключение.
P1 = (F1 C1 ; 0.8)
P2 = (F2 C1 ; 0.7)
P3 = (F3 C2 ;1)
P4 = (F4 & F5 C3 ; 0.9)
P5 = (F6 C6 ;1)
P6 = (F7 C6 ; 0.7)
P7 = (F8 & F9 C4 ; 0.4)
P8 = (C1 & C2 & C3 C5 ; 0.9)
P9 = (C4 C6 ; 0.8)
P10 = (C5 & C6 R ; 1)
Если дерево оборвалось на промежуточном заключении и нет правила, позволяющего его связать, то база не полна.
R

P10 ; 1
C6
C6






P8 ; 0.8 P5 ; 1 P6 ; 0.7 P9 ; 0.8
C1
C2
C3
F6
F7
C4






P1
; 0.8
P2
; 0.7
P3
;1
P4
; 0.9
P7
; 0.4

F1 F2 F3 F4 F5 F8 F9
В дереве проиллюстрировано, что есть связь между наблюдаемыми вершинами и целевым заключением.
 ,
i =
,
i =

k(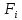 )
)
 -
коэффициент уверенности наблюдаемого
фактора
-
коэффициент уверенности наблюдаемого
фактора
 k(
k(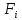 ),
k(
),
k( )
Є [0,1]
)
Є [0,1]
Sн = (0,9; 0; 1; 0,8; 0,9; 0,1; 0,8; 0,7; 0,5)
F1 F2 F3 F4 F5 F6 F7 F8 F9
а) maxmin
k(C1) = max{(0.9*0.8); (0.7*0)} = 0.72
k(C2) = 1
k(C3) = min{0.8; 0.9)*0.9 = 0.72
k(C4) = min{0.7; 0.5)*0,4 = 0.2
k(C5) = min{0.72; 1; 0.72)*0.9= 0.65
k(C6) =max{(0.7*0.8); (0,8*0.2)} =0.56
k(R) =min{0.65; 0.56)*= 0.56 (56%)
б) вероятностная логика
k(C1) = 0.8*0.9 = 0.72
k(C2) = 1
k(C3) = 0.9*0.8*0.9 = 0.65
k(C4) = 0.5*0.7*0.4 = 0.14
k(C5) = 0.72*1*0.65*0.9 = 0.42
k(C6) = 0.8*0.7 + 0.14*0.8 – 0.56*0.12 =0.57
k(R) = 0,42*0.57*1 = 0.24 (24%)
Пусть теперь нашли ещё одного эксперта, который считает по своим правилам:
Тогда:
а) k(R) = 0.6
k(R) =max{0.56*0.6} = 0.6
а’)k(R) = 0.5
k(R) =max{0.56*0.5} = 0.56
б) k(R) = 0.6
k(R) = 0.24 + 0.6 – 0.24*0.6 = 0.7
б’) k(R) = 0.5
k(R) = 0.7 + 0.5 – 0.7*0.5 = 0.85
В случае maxminпривлечение дополнительных правил ничего не изменило, а в случае вероятностной логики – существенно повлияло. Значит, надо тщательнее выбирать логику.
