4 Силовой расчет рычажного механизма

4.1 Определение внешних сил, действующих на звенья механизма

Определим силы давления воздуха на поршни. Так как машина в данной работе является рабочей, то силы, действующие на поршни, являются силами полезного сопротивления.

На рисунке 4 построен план механизма при угле поворота кривошипа ₁ = 60 º в масштабе _l = 0,01 м/мм. Отметим на этом плане механизма ход точек В и С: S_Bmax и S_Cmax. На отрезках, соответствующих ходу точек В и С, построим индикаторные диаграммы давления воздуха. Диаграммы строим в безразмерных координатах «S/S_max - p/p_max». Числовые данные берем из таблицы 2 задания.

В указанном положении при угле поворота кривошипа _ = 60 º в левом цилиндре (II ступень) идет всасывание, в правом цилиндре (I ступень) – сжатие. Силу давления, действующую на 3 звено в 1-ом цилиндре, определяем по формуле:

,

(8)

где – давление в I ступени цилиндра, определяется по индикаторной диаграмме, Па.

Для данного положения точки В с индикаторной диаграммы I цилиндра получаем:

,

(9)

откуда

.

Значение дано в задании. Вычислим силу давления в I ступени:

.

Рисунок 4 – Графическая часть расчетно-графической работы

Точно так же определяем силу давления газа на поршень 5:

,

(10)

где – давление во II ступени цилиндра, определяется с использованием индикаторной диаграммы, МПа.

Так как во II ступени цилиндра совершается такт всасывания, то из точки С механизма «опускаемся» до линии всасывания и получаем

.

(11)

Отсюда

.

Вычислим силу давления воздуха на ползун 5:

.

Вычислим силы тяжести всех звеньев, принимая ускорение свободного падения g 10 м/c² :

; ; ; .

Определим силы инерции звеньев и инерционные моменты. Модули этих величин определяются следующим образом:

; ; ; ; ; .

Все вычисленные инерционные силовые факторы (силы и моменты) направлены противоположно ускорениям, использованным в формулах.

4.2 Определение реакций в кинематических парах групп Ассура.

Силовой анализ в многозвенном механизме нужно начинать с групп Ассура, наиболее удаленных по кинематической цепи от входного звена. В нашем примере силовой анализ можно начать с любой из двух равноудаленных групп Ассура. Изобразим группы Ассура, состоящие из звеньев 2, 3 и 4, 5 на листе в том положении, в котором они находятся в составе механизма.

Начнем силовой анализ с группы Ассура, состоящей из звеньев 2 и 3. Приложим к этим звеньям все известные силы: , , . Кроме того, приложим инерционные силовые нагрузки. Прикладываем силы инерции и моменты сил инерции к звеньям механизма. Силу прикладываем в точке S₂, силу инерции - в точке В. Направляем их параллельно и противоположно ускорениям точек, в которых они приложены. Момент сил инерции направляем противоположно угловому ускорению .

Производим замену двух инерционных силовых факторов: силы инерции и момента сил инерции , одной результирующей силой , равной по величине и направлению силе , но приложенной в некоторой точке Т₂ звена АВ или на его продолжении. Чтобы определить точку Т₂ , выполним следующие действия. Сначала вычисляем плечо по формуле:

.

Теперь сносим силу параллельно самой себе на плечо . На пересечении линии действия перенесенной силы и оси звена АВ определим точку Т₂.

Изобразим реактивные силы. Действие звена 1 и стойки 6 заменяем неизвестными реакциями и . Реакцию для удобства вычислений раскладываем на две составляющие: - вдоль оси звена 2, и , перпендикулярно звену. - сила реакции действует со стороны стенки цилиндра на поршень 3, направлена перпендикулярно оси цилиндра.

Определяем величину реакции . Для этого составляем уравнение суммы моментов всех сил, действующих на звено 2, относительно точки В:

,

(12)

откуда

.

Реакции и определим построением силового многоугольника, решая векторное уравнение равновесия, составляем для звеньев 2,3:

.

(13)

Построим план сил. Из произвольной точки а в масштабе откладываем последовательно все известные силы , , , , , , перенося их параллельно самим себе в план сил. Так как силы тяжести , в масштабе получаются меньше 1 мм, то мы их не откладываем. Через конец последнего из суммируемых векторов проводим линию параллельно вектору до пересечения с прямой, проведенной из точки а параллельно вектору . Точка пересечения этих прямых замкнет векторный многоугольник. Укажем стрелками направление векторов и в соответствии с направлением обхода. Тогда, измеряя полученные векторы, получим

; ,

где , – длины отрезков на плане сил, мм.

Аналогично определяем реакции и в другой группе Ассура, состоящей из звеньев 4,5. Прикладываем к звеньям 4,5 все известные силы , , , , . Силу инерции и момента сил инерции заменяем векто-

ром силы точно так же, как это делали ранее для звеньев 2, 3. Плечо вычисляем по формуле:

.

Сносим силу параллельно самой себе на величину и находим точку Т₄. Отбрасывая связи, заменяем их реакциями и , а также . Намечаем плечи и . Составляем уравнение суммы моментов всех сил, действующих на звено 4, относительно точки С:

.

(14)

Из этого выражения вычисляем :

.

Для определения модулей реакций и строим план сил по уравнению:

.

(15)

В уравнении (15) неизвестны реакции и по модулю. Известно направление реакции вдоль звена АС, а реакции - перпендикулярно ОС. Остальные силы в уравнении известны и по модулю, и по направлению. Откладываем известные силы последовательно друг за другом, начиная с в масштабе . и определяем при пересечении прямых, проведенных из начала и конца построения соответственно, параллельно векторам этих сил. Изображаем на плане сил вектор , имея в виду, что

.

(16)

Измеряя длины векторов на чертеже, вычислим силы реакции и :

; ,

где , - длины векторов на плане сил, мм.

4.3 Силовой расчет входного звена

Изображаем входное звено (рисунок 4). Прикладываем к звену 1 в точке А силы , , а также пока еще неизвестную уравновешивающую силу . Уравновешивающую силу приложим в точке А и направим перпендикулярно кривошипу ОА. Так как центр масс кривошипа совпадает с осью вращения, точкой О, то сила инерции . Поскольку угловая скорость первого звена , то момент сил инерции .

Вначале составляем уравнение моментов всех сил относительно точки О:

.

(17)

Из этого уравнения найдем уравновешивающую силу :

.

В шарнире О со стороны стойки 6 на звено 1 действует реакция (изобразим пунктирной стрелкой), которую определяем построением многоугольника сил согласно векторному уравнению:

.

(18)

Откладываем последовательно известные силы , , в масштабе . Так как сила тяжести в масштабе получается меньше 1 мм, мы ее не откладываем, т.е. пренебрегаем ею. Соединив начало с концом получим реакцию :

,

где - длина отрезка на плане сил, мм.

4.4 Определение уравновешивающей силы методом Н. Е. Жуковского

Строим повернутый по часовой стрелке на 90º план скоростей (рисунок 4). В одноименные точки плана переносим все внешние силы в строгом соответствии с их направлением (без масштаба), действующие на звенья механизма, в том числе и силу . Составляем уравнение моментов всех сил относительно полюса плана скоростей р, плечи сил измеряем в мм непосредственно на чертеже:.

(19)

Из этого уравнения найдем уравновешивающую силу :

Определим относительное расхождение результатов определения уравновешивающей силы, полученных методом Жуковского и методом планов сил

.

Различие в значениях уравновешивающей силы, вычисленной методом плана сил и с помощью рычага Жуковского, составляет менее 5 %, что свидетельствует о правильности расчетов.

Список литературы

1 Лапшин П. Н., Манило И. И. Стандарт предприятия. Учебно-методическая документация. Общие требования к оформлению. – Курган: КГСХА, 2006. – 35 с.

2 Лачуга Ю. Ф., Воскресенский А. Н., Чернов М. Ю. Теория механизмов и машин. Кинематика, динамика и расчет. – М.: Колос, 2008. – 304 с.

Приложение А

Титульный лист расчетно-графической работы

ФГБОУ ВПО «Курганская государственная сельскохозяйственная

академия им. Т. С. Мальцева»

Факультет	инженерный (или промышленного и гражданского
	строительства)
Кафедра	теоретической механики
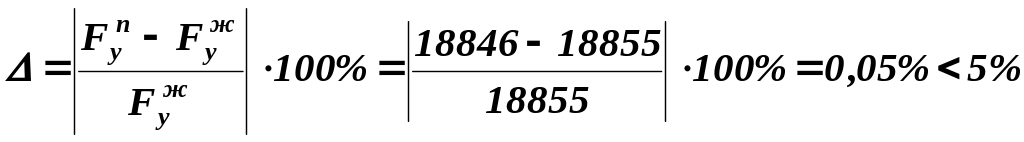