2.2.3.2. Нормальная имплантация однородных полупроводниковых подложек с учетом эффекта каналирования
Для исследования эффекта каналирования при имплантации примесей в монокристаллические кремниевые подложки разработан командный файл для модуля DIOS (листинг 2.7).
Листинг командного файла 2.7
Тitle ('Implantation - 2')
grid (x=(0.0, 1.5), y=(-1.0, 0.0), nx=40)
replace (сontrol(ngra=1))
graph (triangle=off, plot)
substrate (orientation=110, element=P, conc=1e13, ysubs=0.0)
implant(element=B, dose=6.25e15, energy=60kev, func=p4s)
1D(Rs=on, xsect(1.5))
1D(file=n@node@, species(netactive), xsect(1.5), fac=-1)
save(file='n@node@', type=mdraw, compress=off)
end
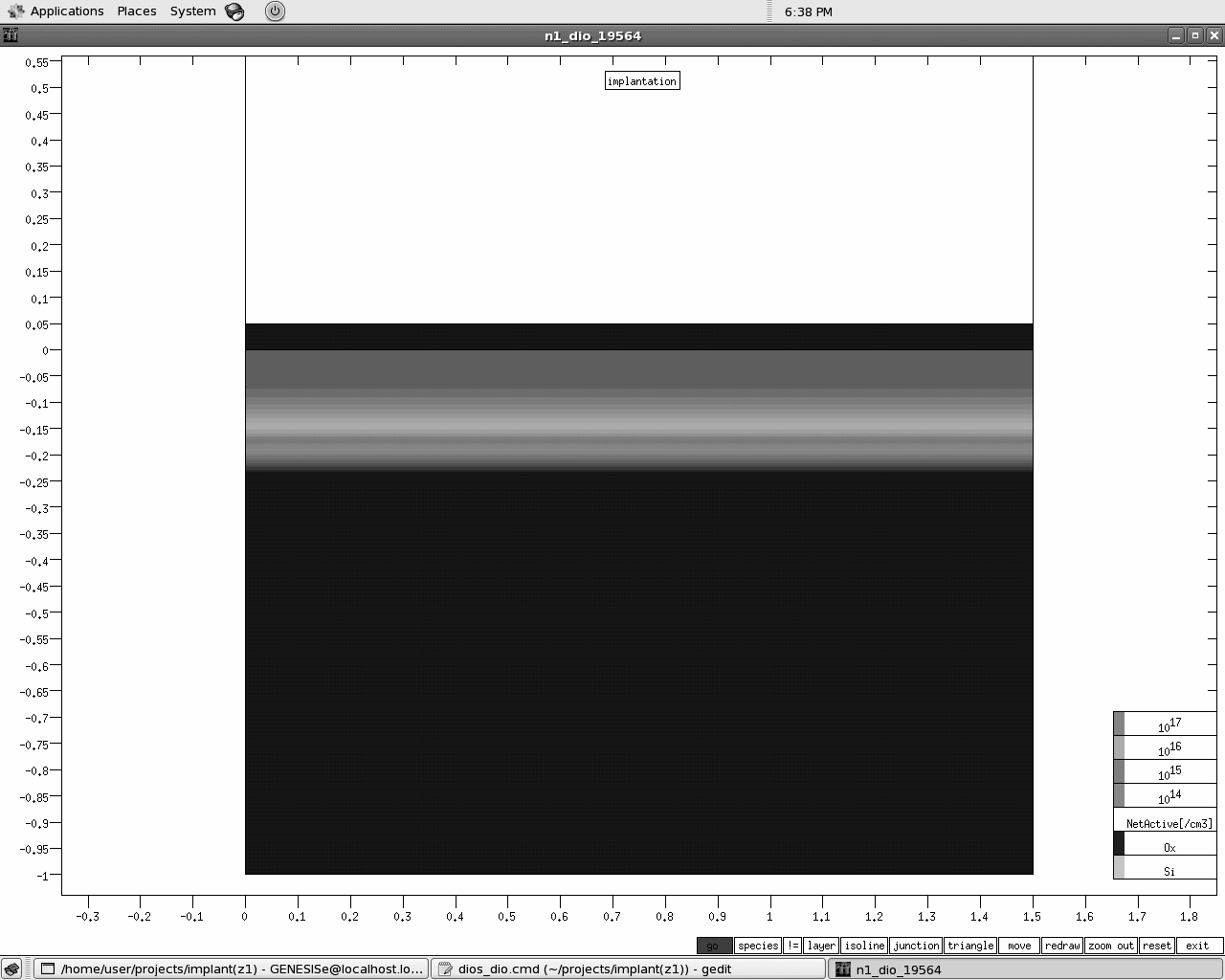
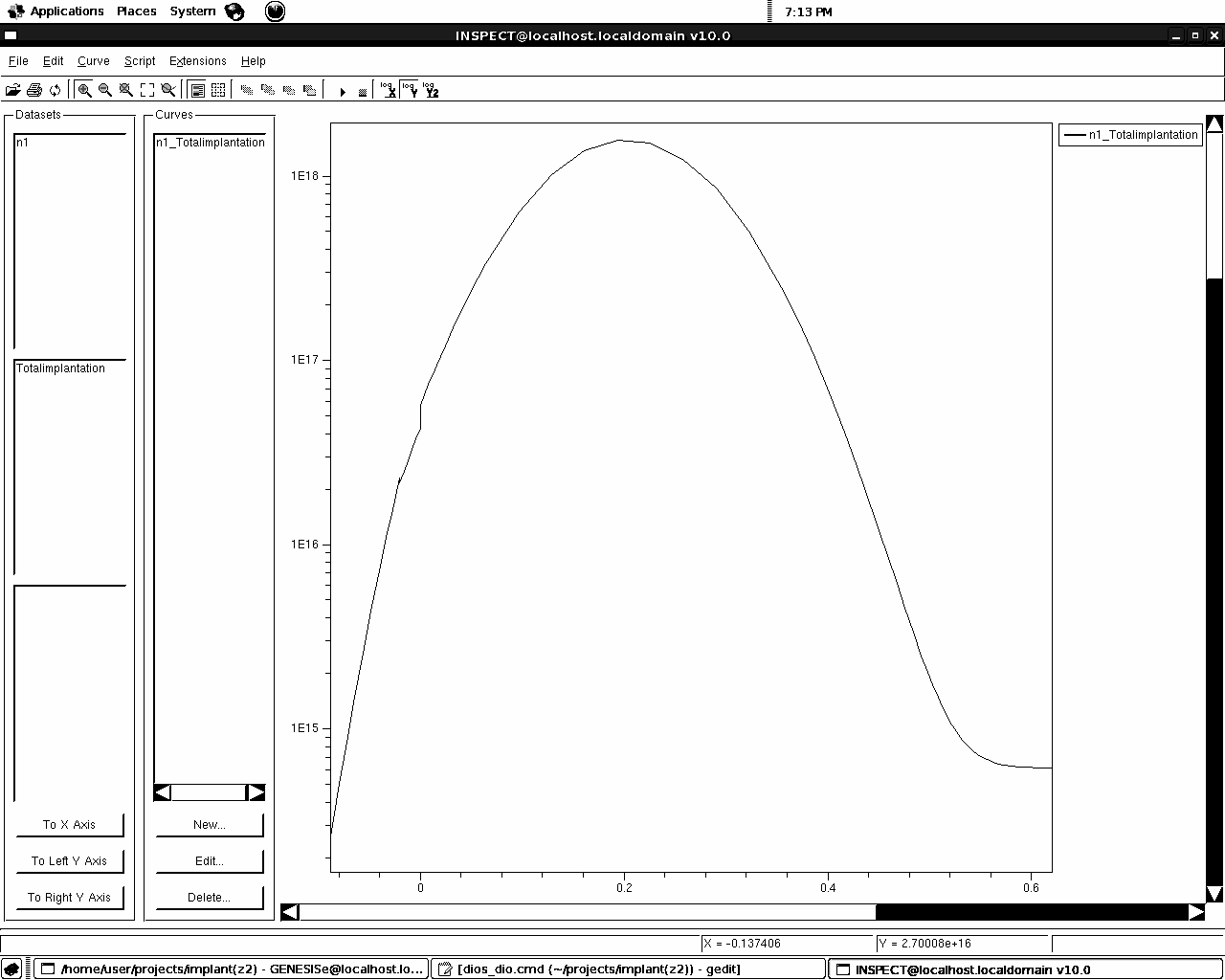
Структура, получаемая в результате моделирования с командным файлом из листинга 2.7, показана на рисунке 2.23. На рисунках 2.24, 2.25 и 2.26 представлены концентрационные профили имплантированного бора, фосфора и мышьяка соответственно, полученные с использованием разных аппроксимирующих функций для основного профиля и «хвоста» распределения.
|
|
Рис. 2.23. Структура после ионной имплантации с учетом эффекта каналирования |
Рис. 2.24. Концентрационные профили ионно-имплантированного бора, рассчитанные по модели: 1 - симметричного гауссовского распределения; 2 - Пирсон-4; 3 - Пирсон-4 с учетом линейного экспоненциального «хвоста»; 4 - Пирсон-4 с учетом нелинейного экспоненциального «хвоста» |
Рис. 2.25. Концентрационные профили ионно-имплантированного фосфора, рассчитанные по модели: 1 - симметричного гауссовского распределения; 2 - Пирсон-4;
3-4 - Пирсон-4 с учетом линейного и нелинейного экспоненциального «хвоста»
Рис. 2.26. Концентрационные профили ионно-имплантированного мышьяка, рассчитанные по модели: 1 - симметричного гауссовского распределения; 2 - Пирсон-4;
3-4 - Пирсон-4 с учетом линейного и нелинейного экспоненциального «хвоста»
2.2.3.3. Имплантация многослойных структур
Для исследования распределений ионно-имплантированных примесей в многослойных структурах созданы два командных файла для имплантации двухслойных структур SiO2-Si (командный файл 2.8) и трехслойных структур Si3N4-SiO2-Si (командный файл 2.9).
Листинг командного файла 2.8
Тitle ('Implantation - 3')
grid (x=(0.0, 1.5), y=(-1.0, 0.0), nx=40)
replace (сontrol(ngra=1))
graph (triangle=off, plot)
substrate (orientation=100, element=P, rho=7.5, ysubs=0.0)
deposit(material=ox, thickness=0.02)
implant(element=B, dose=5/1.6e-13, energy=100kev, func=gauss)
1D(Rs=on, xsect(1.5))
1D(file=n@node@, species(total), xsect(1.5), fac=-1)
save(file='n@node@', type=mdraw, compress=off)
end
Листинг командного файла 2.9
Тitle ('Implantation - 4')
grid (x=(0.0, 1.5), y=(-1.0, 0.0), nx=40)
replace (сontrol(ngra=1))
graph (triangle=off, plot)
substrate (orientation=100, element=P, rho=7.5, ysubs=0.0)
deposit(material=ox, thickness=0.02)
deposit(material=Si3N4, thickness=0.07)
implant(element=B, dose=5/1.6e-13, energy=100kev, func=gauss)
1D(Rs=on, xsect(1.5))
1D(file=n@node@, species(total), xsect(1.5), fac=-1)
save(file='n@node@', type=mdraw, compress=off)
end
Структура, получаемая в результате моделирования имплантации бора в кремний через оксидный слой, показана на рисунке 2.27, а на рисунках 2.29-2.30 приведены расчетные концентрационные профили бора и фосфора соответственно.
На рисунке 2.28 показана структура, получаемая в результате моделирования имплантации бора в кремний через слои нитрида и оксида кремния, а на рисунке 2.31 приведен концентрационный профиль имплантированного бора.
|
|
Рис. 2.27. Структура SiO2-Si, легированная бором |
Рис. 2.28. Структура Si3N4-SiO2-Si, легированная бором |
|
|
Рис. 2.29. Распределение концентрации имплантированного бора в структуре SiO2-Si |
Рис. 2.30. Распределение концентрации имплантированного фосфора в структуре SiO2-Si |
|
|
а) |
б) |
Рис. 2.31. Распределение концентрации имплантированного бора в структуре Si3N4-SiO2-Si (а) и увеличенный фрагмент распределения (б) |
|
