Определение погрешности мёртвого хода кинематической цепи:

Общая погрешность мёртвого хода состоит из люфтовой погрешности цепи и упругого мёртвого хода валов:

(53)

Определение люфтовой погрешности передачи:

Определим по таблицам собственную люфтовую погрешность Δφ_7G для передачи c 7 степенью точности, сопряжением G и модулем m=0.4 мм.

Определим собственную люфтовую погрешность для разрабатываемой конструкции по формуле:

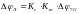(54)

Где K_c – коэффициент, вносящий поправку при выборе степени точности 7G, K_c = 1,6; \\кхм-кхм

K_m - коэффициент, вносящий поправку для модуля m=1 мм, K_m = 1,2;

Результаты представим в сводной таблице (табл.9):

Табл.9. Результаты расчета погрешности мертвого хода

№ ступени	1	2	3	4	5
zколеса	58	58	58	58	58
a, мм	39	39	39	39	39
Δφ`7G	7	7	7	7	7
Δφ`л	13,44	13,44	13,44	13,44	13,44

Найдём люфтовую погрешность передачи по формуле:

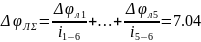(55)

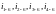
Здесь 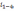и 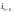– передаточные отношения от валов редуктора к выходному валу.

Определение упругого мёртвого хода валов:

Т.к. в качестве материала для валов используется сталь, то упругий мёртвый ход вала в угловых минутах считаем по формуле:

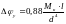(56)

Результаты представим в сводной таблице (табл.10):

Табл.10 Значение упругого мёртвого хода ступеней редуктора
№ вала	1	2	3	4	5
Mк, Н∙мм	0,55	1.54	4.29	11.93	33.25
l, мм	38.05	38.05	38.05	38.05	38.05
d, мм	3,0	3,0	3,0	3,0	3,0
Δφ`у	0,227	0,63	1.77	4.93	13.73

Определяем суммарную величину упругого мёртвого хода:

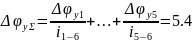(57)

Суммарная величина мёртвого хода:

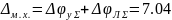
Определение кинематической погрешности передачи:

Кинематическую погрешность зубчатого колеса рассчитываем по формуле:

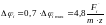(58)

Где – допуск на кинематическую погрешность зубчатых колёс, (59) .

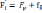Здесь F_р – допуск на накопленную погрешность шага зубчатого колеса (шестерни), выбирается из таблиц; f_f – допуск на погрешность профиля зуба (f_f = 11 , т. к. m = 1 и степень точности 7).

Результаты представим в сводной таблице (табл.11):

Табл.11 кинематической погрешности колёс редуктора
№	1	2	3	4	5	6	7	8	9	10
Z	20	58	20	58	20	58	20	58	20	58
da, мм	7,6	23,6	7,6	23,6	7,6	23,6	7,6	23,6	7,6	23,62
Fp	22	26	22	26	22	26	22	26	22	26
Fi`	31	35	31	35	31	35	31	35	31	35
Δφ`i	21,9	7,4	21,9	7,4	21,9	7,4	21,9	7,4	21,9	7,4

Суммарную кинематическую погрешность передачи вычислим по формуле:

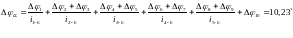(59)

Общая погрешность передачи:

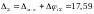
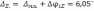≤ 20`

Таким образом, спроектированная передача удовлетворяет условию точности.