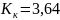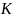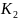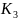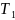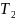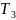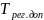Оглавление

Исходные данные: 3

1. Анализ системы автоматического управления. 3

1a. Исследование заданной системы на устойчивость двумя критериями. 3

2. Синтез системы автоматического управления 6

2а. Определение требуемого коэффициента передачи синтезируемой САУ 6

2б. Синтез корректирующих устройств методом логарифмических частотных характеристик. 7

3. Проверка результатов синтеза 10

3а. Определение запасов устойчивости скорректированной САУ 10

3б. Оценка качества скорректированной системы аналитическим методом. 13

в. Построение структурной схемы корректирующего устройства………………………….14

Исходные данные:

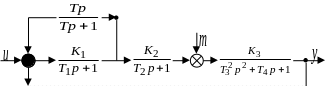
Рисунок 1– Структурная схема линейной САУ (схема 9)

Таблица 1 – Параметры структурной схемы линейной САУ

№ варианта	Параметры
17	0.15	15	3.3	5	4.58	0.003	0.56	0.036	0.04	0.03	0.01	0.2

Таблица 2 – Требования к качеству САУ

Номер варианта	Величина ошибки,	Время регулирования,	Максимальное перерегулирование,
25	0.0061	1.08	20

Для астатических САУ 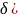–скоростная ошибка при скорости изменения входного сигнала

Допустимое количество колебаний не более 3

1. Анализ системы автоматического управления.

1A. Исследование заданной системы на устойчивость двумя критериями.

Исходную схему представим в следующем виде:

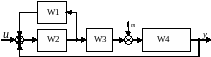
Рисунок 2 – Приведенная схема САУ

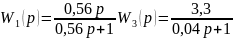
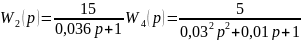
Найдем передаточную функцию

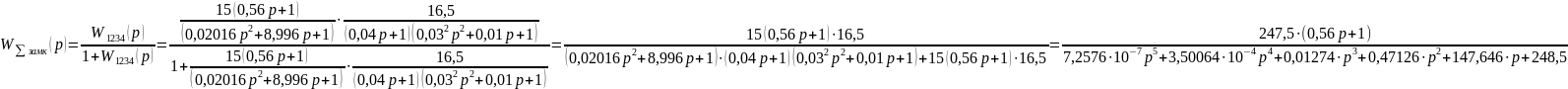
Сразу же определим передаточную функцию для случая разомкнутой системы:

Для анализа устойчивости САУ воспользуемся двумя методами: критерием Михайлова и критерием Найквиста.

Проверка устойчивости линейной САУ с помощью критерия Михайлова.

Для устойчивости линейной системы n-го порядка необходимо и достаточно, чтобы годограф Михайлова при изменении ω от 0 до ∞ начинался на положительной вещественной полуоси и проходил последовательно против часовой стрелки n квадрантов, не обращаясь в 0 и стремясь к ∞ в n-м квадранте. Расчет произведем в пакете Mathcad.

Рисунок 3 – Годограф Михайлова при w=0..1000

Таким образом, система согласно критерию Михайлова не устойчива.

Проверка устойчивости линейной САУ с помощью критерия Найквиста.

Если разомкнутая система устойчива (в нашем случае она устойчива согласно общему условию устойчивости: корни характеристического уравнения имеют отрицательную вещественную часть), то для устойчивости замкнутой системы необходимо и достаточно, чтобы на всех частотах, где ЛАЧХ разомкнутой системы положительна, фазовый сдвиг не достигал значения или достигал его четное число раз.

Рисунок 4 – ЛАЧХ разомкнутой системы

Рисунок 5 - ЛФЧХ разомкнутой системы

Исходя из рисунка 5, можно сделать вывод, что сдвиг по фазе достигает значения в -180 градусов при log(w)=1,56 дек. Вернемся к рисунку 4. При log(w)=1,56 значение функции положительно. Таким образом, система по критерию Найквеста неустойчива.

Так как система не устойчива, что подтвердилось анализами по двум критериям, то делать проверку на статическую ошибку не нужно.

2. Синтез системы автоматического управления

2А. Определение требуемого коэффициента передачи синтезируемой сау

Статическая ошибка не должна превышать максимально допустимую статическую ошибку:

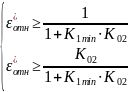
где 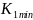– минимальный коэффициент усиления

Найдем коэффициенты усиления 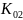и частей разомкнутой системы, находящихся после и до возмущаюшего воздействия соответственно.

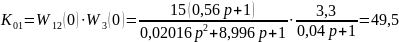
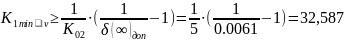
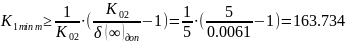
Выбираем большее значение. Таким образом,

Коэффициент усиления корректирующего устройства с учетом 10% запаса:

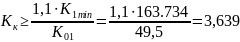
Принимаем: