1.6 Расчет вибрационной надежности облопачивания

Минимальная собственная частота единичной вращающейся лопатки с бандажом:

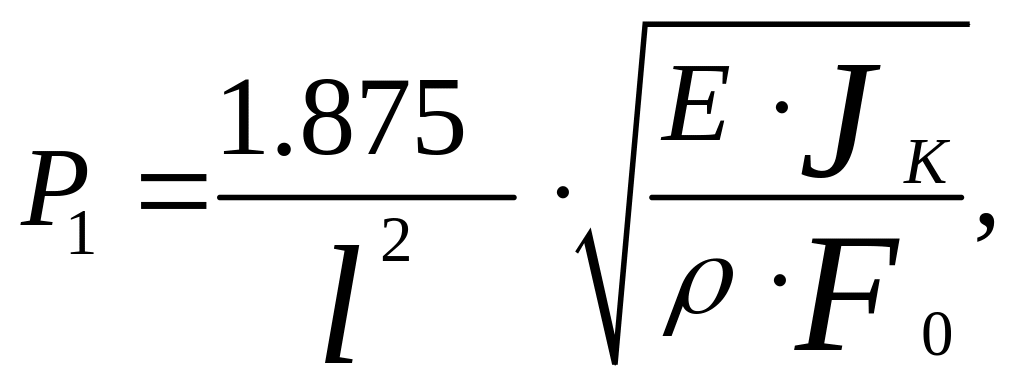
где плотность материала лопатки; - момент инерции сечения лопатки; F₀ =0,000244 м² - площадь поперечного сечения лопатки; - высота лопатки; модуль упругости, – число лопаток в пакете.

Тогда,

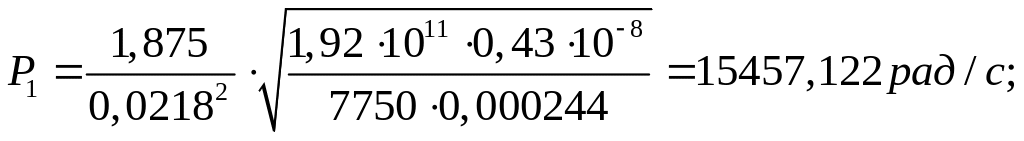
Собственная частота пакета лопаток:

Определим коэффициенты:

Гибкость лопатки:

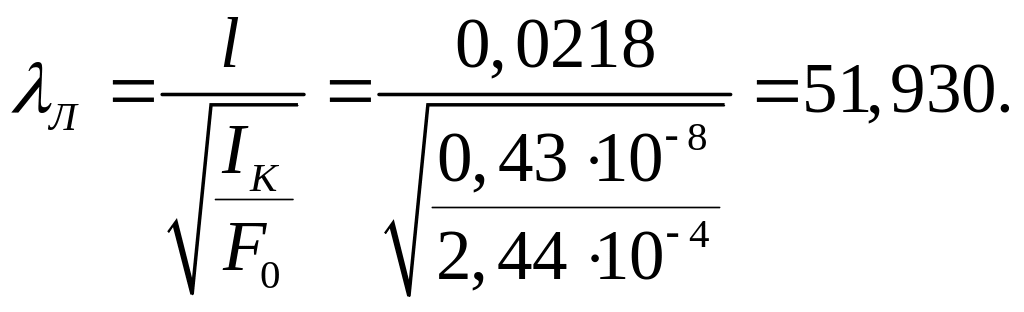
По рис. 5.11 [3] получаем

Определим влияние вращения на частоту колебаний по тону А₀.

Определим влияние вращения на частоту колебаний по тону .

Динамическая частота на расчетном режиме:

где .

Частота колебаний на расчетном режиме (в Гц):

Рис. 6. Диаграмма Кэмпбелла.

Абсциссы точек пересечения лучей кратности с кривой частоты f_д соответствуют резонансным числам оборотов.

_,

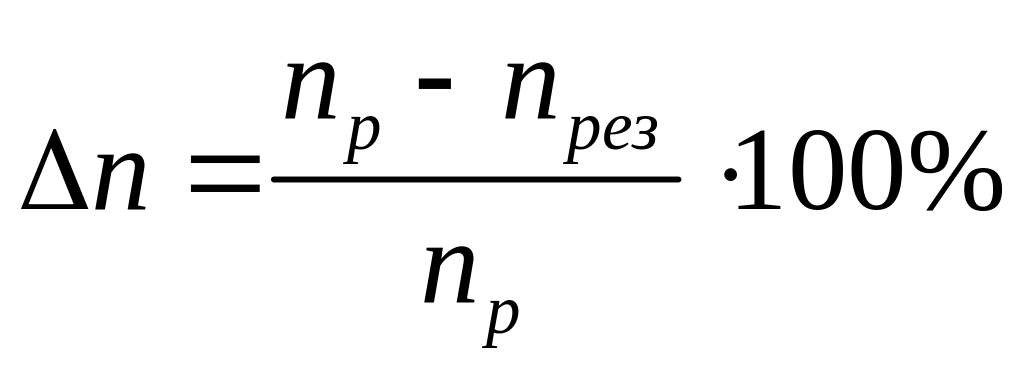где n_Р - рабочее число оборотов, n_рез – резонансное число оборотов, Δn составляет >10% для k=2, >7% для k=3, >6% для k=4, >5% для k=5, >4% для k=6, следовательно, лопатка вибронадежна.

3 Расчёт на прочность диска последней ступени

Исходные данные: n = 3000 об/мин, R =0,885 м, r_о = 0,110 м,

r₁= r_в = 0,1936 м, r₂ = 0,57 м, у₁= 0,113 м, у_в = 0,145 м, у₂ = 0,0487 м,

_r0 = -5 МПа. Материал: ст. 35ХМ ρ = 7750 кг/м³.

Рис. 8. Диск последней ступени

Центробежная нагрузка на внешнем радиусе полотна:

,

где С_Л – центробежная сила облопачивания;

С_об – центробежная сила обода диска;

k – коэффициент, учитывающий разгружающее действие обода, k=2/3 для Т –образных и грибовидных хвостовиков, k=1,0 – для дисков с осевой завязкой хвостовиков лопаток, а так же дисков последних ступеней, имеющих большие значения внешнего радиуса.

, где ; =1,36/0,173=7,861.

u_ср= π·d_ср·n/60 = π ·1,36·3000/60 = 213,628 м/с.

z = 109 шт.; F_к = 0,000122 м².

Материал лопаток: 20Х13 с плотностью ρ = 7750 кг/м³;

Центробежная сила обода диска:

где h = 0,08 м; b₁=0,065 м; r_об = 0,54 м.

Центробежная сила бандажа:

где

Тогда

1. Разбиваем втулку, полотно и обод диска на ряд сечений, включающих граничные радиусы:

для втулки: х = 0,11; 0,152; 0,1936;

для полотна: x = 0,1936; 0,265; 0,340; 0,415; 0,570,

где x – текущий радиус.

2. Определяем радиус полного конуса:

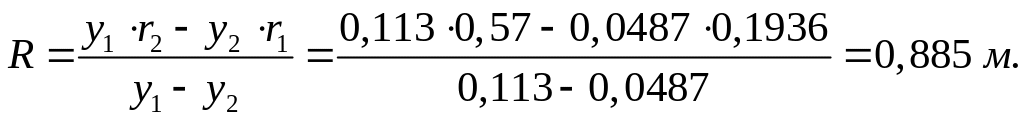
3. Для выбранных сечений определяем:

   1. для втулки – отношение x/r_o;

   2. для полотна диска – x/R.

По графикам [2, рис. 34, с. 56] и [2, рис. 39, с. 65] определяем:

-для втулки: К₁, К₂, К₃, К′₁, К′₂, К′₃;

-для полотна p_с, p₁, p₂, q_c, q₁, q₂;

Результаты приведены в таблице 3.

4. Определяем напряжения в тонких вращающихся кольцах радиусов r_o ,R:

;

Определим методом двух расчётов напряжения в диске.

I расчёт.

Исходные данные:

об/мин;

МПа (действительное);

МПа – принимаем произвольно.

Результаты первого расчёта приведены в таблице 4.

Расчётные зависимости для втулки:

Расчётные зависимости для полотна диска:

Найдём постоянные интегрирования А^I и В^I. Запишем уравнения для расчёта напряжений на радиусе r₁ конического диска.

;

.

Значения и находим по уравнениям перехода от ступицы к полотну:

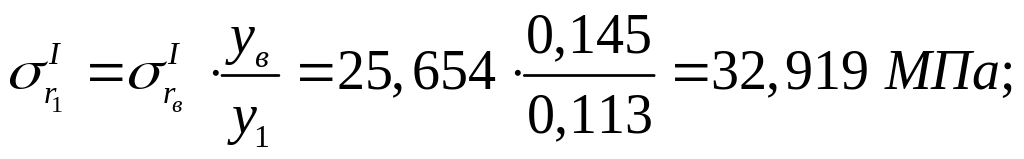
32,919 = 97,772+А^I·1,7+В^I·(-14,3);

57,657 =94,420+А^I·1,58+В^I·23,2;

Получаем значения постоянных интегрирования:

А^I=-32,729; В^I=0,644.