
Тема к зачёту
.doc
2. ЧАСТИЧНО УПОРЯДОЧЕННЫЕ
МНОЖЕСТВА И РЕШЕТКИ
Семантика рекурсивных программ использует понятия и результаты теории частично упорядоченных множеств.
Определение.
Частично
упорядоченным множеством
(ч.у.м.) называется множество А
вместе
с бинарным отношением
![]() ,
удовлетворяющим условиям:
,
удовлетворяющим условиям:
(рефлексивность):
х![]() х
х
(антисимметричность):
х![]() у,
у
у,
у![]() х
х
![]() х=у
х=у
(транзитивность):
x![]() y,
y
y,
y![]() z
z
![]() x
x![]() z
z
для
всех x,y,z![]() A.
A.
Определение.
Пусть
А
– ч.у.м. и
Х![]() А.
Элемент с
А.
Элемент с![]() А
(d
А
(d![]() A)
называется верхней
(нижней)
гранью для Х,
если х
A)
называется верхней
(нижней)
гранью для Х,
если х![]() с
(x
с
(x![]() d)
для всех х
d)
для всех х![]() Х.
Х.
Если
верхняя грань с
(нижняя
грань d)
принадлежит Х,
то с
(соответственно
d)
называется наибольшим
(наименьшим)
элементом для Х.
Очевидно,
что наибольший (наименьший) единствен:
если x≤c
и
x≤d
для
всех
х![]() Х,
то d≤c
и
c≤d
и, значит, c
= d.
Для
обозначения наибольшего и наименьшего
элементов множества Х
используются обозначения:
Х,
то d≤c
и
c≤d
и, значит, c
= d.
Для
обозначения наибольшего и наименьшего
элементов множества Х
используются обозначения:
с = max X и d = min X.
Наименьший и наибольший элементы ч.у.м. (А,≤) обозначаются T и ┴ .
Определения.
Пусть
Х![]() А.
Рассмотрим
множества
А.
Рассмотрим
множества
Y = {y | y – верхняя грань для Х },
Z = {z | z – нижняя грань для Х }.
Если множество Y (множество Z) имеет наименьший (наибольший) элемент, то этот элемент называется супремумом (инфимумом) для Х и обозначается sup X (соответственно, inf X). Таким образом,
sup X = min Y = min{y | y – верхняя грань для Х },
inf X = max Z = max{z | z – нижняя грань для Х }.
Элементы sup X и inf X называются, соответственно, наименьшей верхней гранью и наибольшей верхней гранью для Х.
Очевидно, что справедливы соотношения:
sup{a} = a, inf{a} = a;
sup{a,b}
= b
и
inf{a,b}
= a,
если
a![]() b.
b.
Вместо
sup{а,b}
и inf{a,b}
можно также писать a![]() b
и
a
b
и
a![]() b.
b.
Утверждение 1. Если существуют sup{a,b}, sup{b,c}, sup{a,b,c}, то
sup{a, sup{b,c}} = sup{sup{a,b},c}} = sup{a,b,c},
inf{a, sup{b,c}} = inf{inf{a,b},c}}} = inf{a,b,c}.
Другими словами, операции sup{x,y} inf{x,y} ассоциативны.
Доказательство.
sup{a,b,c}
= sup{{a}![]() {b,c}}
= sup{sup{a},
sup{b,c}}
{b,c}}
= sup{sup{a},
sup{b,c}}
= sup{a, sup{b,c}}.
sup{a,b,c}
= sup({a,b}![]() {c}}
= sup{sup{a,b},
sup{c}}
{c}}
= sup{sup{a,b},
sup{c}}
= sup{sup{a,b},c}.
Двойственным образом получаем соотношения для инфимумов.
Ч.т.д.
Для
супремума и инфимума двух элементов
используются также обозначения: a![]() b
= T и
┴ .
b
= T и
┴ .
Определения.
Ч.у.м.
А называется
решеткой,
если каждые два его элемента имеют
супремум и инфимум: a![]() b,
a
b,
a![]() b
ϵ
А.
Решетка называется ограниченной,
если
она имеет наименьший ┴
и
наибольший T
элементы.
b
ϵ
А.
Решетка называется ограниченной,
если
она имеет наименьший ┴
и
наибольший T
элементы.
Легко видеть, что ограниченную решетку можно определить как ч.у.м., для которого каждое конечное множество его элементов имеет супремум и инфимум. В самом деле, T = sup A и ┴ = inf A.
Определения.
Ч.у.м.
А
называется
полной
решеткой,
если для каждого его подмножества Х![]() А
существуют sup
X
и
inf
X.
(Таким
образом, полная решетка всегда ограничена.)
А
существуют sup
X
и
inf
X.
(Таким
образом, полная решетка всегда ограничена.)
Определения. Ч.у.м. А называется верхней (нижней) полурешеткой, если для любых двух его элементов a и b существует супремум sup{a,b} (соответственно, инфимум inf{a,b}). Если это верно не только двух элементов, но и для произвольного подмножества, то решетка, то полурешетка А называется полной.
Замечание. Ясно, что
inf
![]() = max{y
= max{y![]() A
|
y
– верхняя
грань для
A
|
y
– верхняя
грань для
![]() }
}
=
max{y![]() A
|
(
A
|
(![]() x
x![]() A)(x
A)(x![]()
![]()
![]() x
x![]() y)}
y)}
=
max{y![]() A
|
(
A
|
(![]() x
x![]() A)x
A)x![]() y}
= max
A.
y}
= max
A.
=
max{y![]() A
|
y
= max
А}
= max
A = T.
A
|
y
= max
А}
= max
A = T.
Двойственным
образом, sup
![]() = min
А
= ┴ .
= min
А
= ┴ .
Понятие решетки можно также определить с помощью алгебраических терминов.
Определение.
Решеткой
называют алгебру <A;
![]() ,
,
![]() >
с двумя бинарными операциями,
удовлетворяющими соотношениям:
>
с двумя бинарными операциями,
удовлетворяющими соотношениям:
(идемпотентность):
x![]() x
= x
и
x
x
= x
и
x![]() x
=x,
x
=x,
(коммутативность):
х![]() у
= у
у
= у![]() х
и
х
х
и
х![]() у
= у
у
= у![]() х,
х,
(ассоциативность):
(x![]() y)
y)![]() z
= x
z
= x![]() (y
(y![]() z)
и
(x
z)
и
(x![]() y)
y)![]() z
= x
z
= x![]() (y
(y![]() z),
z),
(поглощение):
х![]() (х
(х![]() у)
= х и
х
у)
= х и
х![]() (х
(х![]() у)
= х.
у)
= х.
Утверждение 3. Определения решетки как ч.у.м. и как алгебраической структуры эквивалентны.
Доказательство.
А)
Первое определение
![]() Второе определение.
Второе определение.
Идемпотентность
и коммутативность очевидны. Ассоциативность
была уже доказана. Поглощение следует
из того, что x![]() y
y
![]() x
и
x
x
и
x![]() x
x![]() y.
y.
Б)
Второе определение
![]() Первое определение.
Первое определение.
Отношение
порядка в множестве А
можно
определить двумя способами: x![]() y
df
x
y
df
x![]() y
= y
или
x
y
= y
или
x![]() y
df
x
y
df
x![]() y
= х. На
самом деле мы получаем одно и то же
отношение порядка, так как
y
= х. На
самом деле мы получаем одно и то же
отношение порядка, так как
x![]() y
= y
x
y
= y
x![]() y
= х.
y
= х.
В самом деле,
x![]() y
= y
y
= y
![]() х
х![]() (х
(х![]() у)
= х
у)
= х![]() у
у
![]() (поглощение) х
= х
(поглощение) х
= х![]() у,
у,
x![]() y
= х
y
= х
![]() у
у![]() (х
(х![]() у)
= у
у)
= у![]() х
х
![]() (поглощение) у
= х
(поглощение) у
= х![]() у,
у,
Докажем,
что отношение
![]() действительно является порядком, т.е.
оно рефлексивно, антисимметрично и
транзитивно.
действительно является порядком, т.е.
оно рефлексивно, антисимметрично и
транзитивно.
Рефлексивность:
х![]() х,
так
как х
х,
так
как х![]() х
= х
х
= х
Антисимметричность:
х![]() у,
у
у,
у![]() х
х
![]() х
х![]() у
= у, у
у
= у, у![]() х
= х
х
= х
![]() (коммутативность) у
= х.
(коммутативность) у
= х.
Транзитивность:
x![]() y,
y
y,
y![]() z
z
![]() x
x![]() y
= y,
y
y
= y,
y![]() z
= z
z
= z
![]() (x
(x![]() y)
y)![]() z
= z
z
= z
![]() (ассоциативность) x
(ассоциативность) x![]() (y
(y![]() z)
= z
z)
= z
![]() x
x![]() z
= z
z
= z
![]() x
x![]() z
z
Докажем
теперь, что sup{x,y}
= x![]() y.
y.
х![]() sup{x,y},
у
sup{x,y},
у![]() sup{x,y}
sup{x,y}
![]() х
х![]() sup{x,y}
=
sup{x,y},
у
sup{x,y}
=
sup{x,y},
у
![]() sup{x,y}
=
sup{x,y}
sup{x,y}
=
sup{x,y}
![]() (х
(х![]() sup{x,y})
sup{x,y})![]() (у
(у
![]() sup{x,y})
=
sup{x,y}
sup{x,y})
=
sup{x,y}![]() sup{x,y}
sup{x,y}
![]() (х
(х![]() y)
y)![]() sup{x,y}
=
sup{x,y}
sup{x,y}
=
sup{x,y}
![]() х
х![]() y
y![]() sup{x,y}.
sup{x,y}.
Таким
образом, х![]() y
y![]() sup{x,y}.
sup{x,y}.
x![]() (x
(x![]() y)
= x,
y
y)
= x,
y![]() (x
(x![]() y)
= y
y)
= y
![]() x
x![]() x
x![]() y,
y
y,
y![]() x
x![]() y
y
![]() sup{x,y}
sup{x,y}![]() x
x![]() y.
y.
Таким
образом, sup{x,y}![]() x
x![]() y.
Ч.т.д.
y.
Ч.т.д.
Утверждение
4. Если
А
и
В – решетки,
то их декартово произведение
А![]() В
также
является решеткой. Если А
и
В
– полные
решетки, то А
В
также
является решеткой. Если А
и
В
– полные
решетки, то А![]() В
–
полная решетка.
В
–
полная решетка.
Доказательство.
Если А
и
В
– решетки
в смысле первого определения (т.е.
рассматриваемые как ч.у.м.), то декартово
произведение решеток есть множество
А![]() В
с
порядком
В
с
порядком
(х,у)
![]() (х’,y’)
(х’,y’)
![]() df
x
df
x![]() x’
и
y
x’
и
y![]() y’.
y’.
Пусть
Х
– произвольное
подмножество множества А![]() В.
Положим
X1
= {x
В.
Положим
X1
= {x![]() A
|
(
A
|
(![]() y)
(x,y)
y)
(x,y)![]() X}
и
X2
= {у
X}
и
X2
= {у![]() A
|
(
A
|
(![]() х)
(x,y)
х)
(x,y)![]() X}.
Ясно, что для любого элемента
с = (a,b)
X}.
Ясно, что для любого элемента
с = (a,b)![]() А
А![]() В
имеет
место:
В
имеет
место:
с
– верхняя
грань для Х
![]() a
– верхняя
грань для
X1
и
a
– верхняя
грань для
X1
и
b – верхняя грань для X2.
Отсюда
следует, что sup
X
= (sup
X1)![]() (sup
X1).
Аналогично имеем inf
X
= (inf
X1)
(sup
X1).
Аналогично имеем inf
X
= (inf
X1)![]() (inf
X1).
(inf
X1).
Если
для решетки взять второе определения
(т.е. рассматривать ее как алгебру), то
в декартовом произведении
А![]() В
определяем
В
определяем
(х,у)![]() (х’,y’)
=df
(х
(х’,y’)
=df
(х![]() х’,
у
х’,
у![]() y’)
и (х,у)
y’)
и (х,у)![]() (х’,y’)
=df
(х
(х’,y’)
=df
(х![]() х’,
у
х’,
у![]() y’).
y’).
Эти два определения декартова произведения эквивалентны, так как (ввиду независимости компонент пары) имеет место:
(х,у)
![]() (х’,y’)
(х’,y’)
![]() (х,у)
(х,у)![]() [(х,у)
[(х,у)![]() (х’,y’)]
= (х,у)
(х’,y’)]
= (х,у)
![]() (х,у)
(х,у)![]() [(х,у)
[(х,у)![]() (х’,y’)]
= (х,у)
(х’,y’)]
= (х,у)
Ясно,
что (ввиду независимости компонент
пары) в алгебре <А![]() В;
В;![]() ,
,
![]() >
для операций
>
для операций
![]() и
и
![]() выполняются соотношения идемпотентности,
коммутативности, ассоциативности и
поглощения. Поэтому эта алгебра является
решеткой. Ч.т.д.
выполняются соотношения идемпотентности,
коммутативности, ассоциативности и
поглощения. Поэтому эта алгебра является
решеткой. Ч.т.д.
Пример.
Рассмотрим
тривиальную решетку В,
состоящую из двух элементов ┴
и
T
с отношение порядка ┴
<
T.
Диаграммы Хассе для декартовых степеней
В2
= В![]() В
и В4
= В2
В
и В4
= В2![]() В2
показаны на рис.5.
TT
В2
показаны на рис.5.
TT



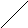 В2
┴T
T┴
В2
┴T
T┴
┴┴
TT




aT Ta Tb b T












В4 aa ab ┴T T┴ ba bb










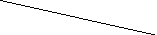



 a┴
┴a
b┴
┴b
a┴
┴a
b┴
┴b

┴┴
Рис.5
Определение.
Пусть
А
и
В
– ч.у.м.
Функция f
: A![]() B
называется монотонной,
если для любых х,
у
B
называется монотонной,
если для любых х,
у![]() А.
А.
x![]() y
y
![]() f(x)
f(x)![]() f(y).
f(y).
Примеры: 1) В множестве N = {0,1,2,…} зададим порядок:
х![]() у
у
![]() df
х
– делитель
у.
df
х
– делитель
у.
Функция f(x) = 2x является монотонной:
х![]() у
у
![]() х – делитель
у
х – делитель
у
![]() 2х
– делитель
2у
2х
– делитель
2у
![]() 2х
2х![]() 2у.
2у.
Функция
g(x)
= x+2
не является монотонной: 3![]() 9,
но не верно, что 3+2
9,
но не верно, что 3+2![]() 9+1.
9+1.
Функция
h(x,y)
= xy,
h
:
N2
![]() N,
является монотонной:
N,
является монотонной:
(x,x’)![]() (y,y’)
(y,y’)
![]() x
x![]() y,
x’
y,
x’![]() y’
y’
![]() x
– делитель
y,
x’
– делитель
y’
x
– делитель
y,
x’
– делитель
y’
![]()
xy
– делитель
x’y’
![]() ху
ху
![]() x’y’,
т.е.
h(x,y)
x’y’,
т.е.
h(x,y)![]() h(x’,y’).
h(x’,y’).
2)
Пусть A
– произвольное
множество и P(A)
= {X
| X![]() A}
– множество всех подмножеств множества
А.
В
P(A)
имеется естественный порядок –
теоретико-множественное включение.
A}
– множество всех подмножеств множества
А.
В
P(A)
имеется естественный порядок –
теоретико-множественное включение.
Функция
f
(X,Y)
= X![]() Y,
f
:
P(A)
Y,
f
:
P(A)![]() P(A)
P(A)
![]() P(A)
монотонна:
P(A)
монотонна:
