Тема 2:«Основы гидростатики»

Задача 3. Определить показание мановакууммет-ра , если к штоку поршня приложена сила F =0,5 кН, его диаметр d = 78 мм, высота H= 1,5 м, плотность жидкости = 800 .

Решение:

Гидростатическое давление в точке С (сверху) под слоем жидкости можно определить, используя закон Паскаля: Р_с= Р₀+ gH. Давление в воздухе над поверхностью жидкости Р₀ = Р_атм+ Р_мв.Давление справа, со стороны поршня Р_с=Р_атм+ . Давление в жидкости в любой её точке одинаково со всех сторон.

Рис. 2 к задаче 3.

Следовательно:Р₀+ gH= Р_атм+ . Р_атм+ Р_мв + gH = Р_атм+ .

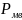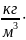Отсюда находим Р_мв= - gH. = –800 9,8

=1,05 10⁵Па – 0,12 10⁵Па =0,93 10⁵Па = 93 кПа.

Ответ: показания мановакуумметра Р_мв= 93 кПа.

Задача 4.Определить манометрическое давление в центре трубопровода (точка А), если высота столба ртути по пьезометру h₂ = 0,30 м. Центр трубопровода расположен на h₁ = 0,5 м ниже линии раздела между водой и ртутью.

Решение:

Находим давление в точке В. Точка В расположена выше точки А на величину h_1. Давление в точках В, С и D будут одина-ковы (в одной и той же жидкости на одинаковой высоте значения давлений одинаковы). Абсолютное давление в точке D (а, следо-вательно, и точке В) равно сумме давления столба ртути высотой h₂ и атмосферного давления Р_атм. Абсолютное давление в точке А равно сумме давления в точке В и давления столба воды высотой h₁. Следовательно: Р_А= ρ_в gh₁ + Р_атм + ρ_рт gh₂ ; Манометрическое

Рис.3к задаче 4.

давление (в данном случае это избыточное давление) равно раз-ности абсолютного и атмосферного давлений. Следовательно Р_А^м= (10³ •0,5 м + 13,6 • 10³ •0,30 м) •9,8 = 44,9•10³Па.

Ответ: манометрическое (избыточное) давление в центре трубы Р_А^м= 44,9 кПа.

Тема 3: «Основы гидродинамики»

Задача 5. Разность пьезометрических напоров в сече-ниях 1-1 и 2-2 равна 30 см. Определить коэффициент линей-ных потерь на участке между сечениями 1 и 2, если длина участка трубы L = 1 м, диаметр трубы d= 20 мм, а расход жид-кости, протекающей по трубе Q =0,54 .

Решение:

Запишем уравнение Бернулли в общем виде для потока реальной жидкости:

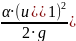[ + + ]- [ + + ] = h_1-2

Рис. 4 к задаче 5.

Коэффициенты Кориолиса можно взять равными 1, так как о них в условиях задачи нет сведений. Определить их, используя число Рейнольдса, так же нельзя, так как не указана жидкость и нет данных по её плотности и вязкости. Условно принимаем движение жидкости турбулентным, что чаще всего и бывает на практике. Для такого вида движения коэффициенты Кориолиса равны 1. При равенстве диаметров сечений 1 и 2 средние скорости движения жидкости и скоростные напоры одинаковы. Их разность равна нулю. По определению, геометрические напоры также одинаковы. Их разность тоже равна нулю. С учётом сказанного уравнение Бернулли принимает вид:

(H_п1 - H_п2 ) = h_1-2

Важный вывод: в горизонтальных трубах постоянного диаметра полные потери напора численно равны разности пьезометрических напоров в выбранных сечениях 1-1 и 2-2.

Так как на данном участке трубы местные сопротивления отсутствуют, полные потери равны линейным потерям напора. Согласно формуле Дарси:

h_л= λ_тр · ( ) · Следовательно, в данном случае (H_п1 - H_п2 ) = λ_тр · ( ) · ( ) . Отсюда находим коэффициент линейных потерь:

λ_тр = .

Скорость движения жидкости в трубе находим через расход жидкости:

U = ;S = = = 3,14 ·10^-4 м²

Подставляем значения и находим скорость:

U = = 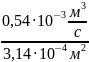= 1,72 .

Находим коэффициент линейных потерь:

λ_тр = = = 0,04.

Ответ: коэффициент линейных потерь на участке трубы составляет λ = 0,04.

Задача 6. В горизонтально расположенной трубе диа-метром 6,0 см на расстоянии L = 10 м друг от друга располо-жены два манометра, между которыми находится кран, име-ющий коэффициент местного сопротивления ε =2,7. Опреде-лить коэффициент линейных потерь на участке между сече-ниями 1 и 2, если разность показаний манометров равна 2,16 кПа, а расход жидкости в трубе составляетQ= 2 . Жидкость – вода, при 20⁰С (плотность ρ = 10³ , а динамическая вяз-кость η=10^-3 Па с.

Рис.5 к задаче 6.

Решение:

Запишем уравнение Бернулли в общем виде для потока реальной жидкости:

[ + + ]- [ + + ] = h_1-2

Коэффициенты Кoриолиса определим, рассчитывая чис-ло Рейнольдса. При Re>4000 (режим течения турбулентный) коэффициент Кориолиса равен 1, а при Re< 2300 (режим течения ламинарный) коэффициент Кориолиса равен 2. Находим число Рейнольдса: Re = . Скорость течения воды:

U= = 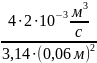= = 0,71 .

Re = = = 42600. Режим турбулентный, α = 1. При равенстве диаметров сечений 1 и 2 средние скорости движения жидкости и скоростные напоры оди-наковы. Их разность равна нулю. По определению, геометричес-кие напоры также одинаковы. Их разность также равна нулю. С учетом сказанного, уравнение Бернулли принимает вид: = . Согласно Дарси: = λ · ( ) · ; ; Следовательно, в данном случае:

= λ · ( ) · + . Отсюда находим коэффициент линейных потерь:

(Р₁-Р₂)= ρ [λ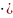 ( ) + ]; λ ) + = ;

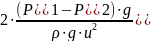λ ) = - ;λ= = ; ) =

λ = = 0,035.

Примечание: если в условиях задачи задана разность пье-зометрических напоров Н (м), то коэффициент гидравлического трения удобнее рассчитывать как:

λ_тр =

Ответ: коэффициент линейных потерь на участке трубы между сечениями 1 и 2 составляет λ = 0,035.

Задача 7. По трубе диаметром 5,06 см течёт вода со скоростью U= 1 . Принимая плотность жидкости равной

ρ = 1 , а динамическую вязкость η = 0,001 Па·с, определить число Рейнольдса, а затем коэффициент линейных потерь.

Решение:

Число Рейнольдса определяется следующим образом: Re = Re_d = ;

Re= = 5,06 ·10 ⁴ Получим размерность числа Рейнольдса:

Па с = = = ;

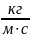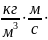м = ;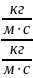 = 1. Число Рейнольдса не имеет размерности (безразмерное число).

Число Рейнольдса оказалось больше критического. Для нахождения коэффициента Дарси (коэффициента линейных потерь) в интервале 4000 <Re< 10⁵ используем формулу Блазиуса:

λ_тр = 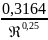= = = 0,02.

Ответ: Re = 5,06 ·10 ⁴ ; λ = 0,02.