Математические методы в лингвистике

Введение

Применение математических методов

грамматические и семантические признаки текста

звуко-буквенные ассоциации

модели стихотворного ритма и рифмы

тематическая структура ХТ

динамика индивидуального стиля

структура литературной ситуации

… …

В. Г. Адмони, В. С. Баевский, М. Л. Гаспаров, А. П. Журавлев, Ю. Н. Караулов, А. Н. Колмогоров, А. Я. Шайкевич, J. F. Burrows, T. N. Corns, D. L. Hoover и многие др.

Направления и темы курса

Основы математического анализа в лингвистике.

Статистическая лексикография. Статистика и корпусная лингвистика.

Математические методы в стилистике и лингвистике текста. Стилометрия. Статистика и фоносемантика.

Статистические меры при оценке степени близости слов. Измерение семантических расстояний.

Критерии социолингвистического и ассоциативного эксперимента.

Вопросы кодификации нормы и количественные исследования речевой вариативности.

математические методы в общем языкознании: классификация языков, глоттохронология, исследование циклических процессов в языке и т. д.

Специфика гуманитарных исследований

Неточность, расплывчатость понятий и определений. Многозначность терминологии.

Преобладание качественных характеристик их основных объектов.

Ограниченность возможностей проведения активного эксперимента.

Большой объем исходной информации.

Именно второй пункт, преобладание качественных (а не количественных) характеристик объектов, осложняет построение формализованных теорий в гуманитарных сферах.

Острота четвертого пункта в отношении текстового анализа постепенно снимается с развитием компьютерных систем и корпусных проектов.

Лингвистика

Гуманитарная сфера?

1. Особенности лингвистических объектов

2. Общие интересы наук:

лингвистика  биология, физика

лингвистика  социология, психология

лингвистика  математика, информатика

… … …

? лингвистика  литературоведение

Свойства лингвистических объектов

измеримость

системность

вероятностный характер процессов

Случайным (стохастическим) называется процесс, мгновенные значения которого являются случайными величинами.

Детерминированные процессы: уникальный и предопределённый результат для заданных входных данных.

Компьютерный алгоритм, химическая реакция.

Подвижность языковой системы, существование «исключений».

Вообще, все процессы, имеющие развитие во времени, с точки зрения теории вероятностей, можно называть стохастическими.

Асимметричность языкового знака

Соотношение формы и содержания:

полисемия

синонимия

Языковые vs. математические знаки

Естественные vs. искусственные языки

Генеральная проблема формализованного разрешения неоднозначностей (снятия омонимии)

Еще раз о формализации

Ю. Н. Марчук: любые данные о языке можно представить в лексикографической форме и — далее — перевести в алгоритмизованную, машинную форму.

[?]

По сути это постулат компьютерной лингвистики.

Еще раз о формализации

Особенности применения формальных методов на графико-фонетическом, словообразовательном, лексическом, синтаксическом, композиционно-текстовом уровнях.

Формальные показатели грамматических значений.

Идиоматичность семантики и затруднительность ее формализации и моделирования.

О разной степени формализации языка

Чем больше степень формализованности метода, тем лучше он будет работать при статистическом измерении. Сравним:

Буквы и буквосочетания

Грамматические признаки слов, синтаксические конструкции

Лексемы (служебные слова/местоимения/знаменат. лексика

Элементы композиции

Слово как центральная единица языка, лексическая статистика

Статусы слова:

лексема – лемма

словоформа – текстоформа (самое частное понятие; термин часто употребляется в корпусной лингвистике). Самое формальное определение т.: «набор знаков от от пробела до пробела»

*слово-ономатема – слово-синтагма в классической лексикологии

Новый частотный словарь русской лексики

Под ред. С. А. Шарова и О. Н. Ляшевской

http://dict.ruslang.ru/freq.php

Основан на данных Национального корпуса русского языка

Содержит информацию о частоте лексем и словоформ разных частей речи

+

Встречаемость слов в текстах разных функц. стилей

Данные о частотности частеречных классов

Частотность букв русского алфавита

Частотность двубуквенных сочетаний

Частотность имен собственных и аббревиатур

Лингвистическая теория текста

Текст – самый сложный лингвистический объект.

Устная речь и художественные тексты как самые сложные тексты.

Стремление к системному описанию формальных и смысловых характеристик (художественного) текста:

см. работы Л. Г. Бабенко, Н. С. Болотновой, В. Г. Гака, И. Р. Гальперина, Ю. В. Казарина, В. А. Лукина, Л. А. Новикова, В. А. Пищальниковой, И. Я. Чернухиной и др.

Опять о «гуманитарности»

Даже упомянутые структурные модели не являются настолько строгими, чтобы их можно было бы превратить в компьютерные алгоритмы.

Моделирование макрокатегорий — таких, как образы автора и персонажей, художественное пространство и время и др., —предполагает человеческое прочтение.

Специфика восприятия литературного произведения, помимо интерпретации смысла слов, предполагает не что иное, как переживание текста читателем.

Формализация при АОТ

Практика автоматической обработки текста — в том числе информационный поиск, автоматическое аннотирование, машинный перевод и т.п. — выдвигает особые требования к «интегральному» описанию текста, которое должно быть абсолютно лишено неформализованных блоков информации, интуитивно понятных только человеку.

Аксиоматические положения

математические методы, позволяют свести до минимума субъективизм исследователя, количественно оценить результат и проверить степень его достоверности.

Чем больше по объему материал, тем объективнее результаты исследования. (вопрос повторяемости единиц).

Необходимо учитывать степень формализации лингвистического материала.

Количественное исследование становится по-настоящему объективным, если оно имеет сравнительный характер.

Корректность выборки зависит от набора причин (пространство, время, человек etc.).

There are three kinds of lies: lies, damned lies, and statistics

Объективность vs. корректность модели

Мат. методы (в том числе математическая статистика) – это лишь инструмент для работы. Представления и гипотезы о причинной связи должны быть привнесены из некоторой другой теории, которая позволяет содержательно объяснить изучаемое явление.

Иными словами, даже верные статистические показатели могут создать картину, которая противоречит языковой (тем более – литературно-художественной) действительности.

Cтатистические инструменты в применении к лингвистическим объектам

Статистика

(от латинского status)

Отрасль знаний, изучающая количественную сторону массовых явлений в числовой форме.

Выявляет скрытые закономерности и изучает их с помощью обобщенных показателей.

Статистика и лингвистика: эффективность взаимодействия

Гармоничное сочетание качественных (традиционных и во многом – интуитивных) и количественных методов.

Понимание типов лингвистических задач, решаемых статистическими методами, и возможной исчислимости яз. единиц и их признаков.

Знание лингвистом необходимого набора статистических инструментов.

Текст, словарь, корпус

Основными объектами применения статистики в языкознании обычно является речь (текст), словарные и грамматические данные.

Текст → язык. Количественное описание функционирования различных языковых единиц (фонем, букв, морфем, слов) в тексте: частота употребления единиц, их распределение в текстах разного жанра, сочетаемость и т. п.

Накопление количественной информации о классах единиц, о конструкциях (напр., данные о средней длине слова или предложения, о частоте употребления каких-либо грам. форм в тех или иных синтаксических функциях и т. п.).

Такая информация углубляет описание единиц языка.

Сегодня объектом применения статистики все чаще становятся лингвистические корпуса.

Выборочный метод в статистике

Статистический метод исследования общих свойств совокупности каких-либо объектов на основе изучения свойств лишь части этих объектов, взятых на выборку.

Необходим, когда исследовать всю совокупность (например, по причине объема) невозможно. [Пример с кубиком]

В лингвистике используется широко:

исследование множественных речевых фактов

социолингвистические опросы (напр., критерии нормативности, лингвистические ассоциации, вопросы интерпретации текстов и т. д.)

Выборочный метод

Пример с орфоэпическим опросом:

обеспéчение или обеспечéние?

Случайная величина в этом случае может принимать только одно значение из двух (если только информант не колеблется).

Тогда возможные степени градации:

не знаю

скорее, 1-е

скорее, 2-е

Генеральная совокупность и выборка

Генеральная совокупность – множество всех мыслимых значений изучаемой величины.

Выборка – некоторое наблюдаемое подмножество генеральной совокупности.

проблемная область vs. корпус данных

корпус данных vs. конкорданс

Самый объемный поставщик генеральных совокупностей – вся речевая деятельность.

Требования к выборке

по выборке (т. е. по части множества) мы должны сформировать некое представление о всей генеральной совокупности. Чтобы оно не было ошибочным, к выборке предъявляются критерии

репрезентативности

однородности

Репрезентативность и однородность выборки

Репрезентативность: у каждого элемента генеральной совокупности равные шансы попасть в выборку.

Однородность: в выборке представлены значения одной случайной величины, а не нескольких, имеющих существенно различные распределения.

[расчет средней зарплаты]

[распределение слов, напрямую связанных с сюжетом текста]

Первичная обработка данных: пробы и выборочные частоты

Частота как число повторений или возникновений событий (фактов, процессов). Частоту лингвистических явлений или единиц, как правило, нельзя точно предсказать до её измерения. Следовательно, она случайная величина.

Генеральная совокупность → пробы (выборки опред. объема) → суждения о частотах. Выборочные частоты – частоты, показанные отдельными выборками.

Формулы: обозначения частот

Выборочные частоты: x₁, x₂, x₃, x₄… x_n

Любая выборочная частота: x_i

Средняя частота: x.

Первичная обработка данных: группировка

Элементы, наблюдавшиеся в выборке располагаются в порядке возрастания (убывания) соответствующих им частот (для дискретных случайных величин).

! Случайная величина называется дискретной, если ее множество значений конечно или счетно, т. е. значения можно пронумеровать натуральными числами.

Дискретные и непрерывные величины

Примеры непрерывных величин:

масса тела человека за десять лет жизни

скорость автомобиля в течение часа

Выборка и группировка: дискретизация непрерывных величин

Лингво-статистические показатели, как правило, дискретны:

Частота слова в тексте

Количество грамматических разрядов в языке

Количество говорящих

* Количество значений в словаре vs. количество актуальных смыслов слова в речи (проблема синкретизма значений).

Слово идея в толковом словаре

БТС (значения в словаре всегда дискретны):

1. Понятие, представление. Отвлеченная и. || Мысленный образ чего-л., понятие о чем-л. Идеи добра.

2. Прочно сложившееся мнение, уверенный взгляд на что-л. <…> Преданность идее, Политические идеи.

3. Мысль, замысел, намерение, план. И. возрождения России. Прекрасная и.

4. Основная мысль, определяющая содержание какого-л. произведения. || Основной принцип устройства чего-л. И. картины, поэмы.

5. В идеалистической философии: основная причина и источник исторического развития. Абсолютная и.

Слово идея в контексте: А. Платонов, «Чевенгур», смысловой синкретизм

Большевики и прочие уже разошлись с прежнего места, они снова начали трудиться над изделиями для тех товарищей, которых они чувствовали своей идеей.

Вас она [Софья Александровна] помнит — у вас в Чевенгуре люди друг для друга как идеи, я заметил, и вы для нее идея; от вас до нее все еще идет душевный покой, вы для нее действующая теплота…

Идея человека в этих случаях — это и понятие о нем, и мнение, и намерение сделать что-либо для него и себя. Речь здесь идет и об особом философском устройстве человека.

Группировка: лексические частоты в НЧС РЯ

Группировка данных в Access

Группировка данных в Access

Первичная обработка данных: графическое представление

Гистограмма: количественные соотношения показателя представлены в виде прямоугольников или др. фигур, размеры которых пропорциональны.

Первичная обработка данных: графическое представление

Графики делают данные наглядными.

Изучение графика часто позволяет обнаружить дефектность выборки или выдвинуть первичное предположение о распределении данных.

Дальнейшая обработка данных: точечные оценки распределения

Т. о. – число, вычисляемое на основе наблюдений, предположительно близкое к оцениваемому параметру.

Средние значения

Показатели разброса значений

Средние значения

Выборочное среднее – среднее арифметическое для элементов выборки.

Мода – значение, которое встречается наиболее часто. Распределение может иметь несколько мод.

Медиана – значение, которое делит ранжированную выборку на две равные части (или среднее по порядку, рангу значение). Медиана часто согласуется с интуитивным пониманием «среднего».

Средние значения

Выборочное среднее = 157 : 22 = 7,1363636

Мода = 8 (встречается 9 раз). Если в выборке более чем одна мода, она называется мультимодальной.

Медиана = 7 (средняя частота 11-го и 12-го элементов из 22)

В данном случае ср. знач. близки, но они могут существенно расходиться. Вопрос построения модели!

В крупном тексте: «Тихий Дон» (424 684 текстоформы, 22409 знаменатель-ных лемм)

«Тихий Дон»: для знаменательных лемм (22409)

Выборочное среднее = 11,6.

Мода = 1 (встречается 7480 раз). Обычный показатель для практически любого протяженного текста.

Медиана = 3 (частота элемента ранга 11205 из 22409).

Показательность/обманчивость средних величин

Мода и медиана могут быть гораздо более объективными показателями, чем выборочное среднее при выборке, не отвечающей критериям репрезентативности и однородности.

Показатели разброса значений

Объективация средних показателей: методика вычисления отклонения от средней частоты

Стандартные и распространенные показатели разброса значений:

дисперсия

среднее квадратическое отклонение

Эти показатели взаимосвязаны

Дисперсия (Variance, Var.)

 Мера разброса случайной величины, то есть её отклонения от среднего значения:

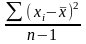
сумма возведенных в квадрат отклонений частот от среднего показателя, поделенная на n (число выборок) – 1.

Вычисление дисперсии

Допустим, частота слова война в 10 массивах текстах СМИ (ipm) колеблется след. образом:

1000, 970, 1010, 1100, 950, 1002, 980, 999, 1030, 1015

= 1005,6

соотв. 25,6, 1229,2, 24,4…

сумма квадратов отклонений = 14719,32

делим на 10 – 1 = 9

показатель дисперсии = 1635,48

! Дисперсия постоянной величины равна 0.

Среднее квадратическое (стандартное) отклонение (Standard Deviation, Std.Dev.), обозначается  или s

Наиболее распространённый показатель разброса значений. Используется при расчёте стандартной ошибки среднего арифметического в статистических измерениях. Определяется как квадратный корень из дисперсии.

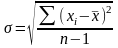
Вычисление СКО (дополнение к примеру со словом война)

Допустим, частота слова война в 10 массивах текстах СМИ (ipm) колеблется след. образом:

1000, 970, 1010, 1100, 950, 1002, 980, 999, 1030, 1015

= 1005,6

соотв. 25,6, 1229,2, 24,4…

сумма квадратов отклонений = 14719,32

показатель дисперсии = 1635,48

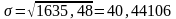
СКО:

Интерпретация СКО (дополнение к примеру со словом война)

Значения нормально распределённой случайной величины обычно лежат в интервале

(1005,6 – 121,32);(1005,6 + 121,32)

884,28 ~ 1126,92

1000, 970, 1010, 1100, 950, 1002, 980, 999, 1030, 1015

Практическая арифметика для гуманитариев (?)

На практике статистические функции встроены в различные приложения – не только в совсем специализированные (SPSS, Statistica, Statgraphics etc.), но и в универсальные: Access, Excel…

Поэтому главное для гуманитария не столько умение считать (хотя это важно ), сколько знание функциональности статистического инструментария. Это знание позволяет избежать вульгаризации статистики.

Примеры использования показателей разброса: НКРЯ, НЧС РЯ [Шаров, Ляшевская]

Выравнивание распределения частот в сегментах корпуса (коэф. Жуйана, D):

корпус разбивается на n сегментов (100), отражающих жанрово-стилевую разбивку

известны средняя частота слова по всему корпусу (μ) и  – среднее квадратическое отклонение μ для отдельных сегментов.

D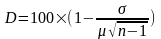 вычисляется по формуле:

Примеры использования показателей разброса в НКРЯ [Шаров, Ляшевская]

Значение D у слов, частотных в большинстве документов, близко к 100, а в небольшом количестве – к 0. Примеры:

союз но (встречается во всех сегментах): D = 97

сущ. статья (преобладает в юридич. документах): D = 76

сущ. конунг (встречается только в 9, преим. литературно-худож. сегментах): D = 9

Примеры использования показателей разброса при изучении стихотворного ритма [Коломогоров, Баевский]

Каждому слогу стиха ставится в соответствие мера выделенности m, где m принимает значение исходя из ударности/редуцированности (5 степеней градации).

Вычисляется средняя выделенность одного слога по стихотворению в целом.

Среднее квадратическое отклонение выделенности слогов отражает индивидуальные характеристики строки → строфы → текста → стиля → направления…

В.С.Баевский:

«Строки с наибольшим средним квадратическим отклонением суть ритмические раритеты. Они больше всего отличаются от идеального «усредненного» ритма, имеют наиболее заметный индивидуальный ритмический облик».

В итоге среднее квадратическое отклонение выделенности слогов строки «отражает процесс восприятия стиха как результат взаимодействия между ожидаемым вследствие предшествующего читательского опыта и индивидуальным ритмическим обликом данной строки».

В.С.Баевский:

«Стих Б. Пастернака, Н. Ушакова, Л. Мартынова, А. Прокофьева, Д. Самойлова, А. Вознесенского — поэтов разных поколений и разных творческих установок — отличается высокой изменчивостью ритма

Стиху позднего П. Антокольского, А. Твардовского, Я. Смелякова, Е. Винокурова, Е. Евтушенко — опять-таки поэтов очень разных — свойственно ограничение изменчивости ритма.

Первая установка носит новаторский характер, вторая ориентирована на традицию XIX в.».

Cтатистические инструменты в применении к лингвистическим объектам (продолжение)

Необходимость оценки вариативности частот

Случайны или существенны отклонения выборочных частот от средней?

Подчиняются ли общему статистическому закону колебания лексических частот, наблюдаемые на материале корпуса, или метрические отклонения в поэтических текстах?

Два направления ответов:

методы статистики

методы проблемной области (филологии)

Изучение распределения случайных величин

Пример: критерий Пирсона (χ²-критерий)

Распределение в статистике

Распределение вероятностей — закон, описывающий область значений случайной величины и вероятности их принятия.

Р. вероятностей какой-либо случайной величины, задаётся указанием возможных значений этой величины и соответствующих им вероятностей.

В статистике используются различные виды распределений.

Критерий Пирсона (χ²) Chi-squared distribution

(«Критерий согласия») Наиболее универсальный из всех используемых в статистике.

Оценка существенности расхождения наблюдаемых частот языкового явления.

Если выборки имеют одинаковую длину, то

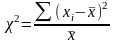
позволяет сличить наблюдаемые величины с теоретической (ожидаемой) величиной.

Критерий Пирсона (χ²)

Можно ли предполагать, что колебания частот случайны, т.е. подчиняются статистическому закону варьирования средней частоты?

Если нет, то они существенны, т. е. на них оказывают влияние внешние, не чисто статистические факторы.

Функция ХИ2ТЕСТ (CHISQ.TEST) в Excel.

Критерий Пирсона (χ²)

Пример Б.Н.Головина (учебник «Язык и статистика»): 5 выборок по 500 знаменательных слов.

Частоты имен прилагательных: