Тема 7. Гипотезы об «однородности». Однофакторный дисперсионный анализ.

1. Критерий однородности Колмогорова-Смирнова.

Пусть наблюдение состоит из двух независимых выборок: – выборка из распределения , – выборка из распределения , и независимы. Основная гипотеза заключается в том, что выборки и однородны (являются выборками из одного и того же распределения), то есть :

: .

Требуется составить критерий для проверки гипотезы .

Если функция является непрерывной, то для проверки гипотезы может использоваться критерий однородности Колмогорова-Смирнова, статистика которого имеет вид:

,

где – эмпирическая функция распределения выборки и – эмпирическая функция распределения выборки . Если гипотеза не верна, то есть , то функции эмпирического распределения и сходятся к различным функциям, поэтому точная верхняя грань модуля разности не стремится к нулю с увеличением , а стремится к конечному числу отличному от нуля, которое затем умножается на возрастающую величину . Отсюда следует, что в случае если гипотеза не верна статистика с большой вероятностью принимает «большие» значения, поэтому «большие» значения статистики свидетельствуют против гипотезы и в критическую область гипотезы следует отнести «большие» значения статистики :

,

где пороговое значение определяется из распределения статистики и заданного уровня значимости . При больших и распределение статистики может быть вычислено приближенно на основе теоремы Смирнова.

Теорема 7.1. (Смирнов)

Пусть и – независимые выборки из распределения , – функция эмпирического распределения выборки , – функция эмпирического распределения выборки и статистика :

.

Если – непрерывная функция, тогда для любого фиксированного :

.

Без доказательства.

Таким образом, если гипотеза верна, то при больших и для заданного уровня значимости получим приближенное равенство:

,

,

откуда численно определяется значение .

2. Критерий Фишера.

Пусть наблюдение образовано двумя независимыми выборками: – выборка из нормального распределения , – выборка из нормального распределения , и – независимы, параметры , , и – неизвестны. Основная гипотеза заключается в том, что :

: .

Требуется составить критерий проверки гипотезы .

Для проверки гипотезы используется критерий Фишера со статистикой:

, , , ,

(7.1)

Утверждение 7.2.

Пусть – выборка из нормального распределения , – выборка из нормального распределения , и – независимы. Основная гипотеза заключается в том, что .

Если гипотеза верна, тогда статистика (7.1) имеет распределение Фишера .

Доказательство:

Согласно теореме Фишера (теорема 5.5) случайная величина имеет распределение , а случайная величина имеет распределение , причем и независимы, поскольку выборки и независимы.

Если гипотеза верна, тогда :

,

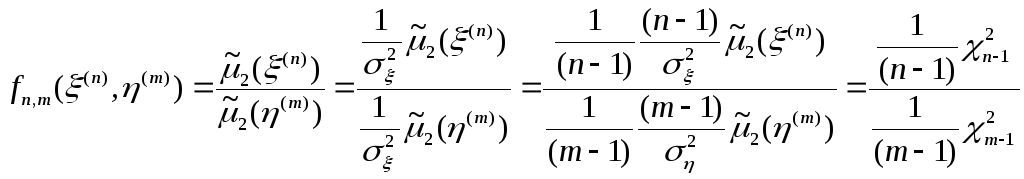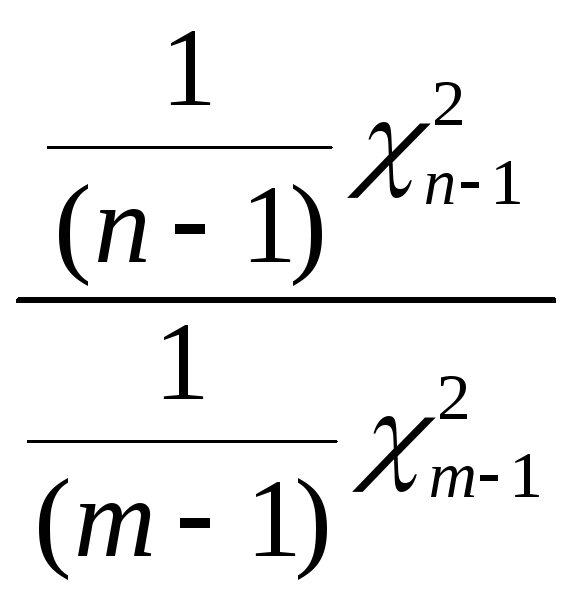где обозначает случайную величину, имеющую распределение . Случайная величина с независимыми и по определению имеет распределение Фишера .

Утверждение доказано.

Распределение Фишера при одновременном возрастании и «концентрируется» в малой окрестности 1, поэтому если гипотеза верна, то значение статистики с большой вероятностью оказывается близким к 1.

Можно показать, что если гипотеза не верна, то есть (пусть для определенности ), то статистика сходится по вероятности к отношению при одновременном возрастании и :

, при .

Таким образом, если гипотеза не верна, то распределение статистики «концентрируется» в окрестности .

Отсюда следует, что в качестве критической области гипотезы следует выбирать те значения статистики , которые «больше 1»:

,

где – квантиль распределения Фишера уровня , где – заданный уровень значимости.