
- •6 .Декодирующее устройство циклического кода для образующего полинома Принцип обнаружения и исправления искажений представить в виде таблицы на примере кодовой комбинации (кл. 2, с. 135-136).
- •7.Мажоритарное декодирующее устройство циклического кода [7, 3], если система проверки для а0 имеет вид:
- •8.Кодирующее устройство циклического кода. Принцип кодирования представить в виде таблицы для образующего полинома и исходной кодовой комбинации (кл. 2, с. 132-133).
- •9. Декодирующее устройство кода Хэмминга [8, 4] с кодовым расстоянием Принцип работы пояснить на примере декодирования кодовой комбинации (кл. 2, с. 126-127).
- •10.Кодирующее устройство кода Хэмминга с кодовым расстоянием Принцип работы пояснить на примере кодирования любой четырехразрядной комбинации (кл. 2, с. 125, 126).
- •12. Квадратурная фазовая манипуляция – кфмп-4 (кл. 5, цифровые виды модуляции).
- •13. Формирователь м-последовательности, соответствующего многочлену с начальными условиями 101. Построить график автокорреляционной функции (кл. 5, формирователь м-последовательности).
- •17. Закодировать сообщение циклическим кодом с (кл. 2, с. 48, 49).
- •19. Амплитудная модуляция
- •20. Частотная модуляция. Спектр сигнала с угловой модуляцией.
- •Спектры сигнала с угловой модуляцией
- •21. Фазоимпульсная модуляция
- •22. Двукратная модуляция ам-чм.
- •23. Потенциальная помехоустойчивость дискретных сообщений.
- •24. Помехоустойчивость передачи непрерывных сообщений.
- •25.Структурные схемы пу и кп системы ти с врк
- •26. Структурные схемы пу и кп цифровой телеметрической системы
- •27. Телеметрические системы с адаптивной дискретизацией
- •28. Телеметрические системы с рациональным построением телеметрического кадра
- •29. Система передачи дискретной информации с рос-ож
- •30. Система передачи дискретной информации с информационной обратной связью и ожиданием (кл. 4, с. 117, 118, 120).
- •31. Квадратичная амплитудная модуляция (кл. 1, цифровые виды модуляции).
- •33. Программная перестройка рабочей частоты (кл. 5, широкополосные сигналы).
1. Рассчитать и построить спектр
периодической последовательности
прямоугольных импульсов амплитудой
 периодом
периодом
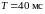 и длительностью
и длительностью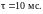 Определить практическую ширину спектра
и среднюю мощность сигнала в этой полосе
частот (сб., пример 1.1).
Определить практическую ширину спектра
и среднюю мощность сигнала в этой полосе
частот (сб., пример 1.1).
Определим скважность импульсов
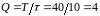 .
.
Частоту следования импульсов находим из выражения
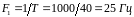
Расчет амплитуд составляющих спектра произведем по выражению

Амплитуда постоянной составляющей
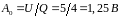 ,
частота
,
частота
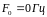 .
.
Амплитуда гармонической составляющей на частоте F1, k=1
 ,
частота 25Гц
,
частота 25Гц
Амплитуда гармонической составляющей на частоте 2F1, k=2
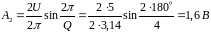 ,
частота 50 Гц
,
частота 50 Гц
Амплитуда гармонической составляющей на частоте 3F1, k=3
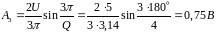 ,
частота 75Гц
,
частота 75Гц
Амплитуда гармонической составляющей на частоте 4F1, k=4
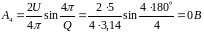 ,
частота 100Гц
,
частота 100Гц
На этом расчет закончим, так как в условии задачи требуется определить практическую полосу частот, которая определяется первым лепестком спектра.
П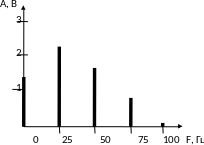 о
полученным данным строим спектр частот
о
полученным данным строим спектр частот
Практическую полосу частот найдем из выражения
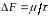 ,
где
,
где
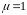 .
.
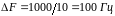
Средняя мощность составляющих, входящих в первый лепесток
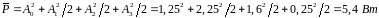
2. Рассчитать и построить амплитудно-частотный
спектр АИМ сигнала и определить
практическую полосу частот, если
амплитуда немодулированных импульсов
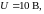 период опроса
период опроса
 длительность информационного импульса
длительность информационного импульса
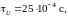 коэффициент глубины модуляции
коэффициент глубины модуляции
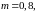 максимальная частота спектра передаваемого
сообщения
максимальная частота спектра передаваемого
сообщения
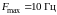 (кл1, с. 39).
(кл1, с. 39).
Определим
скважность импульсов
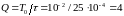
Определим
частоту

Определим максимальную циклическую частоту спектра передаваемого сообщения
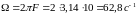
Спектр АИМ-1 сигнала рассчитывается по формуле
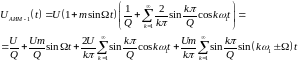
Определим
постоянную составляющую
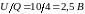
Определим
составляющую на частоте Ω

Определим
составляющие на частотах
 Определим
составляющие на частоте
Определим
составляющие на частоте
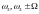
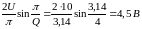
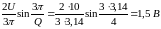

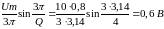
Определим
составляющие на частоте
 Определим
составляющие на частоте
Определим
составляющие на частоте
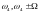
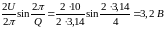

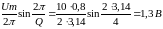
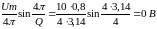
На этом расчет закончим, так как в условии задачи требуется определить практическую полосу частот, которая определяется первым лепестком спектра.
По полученным данным строим спектр частот
 Определим практическую полосу частот
Определим практическую полосу частот
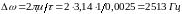 .
.
3. Рассчитать и построить спектр
модулированного по амплитуде сигнала
с частотой несущих колебаний
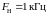 при передаче сигнал с максимальной
частотой
при передаче сигнал с максимальной
частотой
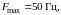 если
амплитуда носителя 10 В, а коэффициент
глубины модуляции
если
амплитуда носителя 10 В, а коэффициент
глубины модуляции
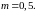 Определить полосу частот и
мощности: молчания, минимальную, среднюю
и максимальную (кл. 1, с. 23, 25).
Определить полосу частот и
мощности: молчания, минимальную, среднюю
и максимальную (кл. 1, с. 23, 25).
Спектр модулированного по амплитуде сигнала определяется по выражению
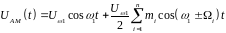
Амплитуда
основной составляющей
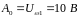 на частоте
на частоте
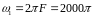
Амплитуды
боковых составляющих
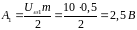 на частотах
на частотах
 и
и
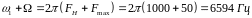 .
.
П о
полученным данным строим спектр частот
о
полученным данным строим спектр частот
Определим полосу частот
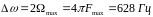
Рассчитаем мощность молчания
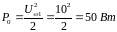
Рассчитаем минимальную мощность
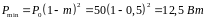
Рассчитаем среднюю мощность
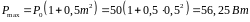
Рассчитаем максимальную мощность
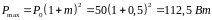
4.
Рассчитать и
построить амплитудно-частотный спектр
АМ-АМ сигнала и определить мощность и
полосу частот, если амплитуда несущей
8 В, частота несущей 10 кГц, частота
поднесущей 200 Гц, коэффициент глубины
модуляции на первой ступени
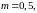 на
второй
на
второй
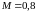 (кл.
1, с. 58).
(кл.
1, с. 58).
Частоту
модулированного сообщения выбираем
исходя из соотношения частот несущей
и поднесущей
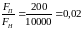 ,
,
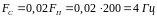
Модулирующее сообщение описывается выражением
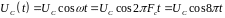
Поднесущая
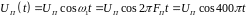
Несущая
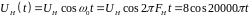
Амплитудно-модулированный сигнал может быть представлен в виде
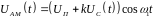 .
.
Получаем
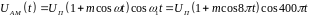
Тогда АМ-АМ сигнал принимает вид
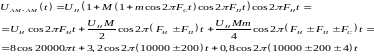
Составляющие на частотах |
Амплитуда, В |
Частота, Гц |
FН |
8 |
10000 |
FН-FП |
3,2 |
9800 |
FН+FП |
3,2 |
10200 |
FН+FП+FC |
0,8 |
10204 |
FН+FП-FC |
0,8 |
10196 |
FН-FП+FC |
0,8 |
9804 |
FН-FП-FC |
0,8 |
9796 |
Спектр АМ-АМ сигнала
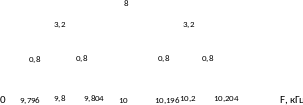
Полоса
частот, занимаемая АМ-АМ сигналом
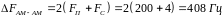
Мощность АМ-АМ сигнала на единичном сопротивлении
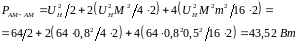
5.Мажоритарное
декодирование циклических кодов.
Составить проверочную матрицу для кода
[7, 3], если образующий полином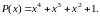 Найти систему проверок для каждого
элемента кодовой комбинации (кл. 2, с.
59-60).
Найти систему проверок для каждого
элемента кодовой комбинации (кл. 2, с.
59-60).
Мажоритарный способ исправления ошибок основан на принятии решения о значении того или иного разряда декодируемой кодовой комбинации по большинству результатов проверок на четность.
Проверки на четность для каждого разряда составляются на основании некоторой матрицы L, которая составляется из проверочной матрицы N путем m-линейных операций над строками.
Находим проверочный полином
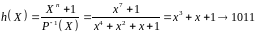
С оставляем
проверочную матрицу. Первая строка
проверочной матрицы циклического кода
есть проверочный полним h(X),
умноженный на
оставляем
проверочную матрицу. Первая строка
проверочной матрицы циклического кода
есть проверочный полним h(X),
умноженный на
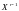 .
Последующие строки проверочной матрицы
есть циклический сдвиг вправо первой.
Число сдвигов равно числу дописанных
справа нулей.
.
Последующие строки проверочной матрицы
есть циклический сдвиг вправо первой.
Число сдвигов равно числу дописанных
справа нулей.
Для построения матрицы L преобразуем матрицу следующим образом. Сложим 2-, 3- и 4-ю строки матрицы
 Аналогично
сложим 1-, 3- и 4-ю строки
Аналогично
сложим 1-, 3- и 4-ю строки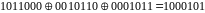
С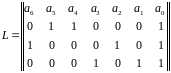 оставим
матрицу L, использовав
для ее построения две полученные суммы
и 4-ю строку проверочной матрицы N:
оставим
матрицу L, использовав
для ее построения две полученные суммы
и 4-ю строку проверочной матрицы N:
Матрица
L дает три независимых
проверочных соотношений с разделенными
относительно члена a0
проверками. Добавив к этим соотношениям
тривиальную проверку
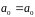 ,
получим систему разделенных относительно
a0 проверок:
,
получим систему разделенных относительно
a0 проверок:
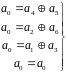
Получим системы проверок для остальных членов

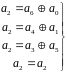
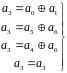
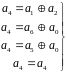
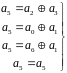
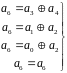
6 .Декодирующее устройство циклического кода для образующего полинома Принцип обнаружения и исправления искажений представить в виде таблицы на примере кодовой комбинации (кл. 2, с. 135-136).
Схема
декодера циклического кода с образующим
полиномом
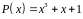
Минимальное кодовое расстояние dmin=3, следовательно код способен исправлять однократные ошибки. Дешифратор синдрома настроен на комбинацию 001.
Работу декодера продемонстрируем в виде таблицы состояний
-
Такт
Вход
Состояние ячеек
Вход дешифратора синдрома DD7
Выход дешифратора синдрома DD7
Выход декодера
DD3
DD5
DD6
0
0
0
0
1
1
1
1
0
110
2
0
0
1
1
000
3
0
1
1
1
101
4
0
1
0
1
001
5
1
0
1
0
011
6
1
1
1
1
100
7
0
1
0
1
001
8
-
1
0
0
011
0
1
9
-
0
1
0
010
0
0
10
-
0
0
1
100
0
0
11
-
1
1
0
111
1
1
12
-
0
1
1
000
0
1
13
-
1
1
1
101
0
1
14
-
1
0
1
001
0
0
Как видно из таблицы, на 10-м такте в ячейках декодирующего регистра сформирована комбинация 001, на 11 такте эта комбинация поступает на вход дешифратора синдрома, на выходе которого возникает сигнал 1. В этот же момент на выходной сумматор поступает искаженный 4-й разряд, который, проходя через сумматор, меняет знак на обратный. Исправленная комбинация имеет вид 1001110.
