(Вопросы, требующие подробного раскрытия):
1)Введение. Физико-химические основы термической диффузии:
Термическая диффузия предназначена для введения примесей в нано –проводник с целью изменения типа его проводимости. Применение терм. диффузии даёт возможность формировать p-n переходы , а также требуемые диффузионные области . При легировании полупроводника атомы примесей , как правило замещают атомы полупроводника в кристаллической решетке:
Термическая диффузия , как правило применяется для формирования p-n перехода. Рассмотрим структуру локального p-n перехода, сформированного в поверхностной области нано проводника:
где О-граница p-n
перехода.
Границей p-n перехода называется линия на которой концентрация вводимой легирующей примеси становится равной концентрации примесей в исходной подложке.
2) Физико-химические основы термической диффузии :
При термической
диффузии примесные концентрации как
правило монотонно убывают при движении
в глубь полупроводника. При проектировании
фотошаблонов необходимо также учитывать
боковую диффузии примеси.(край маски
Si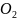
).
Обычно принято считать,что величина
боковой дифракции составляет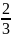
от глубины p-n
перехода. Для формирования диффузионных
областей с электронным типом проводимости
в качестве легирующей примеси обычно
используют фосфор, мышьяк,сульмат. Для
формирования диф.областей с дырочным
типом проводимости обычно используются
бор, галий, индий. Эти примеси наиболее
технологичны, у них хороший коэффицент
диффузии. Для теоретического описания
процессы термической диффузии обычно
используют законы или уравнения Фика.
Первоначально эти законы были выведены
для газов и жидкостей, а затем распространены
на твёрдые кристаллические тела. При
рассмотрении уравнений Фика для простоты
будем учитывать одномерный случай
диффузии и примеси в глубь полупроводника
по оси Х. Первое уравнение Фика связывает
плотность потока лигирующей примеси с
градиентом её концентрации:
J=-D
(1) , где J- плотность потока
течения примеси ; D-коэффицент
диффузии.
«-» - означает , что примесь убывает в глубь проводника. J
Плотность потока
легирующей примеси показывает, сколько
атомов примеси прошло через единицу
площади за единицу времени. N-концентрация
легирующей примеси. N[
],
х-константа, х[см],
D[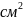
.
].
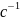Коэффицент диффузииии D
экспоненциально возрастает с ростом
температуры .
D=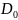
.exp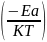
(2) , где: К-постоянная Больцмана;
Т-собственная температура в кельвинах;
Ea-энергия активации
диффузионного процесса;
-коэффецент,зависящий
от типа подложки, кристаллографической
ориентации поверхности, вида легирующей
примеси и некоторых других факторов.
Для практического использования
необходимо определить профиль
распределения легирующей примеси
N(х,t).
Рассмотрим термическую диффузию
,протекающую через единичную площадь
полупроводника:
Тогда приращение
атомов примеси в атоме примеси в N
будет равнятся: ӘNx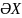
=-ӘJӘt.
=-
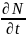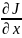(3).
Из (1) и (3) получим
уравнение Фика:
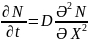. С точки зрений микро и нано электроники
наибольшей интерес представляет решение
уравнения (4) для следующих двух граничных
условий :
l. Легирование из неограниченного источника примеси;
ll.Легирование из ограниченного источника примеси ;
Рассмотрим эти случаи более подробно :
1)Неограниченный
источник примеси: В этом случае во время
всего процесса термической диффузии
на поверхности полупроводника присутствует
неограниченный источник примеси с
концентрацией
.
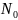Решение ур-ия (4) имеет следующий вид :
N(x,t)=
.erfc
(5)
, где erfc-функция
ошибок,T-температура
изотермического режима,
= const во время процесса
диффузии . erfc(V)=(-F).
2)Ограниченный источник
примеси: В этом случае решение
дифференциального уравнения второго
закона Фика будет иметь следующий вид:
N(x,t)=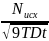
. ехp
(6)
В технологии микроэлектроники легирование из неограниченного источника примеси часто называют загонкой примеси, и используют на начальном этапе формирование p-n перехода. Легирование из ограниченного источника примеси является обычно второй заключительной стадией формирования p-n перехода и в технологии получило название разгонка-примесь. Разгонка примесь даёт возможность сформировать резкий p-n переход.