Однофазный трансформатор

Цель работы: изучить устройство и принцип действия однофазного трансформатора, испытать его в режимах холостого хода, короткого замыкания и нагрузки, рассчитать параметры схемы замещения.

1. Принцип действия однофазного трансформатора

На рис. 1 схематично изображен однофазный понижающий трансформатор, имеющий обмотку ВН с числом витков W₁ и обмотку НН с числом витков W₂. вторичная обмотка разомкнута (режим хх), а к первичной обмотке подведено напряжение сети U₁.

Р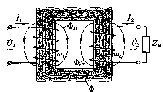 ис.1

При подведении к обмотке ВН напряжения сети в ней потечет ток I₁, который создаст магнитодвижущую силу (МДС)

F₁ = I₁*W₁

МДС F₁ формирует магнитный поток Ф₁, основная часть которого замыкается по магнитопроводу (Ф₀), и значительно меньшая часть замыкается по воздуху (Ф_1S)

(в реальных силовых трансформаторах Ф₀ = 0,95-0,96 Ф₁)

Согласно закону электромагнитной индукции (е = ) основной магнитный поток Ф₀, сцепляясь с витками обмотки ВН, наводит в ней ЭДС самоиндукции, действующее значение которой равно Е₁ , и, пересекаясь с витками обмотки НН, наводит в ней ЭДС с действующим значением Е₂ . Магнитный поток Ф_1S, сцепляясь с витками обмотки ВН, наводит в ней ЭДС рассеяния, действующее значение которой равно Е_1S.

Таким образом, при разомкнутой обмотке НН под действием напряжения U₁ (в обмотке с числом витков W₂) наводится ЭДС Е₂, которая используется для питания нагрузки Z_н вторичной цепи трансформаторов.

Из теории электрических цепей имеем:

Е 1S = - jI1 X1	(1)
E1 = 4,44 W1 f1 Ф	(2)
E2 = 4,44 W2 f1 Ф	(3)
Z 1 = R1 + j X1	(4)
Z 2 = R2 + j X2	(5)

где f₁– частота напряжения сети;

Z ₁ , Z ₂ – комплексы полных сопротивлений обмоток ВН и НН трансформатора;

R₁, R₂, – активные, X₁, X₂ – индуктивные сопротивления рассеяния обмоток ВН и НН трансформатора.

Количественная оценка уровней напряжения обмоток ВН и НН трансформатора осуществляется коэффициентом трансформации

K = = ≈

(6)

где U_1н , U₂₀ – напряжения обмоток ВН и НН в режиме хх (U₂₀ = Е₂).

Согласно второму закону Кирхгофа в установившемся режиме можно записать следующее уравнение электрического равновесия обмотки ВН

U₁ + Е₁ + Е_1S = I₁ R

На практике пользуются уравнением

U1 = - Е1 + I1 R + jI1 X1

(7)

2. Режим нагрузки трансформатора

При замыкании обмотки НН на нагрузку в цепи этой обмотки возникает ток I₂, который создаст МДС

F₂ = I₂ W₂

МДС F₂ размагничивает магнитопровод при индуктивной нагрузке и подмагничивает его при емкостной.

Режим нагрузки трансформатора характеризуется соотношением токов I₁, I₀ и I₂. Если учесть, что при работе трансформатора в пределах номинальной нагрузки его магнитопровод ненасыщен и сделать следующее допущение

U₁ ≈ Е₁ = const,

то, используя формулу (2), можно записать условие:

Ф0 = ≈ = const,

(8)

суть которого заключается в том, что при изменении тока нагрузки I₂ от нуля до номинального значения основной магнитный поток Ф₀ остается неизменным (не зависит от нагрузки).

Условие (8) может быть выполнено в том случае, если справедливо равенство:

F₀ = F₁ + F₂ = const,

или

I0W1 = I1 W1 + I2 W2 = const

(9)

Разделив обе части уравнения (9) на величину W₁ , получим уравнение токов трансформатора, работающего в режиме нагрузки:

I0 = I1 + I2

(10)

Обозначив I₂ = I₂ = I₂′ – ток вторичной обмотки, приведенный к числу витков первичной обмотки, и решив последнее уравнение относительно тока I₁, запишем уравнение токов в окончательном виде

I1 = I0 + (- I2′)

(11)

Из уравнения (11) следует, что при работе трансформатора под нагрузкой условие (8) выполняется за счет изменения тока I₁ в пределах, строго соответствующих диапазону изменения тока нагрузки I₂′ .