§ 3. Картографические проекции и сетки

Картографической проекцией называется всякий способ изображения сфероида (или шара) на плоскости, при котором каждой точке М изображаемой поверхности соответствует взаимно-однозначная точка М' на плоскости, называемая ее изображением; непрерывному пере­мещению точки М соответствует непрерывное перемещение точки М'.

Положение точки М может быть задано в различных системах коорди­нат с соответствующими системами координатных линий.

Координатными линиями называются геометрические места точек, имеющих одну из координат постоянной. В частности, координатными линиями являются меридианы и параллели.

Изображение системы координатных линий в проекции называется картографической сеткой.

Основой для построения карт является картографическая сетка, изобра­жающая координатные линии той системы, в которой даются изображаемые точки опорной сети на земной поверхности: обычно географической системы, часто — общегосударственной системы плоских прямоугольных координат.

На шаре (но не на сфероиде) (рис. 1) любая точка Z может быть взята за полюс системы координат совершенно аналогичной географической.

Различные системы координатных линий изобразятся в данной проекции сетками различного вида. Та сетка, которая имеет самый простой вид из всех, свойственных данной проекции, носит название нормальной (прямой) сетки этой проекции. Наоборот, та система, координатные линии которой изображаются в виде нормальной сетки, называется нормальной системой координат. По аналогии с географическими координатами, координаты в нормальной системе также называют широтами и долготами, оговаривая, в какой именно системе.

Если полюс Z нормальной системы координат совмещен с полюсом Р изображаемой (географической) системы, координатные линии обеих систем сливаются, и географические меридианы и параллели изображаются в про­екции в виде нормальной сетки.

Если дуга PZ на шаре равна 90°, изображение географических мери­дианов и параллелей имеет вид поперечной сетки.

В общем случае, если 0 < PZ < 90°, изображение географических мери­дианов и параллелей имеет вид косой сетки.

Соответственно сказанному о расположении полюса Z относительно полюса Р говорят о применении проекций в нормальном, поперечном или косом положении или иначе о полярной, экваториальной или горизонтальной (горизонтной) про­екциях и сетках.

В общем случае картографическая проекция определяется уравнениями, выражающими плоские прямоугольные (х, у) или полярные (w, р) коорди­наты изображения точки М' в функции от пространственных /г, а или по­верхностных X, Y координат изображаемой точки М в нормальной системе.

Эти уравнения имеют вид:

х — f₁(h, а) = F₁(X, У); = Ф₁(h , а)

y = f₂(h , а) = F₂(X, Y)\ =Ф₂(h , а)

Рис. 1. Связь между коорди­натами в географической и нормальной системах координат

)

Аналитическому заданию проекции уравнениями типа (1) соответст определенный вид нормальной картографической сетки данной проекции. Общая теория искажения

Картографическая проекция может быть определена (задана) не только аналитически уравнениями типа, но и законом построения нормальной сетки проекции, например видом географических меридианов и параллелей для проекции в нормальном положении. Такому способу задания соответ­ствуют определенные уравнения типа (1).

Иногда картографическая проекция может быть определена законом перспективного переноса точек изображаемой поверхности н а плоскость или на вспомогательную поверхность конуса или цилиндра.

Проекции могут применяться как для изображения всей земной поверх­ности, так и для изображения отдельных ее частей. Крупномасштабные склейки больших размеров не удобны для пользования; практически прихо­дится пользоваться отдельными листами карт или склейками небольшого числа листов. Поэтому не имеет практического значения, может или не мо­жет быть склеена без разрывов сплошная карта из неограниченного числа листов. Отсюда получили распространение крупномасштабные карты в мно­гогранных проекциях.

В многогранных проекциях на отдельных листах карты изоб­ражаются отдельные трапеции земной поверхности, образованные меридиа­нами и параллелями определенной частоты. Изображение трапеций на кар­тах может выполняться в любой проекции.

Благодаря некоторой растяжимости бумаги, 4 и даже 9 листов карты в масштабе

1 : 1 ООО ООО, составленной в многогранной проекции, можно склеить вместе в сплошную карту. С увеличением масштаба число листов сплошной склейки возрастает.

ОБЩАЯ ТЕОРИЯ ИСКАЖЕНИЯ

Карта есть изображение земной поверхности в переменном масштабе. Масштаб изображения может меняться от точки к точке и по различным направлениям из точки проекции.

Масштаб в данной точке проекции по данному направлению носит название частного масштаба.

Масштаб подписанный на карте, носит название главного или общего масштаба карты. Он представляет собой некоторый средний масштаб в пре­делах карты, соблюдаемый в некоторых точках или по некоторым линиям, которые обыкновенно указываются вместе с главным масштабом.

Частный масштаб и увеличение — величины взаимно пропорциональные, поэтому соответствующие им понятия часто заменяют одно другое: частный масштаб берется по отношению к натуральным размерам, а увеличение — по отношению к размерам, уменьшенным в главном масштабе. Уклонение v увеличения с частного масштаба от единицы есть искажение длин в данной точке по данному направлению.

ГОСУДАРСТВЕННАЯ ОПОРНАЯ СЕТЬ

Государственная опорная сеть СССР представляет систему пунктов, определенных в единой системе коор­динат и надежно закрепленных на местности. Она яв­ляется основой для всех геодезических и топографиче­ских работ, служащих целям народного хозяйства и обороны страны.

Создание топографической карты, равноточной во всех ее частях на огромной территории страны, возможно только при наличии государственной сети опорных точек. Опорные сети исключает возмож­ность накопления ошибок измерений в какой-либо одной части снимаемой территории и тем самым обес­печивают необходимую, наперед заданную точность съемочных работ на всей территории страны.

Необходимость создания опорных сетей определяет­ся также тем, что топографические работы ведут в раз­ное время и на различных частях огромных

пространств. Для строгого учета и систематизации съемок территорию делят на отдельные съемочные трапеции, границы которых должны быть точно определены на местности.

Опорная сеть высших классов служит также для определений формы и размеров Земли.

Плановое положение опорных пунктов определяется методами триангуляции и полигонометрии; высоты—ме­тодами геометрического и геодезического (тригономе­трического) нивелирования.

Точность опорной сети определяется требованиями, предъявляемыми к ней самым круглым масштабом го­сударственной топографической съемки..

«Основные положения о государственной геодезиче­ской сети СССР» предусматривают создание государ­ственной опорной сети, которая по своей густоте и точ­ности должна обеспечить возможность геодезического обоснования сплошных топографических съемок мас­штаба 1 : 5000 и крупнее.

Метод триангуляции заключается в построении на местности системы треугольников. В которых измеряют все углы и одну из сторон, называемую выходной; путем вычислений получают длину сторон всех тре­угольников и координаты их вершин.

Непосредственное измерение выходной стороны не всегда возможно из-за условий местности. В таких случаях измеряют линию а—b, называемую базисом, которую связывают с выходной стороной 1—2 при по­мощи вспомогательной триангуляции, называемой ба­зисной сетью (1— а — 2— b ) (рис. 1).

Триангуляционные сети подразделяют по точности на 1, 2, 3 и 4 классы, 1 и 2 разряды.

Триангуляция 1 класса используется в научных исследованиях, связанных с определением фигуры и размеров Земли, а также является основой триангуляции (полигонометрии) последующих клас­сов.

Триангуляцию I класса строят в виде рядов треугольников,реже четырех­угольников и центральных систем, расположенных вдоль меридианов и парал­лелей и образующих замкнутые полигоны периметром до 800 км (рис. 2).

Ряды триангуляции I класса составляют звенья, со­стоящие из цепи треугольников, близких к равносторон­ним со средней длиной сторон 20—25 км.

Рис. 1. Схема треуголь­ников

На концах звена Триангуляции 1 класса опреде­ляют длину выходных сторон непосредственным изме-

Рис. 2. Схема государственной триангуляции

рением или из базисных сетей с ошибкой не более 1:350 000 и производят астрономические наблюдения, включающие измерение азимутов.

Триангуляция II к л а с с а — геодезическая основа для развития триангуляции III и IV классов, она строится в виде сплошных сетей, заполняющих территорию, ограниченную первоклассным полигоном.

Дальнейшим развитием государственной сети явля­ются сети

т р и а н гуля ц и и III и IV к л а с с о в.

Длины выходных сторон сети II класса определяют­ся из непосредственных измерений или из базисных се­тей с относительной ошибкой не более

1 :250 000.

Базисы в триангуляции II класса располагаются так, что любая сторона сети может быть получена в результате решения не более шести-семи треуголь­ников.

Пункты триангуляции III и IV классов определяют­ся вставками систем или отдельных пунктов относи­тельно пунктов триангуляций высших классов.

Таблица 1 Технические показатели триангуляции

1 Класс триан­гуляции	Длина сторон, км	Относительная ошибка изме­рения выход­ной стороны	Средняя квадратическая ошибка измерения угла, сек.	Предельные допустимые невязки тре - угольника, сек.
I	20—25	1 : 350 000	± 0,7	± 2,5
II	13	1 : 250 000	± 1,0	± 3,5
III	8		± 1,5	± 5,0
IV	1,5-6		± 2,0	± 7,0

Работы по проложению сетей триангуляции I, II и III классов ведут: Главное управление геодезии и кар­тографии, Военно-топографическое управление и Гидро­графическое управление ВМС.

Работы по проложению, сетей триангуляции IV клас­са выполняют учреждения, производящие топографиче­скую съемку масштаба 1 : 5000 и крупнее.

Пункты государственной триангуляции закрепляют­ся на местности надежными подземными сооружения­ми—центрами .

Видимость между пунктами обеспечивается возведе­нием над центрами наземных сооружений — Пирамид или сигналов .

Метод точной полигоиометрии применяют для созда­ния опорной сети в равнинных, залесенных и пустынно- степных районах.

Точную полигонометрию подразделяют на траверсы с непосредственным измерением линий и параллактическую полигонометрию с определе­нием длины сторон косвенным путем по измеренному базису и вспомогательным углам .

Длина сторон полигонометрии 200—3000 м; парал­лактические базисы выбирают длиной, кратной 24 м; измеряют их инварными проволоками.

Точки полигонометрии закрепляют на местности центрами и марками .

Для обеспечения видимости между пунктами над центрами устанавливают пирамиды.

Государственная нивелирная сеть является высотной основой топографических съемок всех масштабов и геодезических измерений. По точности и назначению нивелирную сеть разделяют на I, II, III и IV классы.

Высота их пунктов вычисляется от нуля Кронштадского футштока. Нивелирная сеть I и II классов является главной высотной, посредством которой устанавливается единая система высот на всей территории РФ, а также используются в научных исследованиях.

Нивелирные сети III и IV классов служат высотной основой для топографических съемок и решения инженерных задач.

Нивелирные линии I класса прокладывают по направлениям, указанным в «Основных положениях» 1954 г. и выполняют с точностью, характеризующейся средней квадратической случайной ошибкой

η = 0,5 мм. и систематической δ = ± 0,05 мм. на 1 км. хода. Нивелирные ходы I и II классов прокладывают вдоль шоссейных, железнодорожных дорог и других улучшенных путей сообщения.

Нивелирная сеть II класса прокладываются в виде линий, опирающихся на пункты нивелирования I класса и образующих полигоны периметром

500- 600км.с точностью, обеспечивающей получение невязок превышений полигонов не более 5 мм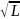 ( - длина хода в километрах).

Нивелирование сети III класса развивается внутри полигонов нивелирования II класса, образуя полигоны периметром 150-200 км. Каждый полигон II класса ходами III класса делится на 8-9 частей. Допустимая невязка прямого и обратного ходов нивелирования III класса не должна превышать величины 10 мм .

Внутри полигонов III класса прокладывают ходы нивелирования

IV класса, невязка последних должна быть не более 20 мм . По абсолютной величине.

СГУЩЕНИЕ ГОСУДАРСТВЕННОЙ СЕТИ ОТ ОБЩЕГО К ЧАСТНОМУ

( IVкласса, 1-го и 2 разрядов) методами: триангуляции; полигонометрии, трилатерации; сети сгущения; сети геометрического нивелирования.

Создание маркшейдерско-геодезических сетей методом полигонометрии

Полигонометрия применяется для сгущения пунктов плано­вых сетей в тех случаях, когда и организационно и по технико- экономическим показателям она выгоднее построения триангуля­ции 4 класса, 1 и 2 разрядов. Возможность применения совре­менных средств измерения длин и хорошая приспособляемость «Условиям местности делают полигонометрию весьма гибким методом построения маркшейдерско-геодезических сетей. Действующими инструкциями к полигонометрии 4 класса, 1 и 2 разрядов предъявляются требования, приведен­ные в табл. 7.

Полигонометрические работы имеют следующие стадии:

1) составление проекта;

2) рекогносцировка трассы и пунктов поворота полигонометрического хода;

3) расстановка и закладка центров;

4) исследование инструментов, угловые и линейные измере­ния;

привязка;

5) привязка;

6) обработка результатов полевых измерений и оценка их точности;

7)предварительные вычисления;

8. уравнивание;

9) вычисление окончательных значений длин линий, дирекционных углов и координат;

10) оценка точности полученных результатов;

11) составление отчета.

11) составление отчета.

Полигонометрия строится в виде отдельных ходов или систем, опирающихся на исходные пункты. Отдельные ходы могут быть замкнутыми или разомкнутыми. Замкнутый ход или полигон опирается на один исходный пункт с известными координатами и примыкает к исходным направлениям.

Разомкнутый ход опирается концами на исходные пункты и примыкает к исходным направлениям. Для контроля и большей жесткости рекомендуется на каждом исходном пункте примыкать ходом к двум исходным направлениям. Различают ломаные и вытянутые разомкнутые ходы. Ломаные ходы по сравнению с вытянутыми имеют большую протяженность и большее число углов поворота, что приводит к увеличению объема полевых работ и к менее точному определению координат пунктов полигонометрии. Поэтому во всех случаях, когда это возможно, следует прокладывать вытянутые полигонометрические ходы с примерно равными сторонами.

Таблица 7

Показатели	Полигонометрии
	4 класса	1 разряда	2 разряда
Предельные длины ходов, км	10	5	3
Периметры полигонов, образованные полигонометрическими ходами в сво­бодных сетях (км), ие более	30	15	9
Длины сторон хода, км	0,25—0,8	0,12-0,6	0,08-0,3
Длина ход а от узловой точки до пункта высшего класса или разряда (км), не более	7	3	2
Число сторон в ходе, не более	15	15	15
Относительная невязка хода, ие более	1:25000	1:10000	1 :5000
Средняя квадратическая погрешность измеренного угла по невязкам в поли­гонах, не более	2"	5"	10"
Угловая невязка хода или полигона	5"√n	10"√n	20 "√n

Ход можно считать вытянутым, если направления его сторон отклоняются от направления замыкающей в пределах 24°, а вершины хода отклоняются в обе стороны от линии, проведенной через центр тяжести параллельно замыкающей хода, не более чем на 1,/8 длины замыкающей [92].

В случае если два одиночных хода с допустимыми длинами сторон окажутся проложенными близко один к другому, то их следует связать, проложив ход между их средними точками, так как именно середина хода нуждается в укреплении.

Для ослабления влияния погрешностей угловых измерений в полигонометрических ходах большой протяженности и с большим числом углов поворота следует предусматривать определение для одной из линий, расположенной примерно в середине хода (рис. 10), дирекционного угла путем передачи с пунктов триангуляции или определять его астрономическим путем . При составлении проекта полигонометрической сети необхо­димо учитывать особенности производства разбивочных работ

Рис. 10. Полигонометрический ход с промежуточным дирекциониым углом

при обустройстве месторождений, а также допустимые длины теодолитных ходов, прокладываемых между пунктами полигонометрии в качестве обоснования для съемок различного масштаба.

Для ходов с большим числом сторон и значительно отличающихся от вытянутых необходимо производить предвычисление ожидаемой точности.

Топогеодезический раздел. Одной из основных задач маркшейдерской службы на открытых горных разработках является создание геометрической основы съемочных работ в виде маркшейдерской опорной сети. Организация на территории своей производственно-хозяйственной деятельности в дополнение к геодезической сети создает маркшейдерскую опорную сеть. Маркшейдерские опорные сети могут создаваться с использованием спутниковой аппаратуры. Виды создания опорных геодезических сетей.Маркшейдерские опориые сети на земной поверхности создаются методами триангуляции, трилатерации, полигонометрии 4 классов, 1 и 2 разрядов, нивелированием III и IV классов в соответствии с установленными требованиями. Метод триангуляции. Триангуляция (от лат. triangulum - треугольник), один из методов создания сети опорных геодезических пунктов и сама сеть, созданная этим методом; состоит в построении рядов или сетей примыкающих друг к другу треугольников и в определении положения их вершин в избранной системе координат. В каждом треугольнике измеряют все три угла, а одну из его сторон определяют из вычислений путём последовательного решения предыдущих треугольников, начиная от того из них, в котором одна из его сторон получена из измерений. Если сторона треугольника получена из непосредственных измерений, то она называется базисной стороной триангуляции. В прошлом вместо базисной стороны непосредственно измеряли короткую линию, называемую базисом, и от неё путём тригонометрических вычислений через особую сеть треугольников переходили к стороне треугольника триангуляции. Эту сторону триангуляции обычно называют выходной стороной, а сеть треугольников, через которые она вычислена,- базисной сетью. В рядах или сетях триангуляции для контроля и повышения их точности измеряют большее число базисов или базисных сторон, чем это минимально необходимо.Триангуляция служит для:определения фигуры и размеров Земли методом градусных измерений;изучения горизонтальных движений земной коры;обоснования топографических съёмок в различных масштабах и целях;обоснования различных геодезических работ при изыскании, проектировании и строительстве крупных инженерных сооружений, при планировке и строительстве городов и т.д.

При построении триангуляции исходят из принципа перехода от

общего к частному, от крупных треугольников к более мелким. В связи с

этим триангуляция подразделяется на классы, отличающиеся точностью

измерений и последовательностью их построения. В малых по территории

странах триангуляция высшего класса строят в виде сплошных сетей

треугольников. В государствах с большой территорией (Россия, Канада, КНР,

США и др.) триангуляцию строят по некоторой схеме и программе.

Наиболее стройная схема и программа построения триангуляции

применяется в России.

Государственная триангуляция делится на 4 класса. 1-го класса

строится в виде рядов треугольников со сторонами 20-25 км, расположенных

примерно вдоль меридианов и параллелей и образующих полигоны с

периметром 800-1000 км. Углы треугольников в этих рядах измеряют

высокоточными теодолитами. В местах пересечения рядов триангуляции 1-го

класса измеряют базисы при помощи мерных проволок (см. Базисный

прибор), причём погрешность измерения базиса не превышает 1; 1000000

доли его длины, а выходные стороны базисных сетей определяются с

погрешностью около 1: 300 000. После изобретения высокоточных

электрооптических дальномеров стали измерять непосредственно базисные

стороны с погрешностью не более 1: 400 000. Пространства внутри

полигонов триангуляции 1-го класса покрывают сплошными сетями

треугольников 2-го класса со сторонами около 10-20 км, причём углы в них

измеряют с той же точностью, как и в триангуляции 1 -го класса. В сплошной

сети триангуляции 2-го класса внутри полигона 1 -го класса измеряется также

базисная сторона с указанной выше точностью. На концах каждой базисной

стороны в триангуляции 1-го и 2-го классов выполняют астрономические определения широты и долготы, а также азимута. Кроме того, астрономические определения широты и долготы выполняют и на промежуточных пунктах рядов триангуляции 1-го класса через каждые примерно 100 км, а по некоторым особо выделенным рядам и значительно чаще. На основе рядов и сетей триангуляции 1-го и 2-го классов определяют пункты триангуляции 3-го и 4-го классов, причём их густота зависит от масштаба топографической съёмки. Например, при масштабе съёмки 1: 5000 один пункт триангуляции должен приходиться на каждые 20-30 км².

Пункты триангуляции в целях долговременной их сохранности на местности закрепляются закладкой в грунт особых устройств в виде металлических труб или бетонных монолитов с вделанными в них металлическими марками, фиксирующими положение точек, для которых даются координаты в соответствующих каталогах. Координаты пунктов триангуляции определяют из математической обработки рядов или сетей триангуляции. При этом реальную Землю заменяют некоторым референц- эллипсоидом, на поверхность которого приводят результаты измерения углов и базисных сторон триангуляции. В России принят референц-эллипсоид Красовского.

Построение триангуляции и её математическая обработка приводят к созданию на всей территории страны единой системы координат, позволяющей ставить топографо-геодезические работы в разных частях страны одновременно и независимо друг от друга. При этом обеспечивается соединение этих работ в одно целое и создание единой общегосударственной топографической карты страны в установленном масштабе.