
Задание 3
Газета "Нихон кэйдзай симбун" провела "Обследование торговых центров за 1984 год", в частности универмагов, супермаркетов и других предприятий розничной торговли и опубликовала перечень объемов продаж. В табл. приведены результаты обследования для 20 наиболее крупных универмагов.
Установить имеется ли связь между площадью и объемом продаж? Построить линию регрессии зависимости объема продаж от торговой площади. Сравнить одно из истинных значений с предсказанным.
Объем продаж для крупных торговых центров за 1984 г.
Место |
Центры, торгующие в рассрочку |
Объем продаж, млн. иен |
Торговая площадь, тыс. м2 |
1 |
Такасамия (токио) |
124 |
76 |
2 |
Мицукоси, главный магазин (Токио) |
180 |
29 |
3 |
Ханкю хяккатэн, главный магазин (Осака) |
80 |
57 |
4 |
Исэтан, главный магазин в Синдзюку (Токио) |
105 |
67 |
5 |
Даймару, Осака — Синсайбаси |
142 |
40 |
6 |
Такасимая (Осака) |
162 |
30 |
7 |
Токю хяккатэн. главный магазин (Токио) |
131 |
40 |
8 |
Мацудзакая (Нагоя) |
177 |
76 |
9 |
Сого (Кобэ) |
79 |
38 |
10 |
Хансин хяккатэн (Осака) |
90 |
69 |
11 |
Мацудзакая. Уэно (Токио) |
94 |
26 |
12 |
Такасимая (Киото) |
185 |
71 |
13 |
Даймару (Киото) |
147 |
24 |
14 |
Даймару (Токио) |
192 |
57 |
15 |
Сого (Осака) |
61 |
30 |
16 |
Мэтэцу хяккатэн (Аити) |
152 |
26 |
17 |
Даймару (Кобэ) |
131 |
69 |
18 |
Иватая, главный магазин (Фукуока) |
65 |
31 |
19 |
Мацуя, главный магазин на Гиндзе (Токио) |
186 |
47 |
20 |
Маруэй (Аити) |
178 |
76 |
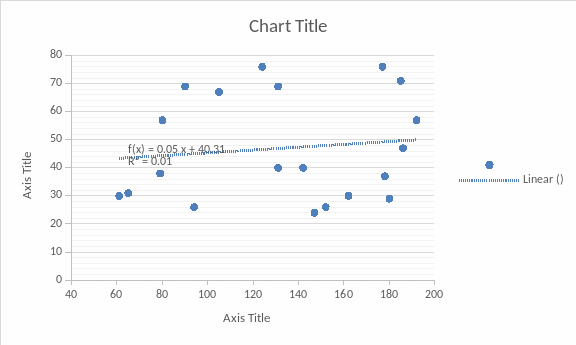
Видно, что точки не выстраиваются на условной наклонной или восходящей линии, можно сказать, что не имеется зависимости (корреляции), т.е. увеличение торговых площадей не приводит к увеличению объема продаж.
Наглядная оценка диаграммы носит предварительный характер. Для более точной оценки зависимости проводится математическая обработка массива парных данных, которая дает численное значение коэффициента корреляции r. Этот математический метод определения корреляции между анализируемыми параметрами называется корреляционным анализом.
Коэффициент корреляции позволяет количественно определить силу линейной связи между x и y. Коэффициент корреляции вычисляется в соответствии со следующими формулами:

Коэффициент корреляции (r) принимает значения из диапазона -1 ≤ r ≤ 1.
Таблица 1
Данные для определения коэффициента корреляции
Значения Х |
Значения Y |
хi-хср |
уi-уср |
(хi-хср)2 |
(yi-yср)2 |
(хi-хср)(yi-yср) |
2 |
43 |
-0,37 |
-1,933 |
0,137 |
3,736 |
0,715 |
135 |
32 |
13,65 |
-18,6 |
186,323 |
345,96 |
-253,89 |
45 |
40 |
-76,35 |
-10,6 |
5829,32 |
112,36 |
809,31 |
53 |
60 |
-68,35 |
9,4 |
4671,72 |
88,36 |
-642,49 |
76 |
63 |
-45,35 |
12,4 |
2056,62 |
153,76 |
-562,34 |
141 |
43 |
19,65 |
-7,6 |
386,123 |
57,76 |
-149,34 |
153 |
49 |
31,65 |
-1,6 |
1001,72 |
2,56 |
-50,64 |
209 |
44 |
87,65 |
-6,6 |
7682,52 |
43,56 |
-578,49 |
141 |
49 |
19,65 |
-1,6 |
386,123 |
2,56 |
-31,44 |
127 |
50 |
5,65 |
-0,6 |
31,9225 |
0,36 |
-3,39 |
191 |
60 |
69,65 |
9,4 |
4851,12 |
88,36 |
654,71 |
193 |
74 |
71,65 |
23,4 |
5133,72 |
547,56 |
1676,61 |
77 |
50 |
-44,35 |
-0,6 |
1966,92 |
0,36 |
26,61 |
113 |
36 |
-8,35 |
-14,6 |
69,7225 |
213,16 |
121,91 |
148 |
73 |
26,65 |
22,4 |
710,223 |
501,76 |
596,96 |
94 |
23 |
-27,35 |
-27,6 |
748,023 |
761,76 |
754,86 |
170 |
26 |
48,65 |
-24,6 |
2366,82 |
605,16 |
-1196,79 |
100 |
60 |
-21,35 |
9,4 |
455,823 |
88,36 |
-200,69 |
106 |
39 |
-15,35 |
-11,6 |
235,623 |
134,56 |
178,06 |
58 |
79 |
-63,35 |
28,4 |
4013,22 |
806,56 |
-1799,14 |
97 |
62 |
-24,35 |
11,4 |
592,923 |
129,96 |
-277,59 |
2427 |
1012 |
1,14E-13 |
-2,8E-14 |
43376,55 |
4684,8 |
-927,2 |
|
|
|
|
|
|
|
хср= |
121,35 |
|
|
|
|
|
уср= |
50,6 |
|
|
|
|
|
Коэффициент корреляции:
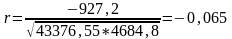
Значение r, очень далеко от -1, следовательно, подтверждается отсутствие корреляции.
