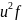Содержание
Задание 1…………………………………………………………………………..3
Задание 2…………………………………………………………………………..6
Задание 3…………………………………………………………………………10
Задание 4…………………………………………………………………………14
Список литературы………………………………………………………………19
Задание 1
Приводимая ниже таблица является результатом 60 наблюдений.
-
305.05
302.60
307.49
303.06
304.23
313.31
311.58
311.67
306.24
303.38
304.15
307.47
305.89
306.47
310.18
309.26
310.45
302.67
309.48
310.08
304.25
303.96
309.22
301.22
305.96
312.23
306.67
307.36
309.76
308.03
303.92
305.20
309.83
310.80
300.54
313.73
307.92
304.17
313.33
300.63
304.33
305.09
307.59
300.48
303.77
308.07
311.43
304.70
301.22
308.70
312.30
300.28
307.81
306.82
302.12
302.54
302.13
301.00
309.68
313.08
а) Подготовьте данные для построения гистограммы, разбив их на не менее 6 классов.
b) вычислите средние значения и стандартное отклонение, используя табличный метод.
c) определите предельные значения, в которых находится примерно 95% результатов наблюдений.
d) Нарисуйте гистограмму и нанесите на нее средние значение и плюс-минус три стандартных отклонения от среднего значения.
Решение:
Определим число выполненных изменений: n = 60.
Определим интервал между наибольшим и наименьшим числовым значением диаметров осей: R = 313.73 – 300.28 = 13.45.
В
зависимости от числа данных весь интервал
R
делится на классы k.
.
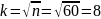Определим
ширину h
каждого класса
=
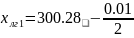300.275
Занесем данные в контрольный листок.
Класс |
Границы интервалов |
Поле регистрации данных |
Частота |
1 |
300.275÷301.955 |
\\\\\\\ |
7 |
2 |
301.955 ÷303.635 |
\\\\\\\ |
7 |
3 |
303.635÷305.315 |
\\\\\\\\\\\\ |
12 |
4 |
305.315÷306.995 |
\\\\\\ |
6 |
5 |
306.995÷308.675 |
\\\\\\\\ |
8 |
6 |
308.675÷310.355 |
\\\\\\\\\ |
9 |
7 |
310.355÷312.035 |
\\\\\ |
5 |
8 |
312.035÷313.715 |
\\\\\\ |
6 |
b)
Рассчитаем среднее значение изучаемого
параметра и
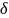табличным способом
№ |
|
f |
u |
uf |
|
1 |
301.615 |
7 |
-2 |
-14 |
28 |
2 |
302.795 |
7 |
-1 |
-7 |
7 |
3 |
304.510 |
12 |
0 |
0 |
0 |
4 |
306.155 |
6 |
1 |
6 |
6 |
5 |
307.835 |
8 |
2 |
16 |
32 |
6 |
309.515 |
9 |
3 |
27 |
81 |
7 |
311.195 |
5 |
4 |
20 |
80 |
8 |
312.875 |
6 |
5 |
30 |
150 |
Итого |
|
60 |
|
108 |
384 |
=1.68
3.007
Определим предельные значения, в которых находится примерно 95% результатов наблюдения:
95%
наблюдений находятся в пределах
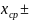2
2 = [301.520;313.5548]
Построим гистограмму.
Таким образом можно сделать вывод, что процесс является управляемым так как гистограмма полностью попадает в интервал 3